牛客练习赛40F(一对约束，只选一个有额外代价，都选有额外代价，不选有额外代价)

题：https://ac.nowcoder.com/acm/contest/369/F

题意：n支代价为w[i]的剑，m个约束，[x,y,v0,v1,v2]同时选加上v0的额外贡献，都不选加上v1的额外贡献，只选一个减去v2的额外贡献，求最大贡献

分析：考虑总体减去最小贡献(最小割)

　　　单考虑一对约束和源点汇点关系，建立经典模型：

 

 

 

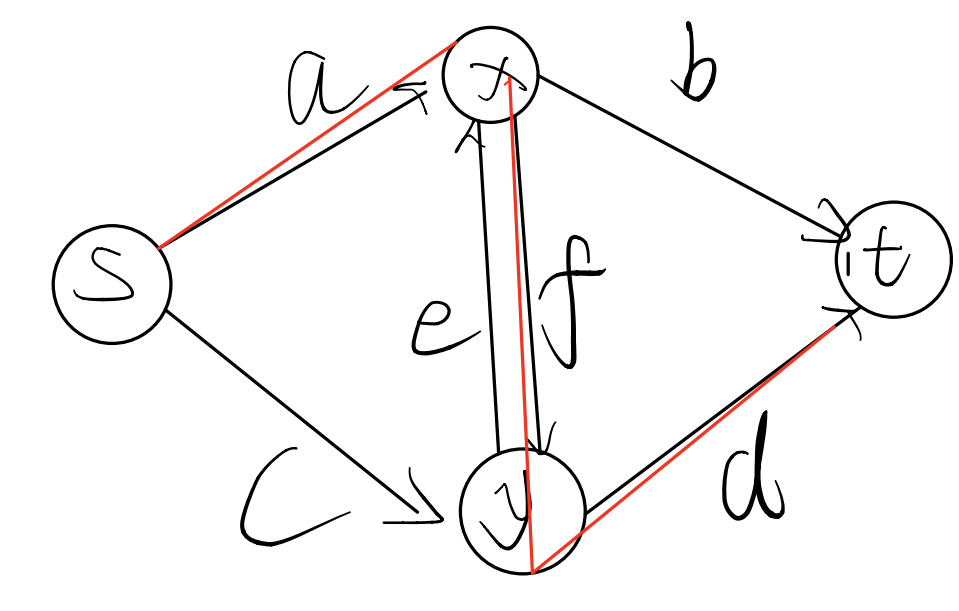
能形成割的形式：

1. a+c:代表都选；
2. b+d:代表都不选；
3. a+e+d：代表只选x
4. c+f+b：代表只选y

接着就定义边权来让上述意义成立，同时也要考虑这个总和的要是哪些量之和。

因为题目有强条件：w，v0，v1，v2均为偶数。所以我们考虑可以把这些数拆成一半

因此连边：

1. 源点到每个 i 连容量为所有约束的v1的一半
2. 每个点 i 到汇点连容量为所有约束的v0的一半+w[i]
3. 所有约束之间连（v0+v1）/2 + v2的容量的边

接着总和就是v0+v1+w[i]之和；

最后答案就是总和-最小割.

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define lson root<<1,l,midd
#define rson root<<1|1,midd+1,r
#define pb push_back
const int inf=0x3f3f3f3f;
const ll INF=(1ll<<40);
const int M=7e4+4;
const int N=2e6+6;
int tot,s,t,n,m;
struct node{
    int u,v,nextt,w;
}e[N];
int head[M],deep[M],cur[M];
void addedge(int u,int v,int w){
    e[tot].v=v;
    e[tot].w=w;
    e[tot].nextt=head[u];
    head[u]=tot++;
    e[tot].v=u;
    e[tot].w=0;
    e[tot].nextt=head[v];
    head[v]=tot++;
}
bool bfs(){
    memset(deep,0,sizeof(deep));
    queue<int>que;
    que.push(s);
    deep[s]=1;
    while(!que.empty()){
        int u=que.front();
        que.pop();
        for(int i=head[u];i!=-1;i=e[i].nextt){
            int v=e[i].v;
            if(e[i].w>0&&deep[v]==0){
                deep[v]=deep[u]+1;
                if(v==t)
                    return true;
                que.push(v);
            }
        }
    }
    return deep[t]==0?false:true;
}
int dfs(int u,int fl){
    if(u==t)
        return fl;
    int x=0,ans=0;
    for(int i=cur[u];i!=-1;i=e[i].nextt){
        int v=e[i].v;
        if(deep[u]+1==deep[v]&&e[i].w>0){
            x=dfs(v,min(fl-ans,e[i].w));
            e[i].w-=x;
            e[i^1].w+=x;
            if(e[i].w)
                cur[u]=i;
            ans+=x;
            if(ans==fl)
                return fl;
        }
    }
    if(ans==0)
        deep[u]=0;
    return ans;
}
int dinic(){
    int ans=0;
    while(bfs()){
        for(int i=0;i<=t;i++)
            cur[i]=head[i];
        ans+=dfs(s,inf);
    }
    return ans;
}
void init(){
    tot=0;
    memset(head,-1,sizeof(head));
}
int w[M],sumv1[M],sumv0[M];
int main(){
    init();
    scanf("%d%d",&n,&m);
    int sum=0;
    for(int i=1;i<=n;i++){
        scanf("%d",&w[i]);
        sum+=w[i];
    }
    while(m--){
        int x,y,v0,v1,v2;
        scanf("%d%d%d%d%d",&x,&y,&v0,&v1,&v2);
        sum+=v0+v1;
        sumv1[x]+=v1/2,sumv1[y]+=v1/2;
        sumv0[x]+=v0/2,sumv0[y]+=v0/2;
        addedge(x,y,(v0+v1)/2+v2);
        addedge(y,x,(v0+v1)/2+v2);
    }
    s=0,t=n+1;
    for(int i=1;i<=n;i++){
        addedge(s,i,sumv1[i]);
        addedge(i,t,sumv0[i]+w[i]);
    }
    printf("%d\n",sum-dinic());
    return 0;
}

 学习自：https://blog.csdn.net/u013534123/article/details/87614758