概率-期望粗学

引用：https://blog.csdn.net/auto_ac/article/details/9907881

很多概率题总逃不开用dp转移。

期望题总是倒着推过来的，概率是正着推的，多做题就会理解其中的原因

有些期望题要用到有关概率或期望的常见公式或思想

遇到dp转移方程(组)中有环的，多半逃不出高斯消元（手动和写代码两种）

这套题中还有道树上的dp转移，还用dfs对方程迭代解方程，真是大开眼界了

当然还有与各种算法结合的题，关键还是要学会分析

当公式或计算时有除法时，特别要注意分母是否为零

概率：

入门题：http://acm.hdu.edu.cn/showproblem.php?pid=3853

题意：一开始在矩阵左上角，每次有三种可能的选择（有对应的概率）向下走、向右走、原地不动，每次都有2的消耗，问到矩阵右下角的期望消耗是多少？

分析：设dp[i][j]表示从位置[i,j]到右下角的期望，那么dp[i][j]=dp[i][j]*(原地不动的概率)+dp[i+1][j]*(向下走的概率）+dp[i][j+1]*(向右走的概率）移项得公式

#include<cstdio>
using namespace std;
const int M=1003;
double p[M][M][5],dp[M][M];
int main(){
    int n,m;
    while(~scanf("%d%d",&n,&m)){
        for(int i=1;i<=n;i++)
            for(int j=1;j<=m;j++)
                scanf("%lf%lf%lf",&p[i][j][1],&p[i][j][2],&p[i][j][3]);
        dp[n][m]=0;
        for(int i=1;i<=n;i++)
            dp[i][m+1]=0;
        for(int i=1;i<=m;i++)
            dp[n+1][i]=0;
        for(int i=n;i>0;i--){
            for(int j=m;j>0;j--){
                if(p[i][j][1]==1||i==n&&j==m)
                    continue;
                dp[i][j]=(dp[i+1][j]*p[i][j][3]+dp[i][j+1]*p[i][j][2]+2)/(1-p[i][j][1]);
            }

        }
        printf("%.3f\n",dp[1][1]);
    }
    return 0;
}

View Code

练习：

题1：http://poj.org/problem?id=3744

题意：在水平面上设置一些类似障碍的东西，然后一个人从位置1开始行动，有p的概率跳一个单位，有1-p的概率跳俩个单位，问这个人跳过全部障碍的概率是多少；

分析：对于这个公式应该一秒就出来了，不过给定的n个障碍物的位置会达到10^8级别，所以我们用矩阵快速幂来解决（类似就菲...数列一样）构造出基矩阵就行

#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
double c[2][2],b[2][2],t[2][2];
int a[100];
double p;
void mul(double x[][2],double y[][2]){///return x=x*y
    for(int i=0;i<2;i++)
        for(int j=0;j<2;j++)
            c[i][j]=0;
    for(int i=0;i<2;i++)
    for(int j=0;j<2;j++){
        for(int k=0;k<2;k++)
            c[i][j]+=x[i][k]*y[k][j];
    }
    for(int i=0;i<2;i++)
        for(int j=0;j<2;j++)
            x[i][j]=c[i][j];
}
void sksm(int n){
    b[0][0]=p,    b[0][1]=1;
    b[1][0]=1.0-p,b[1][1]=0;
    t[0][0]=1,t[0][1]=0;
    t[1][0]=0,t[1][1]=1;
    while(n){
        if(n&1){
            mul(t,b);
        }
        mul(b,b);
        n>>=1;
    }
}
int main(){
    int n;
    while(~scanf("%d%lf",&n,&p)){
        for(int i=0;i<n;i++)
            scanf("%d",&a[i]);
        sort(a,a+n);
        double ans=1.0;
        sksm(a[0]-1);
        ans*=(1-t[0][0]);
        for(int i=1;i<n;i++){
            sksm(a[i]-a[i-1]-1);
            ans*=(1-t[0][0]);
        }
        printf("%.7f\n",ans);
    }
    return 0;
}

View Code

题2：http://poj.org/problem?id=3071

题意：模拟足球比赛淘汰制，给定每个球队战胜别的球队的概率，输出能最后胜出的球队的编号

分析：用dp算出所有队伍每次晋级的dp值依次往上推就行

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>

using namespace std;
typedef long long ll;
const int M=266;
double a[M][M],dp[M],c[M];
int main(){
    int t;
    while(~scanf("%d",&t)){
        if(t==-1)
            break;
        int n=1;
        for(int i=1;i<=t;i++)
            n<<=1;
        //cout<<n<<endl;
        for(int i=1;i<=n;i++){
            dp[i]=1.0;
            for(int j=1;j<=n;j++)
                scanf("%lf",&a[i][j]);
        }
        int nowlen=1;
        for(int i=1;i<=t;i++){
            for(int j=1;j<=n;j++)
                c[j]=dp[j],dp[j]=0;
            nowlen<<=1;
            for(int j=1;j<=n;j+=nowlen){
                
                int l=j,r=j+nowlen-1;
                int midd=(l+r)>>1;
                for(int k=l;k<=midd;k++){
                    for(int p=midd+1;p<=r;p++)
                        dp[k]+=c[k]*a[k][p]*c[p];
                }
                for(int k=midd+1;k<=r;k++){
                    for(int p=l;p<=midd;p++)
                        dp[k]+=c[k]*a[k][p]*c[p];
                }
            }
        }    
        double maxx=0;
        int ansi=1;
        for(int i=1;i<=n;i++){
            if(maxx-dp[i]<0){
                maxx=dp[i];
                ansi=i;
            }
        //    printf("%.7f\n",dp[i]);
        }
        printf("%d\n",ansi);
    }
    return 0;
}

View Code

题3：http://codeforces.com/problemset/problem/148/D

题意：有w只白鼠，b只黑鼠，问先手抓到第一次白鼠的概率，其中后手抓完后在所有老鼠中会随机地跑掉一只

分析：记忆化搜索

#include<bits/stdc++.h>
using namespace std;
const int M=1e3+3;
int vis[M][M];
double dp[M][M];
double dfs(int noww,int nowb){
    if(noww<=0)
        return 0;
    if(nowb<=0)
        return 1;
    if(vis[noww][nowb]==1)
        return dp[noww][nowb];
    vis[noww][nowb]=1;
    double &res=dp[noww][nowb];
    res=noww*1.0/(noww+nowb);///这次取到白色
    if(nowb>=2){
        ///失败俩次来捉黑鼠
        double x=nowb*1.0/(noww+nowb);
        nowb--;
        x*=nowb*1.0/(noww+nowb);
        nowb--;
        ///             白鼠溜了                            黑鼠溜了
        res+=x*(noww*1.0/(noww+nowb)*dfs(noww-1,nowb))+x*(nowb*1.0/(nowb+noww)*dfs(noww,nowb-1));
    }
    return res;
}
int main(){
    double n,m;
    scanf("%lf%lf",&n,&m);
    printf("%.9f\n",dfs(n,m));
    return 0;
}

View Code

期望：

题1：https://ac.nowcoder.com/acm/contest/697/A

分析：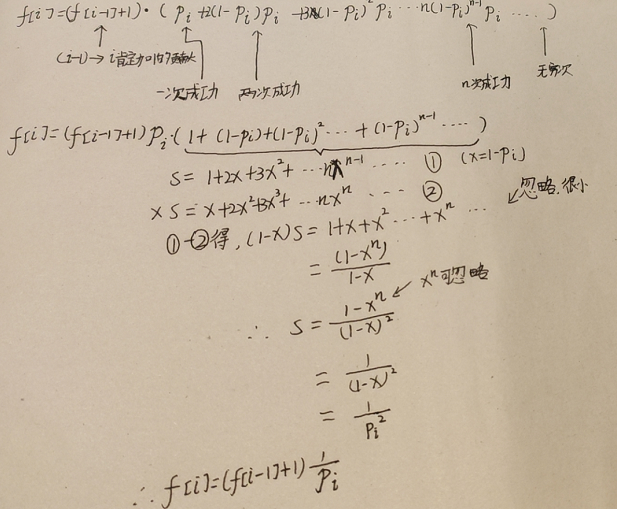

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod=1000000007;
const int M=2e5+5;
ll dp[M];
ll ksm(ll a,ll b){
    ll t=1;
    while(b){
        if(b&1)
            t=t*a%mod;
        a=a*a%mod;
        b>>=1;
    }
    return t;
}
int main(){
    int n;
    scanf("%d",&n);
    for(int i=1;i<=n;i++){
        ll x,y;
        scanf("%I64d%I64d",&x,&y);
        dp[i]=(dp[i-1]+1)*y%mod*ksm(x,mod-2)%mod;
    }
    printf("%I64d",dp[n]);
}

View Code

posted @ 2019-12-08 15:23 starve_to_death 阅读(276) 评论(0) 编辑收藏举报

刷新页面返回顶部

starve_to_death

概率-期望粗学

公告