机器学习-朴素贝叶斯
标签: 机器学习
1. 贝叶斯公式是机器学习中常用的计算方法,例如,甲射中靶标的概率是0.4,乙射中靶标的概率是0.8,现在有个人中靶了,问问是甲射中的概率。这非常好计算,P=0.4/(0.8+0.4)=0.33,这是贝叶斯公式的基本应用,具体的贝叶斯公式如下:
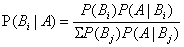
2.《机器学习实战》中的贝叶斯实现:
略有修改,已经在本地电脑通过测试,可以运行
import numpy as np
#-_-_-_-_-_-
dataset=[['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],
['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
['stop', 'posting', 'stupid', 'worthless', 'garbage'],
['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]
classVec = [0,1,0,1,0,1]
#将出现的所有单词放在一个列表中,再将列表转为集合,(调用的时候再转化为列表)
def createVocabList(dataSet0):
vocalist=[]
for i in dataSet0:
for d in i :
vocalist.append(d)
return set(vocalist)
#将数据转为向量,类似于one_hot编码
def setOfWords2Vec(vocabList, inputSet):
temp_vector=np.zeros((len(vocabList)))
for i in inputSet:
if i in vocabList:
temp_vector[vocabList.index(i)]=1
return temp_vector
##核心部分,训练算法
#输入 trainMatrix [[0,1 0.....],[0.1,1,1 0......],....]
# 输入trainCategory,标签[0,1,0,1,0,1]
# classifyNB函数会用到贝叶斯公式p(c|w)=p(c)p(w|c)/p(w)
# p(c)比较容易求
#
def trainNB0(trainMatrix,trainCategory):
numTrainDocs = len(trainMatrix)
numWords = len(trainMatrix[0])
pAbusive = sum(trainCategory)/float(numTrainDocs) #p(c)
#这里之所以不初始为0,是因为p(w|c),可以看成p(w0,w1,w2...|c)
#如果假设特征之间相互独立,则写成
#p(w0|ci)p(w1|ci)p(w2|ci)...p(wN|ci)
#所以为了防止其中一个为0,导致整体概率为0,须将数值初始化为1,分母初始为2
p0Num = np.ones(numWords); p1Num = np.ones(numWords) #change to ones()
p0Denom = 2.0; p1Denom = 2.0 #change to 2.0
for i in range(numTrainDocs):
if trainCategory[i] == 1:
p1Num += trainMatrix[i]
p1Denom += sum(trainMatrix[i])
else:
p0Num += trainMatrix[i]
p0Denom += sum(trainMatrix[i])
#Python在很多小数相乘的时候,会产生下溢,因为精度不够,所以改成log
p1Vect = np.log(p1Num/p1Denom) #change to log()
p0Vect = np.log(p0Num/p0Denom) #change to log()
return p0Vect,p1Vect,pAbusive
#核心算法,利用贝叶斯进行分类
def classifyNB(vec2Classify, p0Vec, p1Vec, pClass1):
# 因为在训练的时候转成了log,所以乘法变加法log(a*b)=log(a)+log(b)
p1 = sum(vec2Classify * p1Vec) + np.log(pClass1) #分母一样,故把分母省略了
p0 = sum(vec2Classify * p0Vec) + np.log(1.0 - pClass1)
if p1 > p0:
return 1
else:
return 0
if __name__=='__main__':
temp_set=createVocabList(dataset)
word_list=list(temp_set)
trainmatrix=[]
for item in dataset:
temp_vector=setOfWords2Vec(word_list,item)
trainmatrix.append(temp_vector)
p0Vect, p1Vect, pAbusive=trainNB0(trainmatrix,classVec)
#这是我测试用的,如果输出为0,就是正确的
#这个test向量对应的是我自己设置的词列表['cute','love']
test=np.zeros(len(word_list))
test[0]=1
test[1]=1
b=classifyNB(test,p0Vect,p1Vect,pAbusive)
print(b)
#输出为0,符合预期
3. sklearn中的贝叶斯实现:
查看了一下sklearn源代码,GaussianNB主要部分如下所示:
def _joint_log_likelihood(self, X):
check_is_fitted(self, "classes_")
X = check_array(X)
joint_log_likelihood = []
for i in range(np.size(self.classes_)):
#####这一部分和上边的classifyNB函数代码大同小异--------
jointi = np.log(self.class_prior_[i])
n_ij = - 0.5 * np.sum(np.log(2. * np.pi * self.sigma_[i, :]))
n_ij -= 0.5 * np.sum(((X - self.theta_[i, :]) ** 2) /
(self.sigma_[i, :]), 1)
joint_log_likelihood.append(jointi + n_ij)
#####-------------------------------------------------
joint_log_likelihood = np.array(joint_log_likelihood).T
return joint_log_likelihood
上述的源代码只不过是令公式中的:
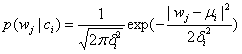
实际应用也非常简单,这个分类一般应用于连续的,符合正态分布的数据上,除此之外,还有一个MultinomialNB,这个一般应用于离散的数据上.这个贝叶斯分类的对应的公式是:
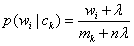
他包含三个参数
alpha:即为上面的常数λ,默认为1,设置的时候稍大于1或者稍小于1
fit_prior:是否考虑先验概率
class_prior:即贝叶斯公式中的P(C),在fit_prior为true的情况下,如果不填这个参数,他会从样本中计算.


 浙公网安备 33010602011771号
浙公网安备 33010602011771号