csps模拟测试61
对于考试状态比较满意,正确选择难度梯度进行思考。
主要是题水。
T1:淼淼淼模拟
爆写200行

1 #include<iostream> 2 #include<cstdio> 3 #include<vector> 4 #include<cstring> 5 #include<algorithm> 6 using namespace std; 7 const int N=2010; 8 int maxi,k,v[N][N]; 9 char a[N]; 10 void add(int x,int y) 11 { 12 v[x+1000][y+1000]++; 13 maxi=max(maxi,v[x+1000][y+1000]); 14 } 15 vector<int>vx,vy; 16 struct node 17 { 18 int x,y,a,b,op; 19 void rotate(char d,int jud) 20 { 21 if(d=='N'&&op==0) 22 { 23 op=1;y++; 24 b+=k; 25 } 26 else if(d=='N'&&op==1) 27 { 28 if(b-y==k) 29 { 30 op=0;b++; 31 y+=k; 32 } 33 else 34 { 35 op=1;b++; 36 y++; 37 } 38 } 39 else if(d=='S'&&op==0) 40 { 41 op=1;y-=k; 42 b--; 43 } 44 else if(d=='S'&&op==1) 45 { 46 if(b-y==k) 47 { 48 op=0;y--; 49 b-=k; 50 } 51 else 52 { 53 op=1;y--; 54 b--; 55 } 56 } 57 else if(d=='E'&&op==0) 58 { 59 op=1;x++; 60 a+=k; 61 } 62 else if(d=='E'&&op==1) 63 { 64 if(b-y==k) 65 { 66 op=1;x++; 67 a++; 68 } 69 else 70 { 71 op=0;x+=k; 72 a++; 73 } 74 } 75 else if(d=='W'&&op==0) 76 { 77 op=1;x-=k; 78 a--; 79 } 80 else if(d=='W'&&op==1) 81 { 82 if(b-y==k) 83 { 84 op=1;x--; 85 a--; 86 } 87 else 88 { 89 op=0;x--; 90 a-=k; 91 } 92 } 93 for(int i=x;i<a;i++) 94 for(int j=y;j<b;j++) 95 { 96 add(i,j); 97 if(jud==1) vx.push_back(i),vy.push_back(j); 98 } 99 } 100 }; 101 inline int rd() 102 { 103 int s=0,w=1; 104 char cc=getchar(); 105 for(;cc<'0'||cc>'9';cc=getchar()) if(cc=='-') w=-1; 106 for(;cc>='0'&&cc<='9';cc=getchar()) s=(s<<3)+(s<<1)+cc-'0'; 107 return s*w; 108 } 109 void work() 110 { 111 k=rd(); 112 scanf("%s",a+1);int n=strlen(a+1); 113 memset(v,0,sizeof(v)); 114 maxi=0;vx.clear();vy.clear(); 115 node s=(node){0,0,1,1,0}; 116 add(0,0); 117 for(int i=1;i<n;i++)s.rotate(a[i],0); 118 s.rotate(a[n],1); 119 sort(vx.begin(),vx.end()); 120 sort(vy.begin(),vy.end()); 121 for(int i=0;i<vx.size();i++) printf("%d ",vx[i]);puts(""); 122 for(int i=0;i<vy.size();i++) printf("%d ",vy[i]); 123 printf("\n%d\n",maxi); 124 } 125 int main() 126 { 127 int T=rd(); 128 while(T--){work();} 129 } 130 /* 131 g++ -std=c++11 1.cpp -o 1 132 ./1 133 3 134 2 135 ENEESESSESWWWN 136 5 137 WNSEWNSEWNSEWWSEN 138 3 139 NNEEESESWWNWWWWWSSEEEEENNE 140 */
T3:维护线段树,题解是维护hash,很好的思路,但是一般hash是正解的题不多。
我的思路是维护懒标记。首先如果要转移对,一定要吧懒标记合并好,一般我线段树打错的题,都是懒标记直接赋值啥的。
之前有道离散化+线段树的题(就前几次考试),值得一提,
那次有一个懒标记,我的思路是不合并,每次遇到就下传,好像就不会有合并。
但是有bug,在于我如果这样的操作在下穿的时候应该吧儿子的东西也下传给孙子。
然后就失去了懒标记的意义。
所以 懒标记一定要想好合并。
这个题我就知道很麻烦,所以我打了对拍,拍出了4处错误,调了一个小时。
首先这个题的懒标记应该表示一个区间,表示从上次下传到现在,连续的赋值操作从谁到谁,所以懒标记要有两个。
如果赋值操作不是连续的那么这整个区间都不可以,直接赋值-2。
然后赋值-1代表他可以承接任何赋值。也就是我懒标记下传后的空状态。
如果没有这个空状态,可能先给自己赋34,再给儿子赋12,就不能传对了。
总之要搞清逻辑关系,只要这个区间的赋值操作是连续的,他就有可能更新儿子,所以我应该存下,如果这个已经是-2了,那就一定不行。
最终底层节点状态赋值0,代表承接1的赋值,然后所有其他节点赋值-1,可以承接所有。
懒标记传递看自己的起始状态,能不能接上儿子的终止状态,如果可以儿子终止状态增加。
然后最后把懒标记全都下传。

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #define int long long 5 const int N=130,cu=1e9; 6 long long f[N],mod,phi; 7 char s[N]; 8 using namespace std; 9 struct hint 10 { 11 int bin[13]; 12 void clear(){memset(bin,0,sizeof(bin));} 13 int &operator [](int i){return bin[i];} 14 void rd() 15 { 16 scanf("%s",s);bin[0]=(strlen(s)+9)/9; 17 int tmp=strlen(s)-1; 18 for(int i=1;i<=bin[0];i++) 19 { 20 int tu=1; 21 for(int j=tmp;j>tmp-9&&j>=0;j--) 22 { 23 bin[i]=bin[i]+(s[j]-'0')*tu; 24 tu*=10; 25 } 26 tmp-=9; 27 } 28 //cout<<strlen(s)<<endl; 29 while(!bin[bin[0]]&&bin[0]>1) bin[0]--; 30 } 31 int operator %(int p) 32 { 33 hint c;c.clear(); 34 long long i,x=0; 35 for(i=bin[0];i;i--) 36 { 37 c[i]=(x*cu+bin[i])/p; 38 x=(x*cu+bin[i])%p; 39 } 40 return x; 41 } 42 hint operator /(int p) 43 { 44 hint c;c.clear(); 45 int i,x=0; 46 for(i=bin[0];i;i--) 47 { 48 c[i]=(x*cu+bin[i])/p; 49 x=(x*cu+bin[i])%p; 50 } 51 c[0]=bin[0]; 52 while (c[c[0]]==0&&c[0]>1)c[0]--; 53 return c; 54 } 55 hint operator /=(int p) {return *this=*this/p;} 56 }; 57 inline long long rd() 58 { 59 long long s=0,w=1; 60 char cc=getchar(); 61 for(;cc<'0'||cc>'9';cc=getchar()) if(cc=='-') w=-1; 62 for(;cc>='0'&&cc<='9';cc=getchar()) s=(s<<3)+(s<<1)+cc-'0'; 63 return s*w; 64 } 65 long long qpow(long long a,hint d) 66 { 67 long long ans=1,k=d%phi; 68 for(a%=mod,k%=phi;k>0;k>>=1,a=1ll*a*a%mod) if(k&1) ans=1ll*ans*a%mod; 69 return ans; 70 } 71 long long qpow(long long a,long long k) 72 { 73 long long ans=1; 74 for(a%=mod,k%=phi;k>0;k>>=1,a=1ll*a*a%mod) if(k&1) ans=1ll*ans*a%mod; 75 return ans; 76 } 77 void work_1(long long n,long long k) 78 { 79 int ans2=0,ans5=0,ans=1,mod; 80 if(k==1) mod=10; 81 if(k==2) mod=100; 82 if(k==3) mod=1000; 83 for(int i=2;n/i>0;i<<=1) 84 ans2+=n/i; 85 for(int i=5;n/i>0;i*=5) 86 ans5+=n/i; 87 ans2=min(ans2,ans5); 88 ans5=min(ans2,ans5); 89 for(register int i=1;i<=n;i++) 90 { 91 register int tmp=i; 92 while(tmp%2==0&&ans2>0) tmp/=2,ans2--; 93 while(tmp%5==0&&ans5>0) tmp/=5,ans5--; 94 ans=1ll*ans*tmp%mod; 95 } 96 if(k==1)printf("%01lld\n",ans); 97 if(k==2)printf("%02lld\n",ans); 98 if(k==3)printf("%03lld\n",ans); 99 } 100 int work_2(int n) 101 { 102 int ans=1; 103 for(int i=1;i<=n;i++) 104 { 105 int tmp=i; 106 while(tmp%5==0) tmp/=5; 107 ans=ans*tmp%mod; 108 } 109 //cout<<ans<<endl; 110 return ans; 111 } 112 int solve(hint n) 113 { 114 if(n[0]==1&&n[1]<=100) return work_2(n[1]); 115 return 1ll*solve(n/5)*qpow(f[mod],n/mod)%mod*f[n%mod]%mod; 116 } 117 signed main() 118 { 119 //freopen("ex_num2.in","r",stdin); 120 int T=rd(); 121 while(T--) 122 { 123 hint n;long long fp_5=0;n.clear(); 124 n.rd(); 125 int k=rd(),ct; 126 f[0]=1; 127 if(n[0]==1&&n[1]<=1000) 128 { 129 work_1(n[1],k); 130 continue; 131 } 132 if(k==1) mod=5,ct=2,phi=4; 133 if(k==2) mod=25,ct=4,phi=20; 134 if(k==3) mod=125,ct=8,phi=100; 135 hint tmp=n; 136 while("wwn") 137 { 138 if(tmp[0]==1&&tmp[1]==0) break; 139 140 tmp/=5; 141 142 fp_5=(fp_5+tmp%phi)%phi; 143 //cout<<1<<endl; 144 } 145 for(int i=1;i<=mod;i++) 146 { 147 if(i%5!=0)f[i]=1ll*f[i-1]*i%mod; 148 else f[i]=f[i-1]; 149 } 150 int ans=solve(n); 151 ans=1ll*ans*qpow(qpow(2,fp_5),phi-1)%mod; 152 while(ans%ct) ans+=mod; 153 if(k==1)printf("%01lld\n",ans); 154 if(k==2)printf("%02lld\n",ans); 155 if(k==3)printf("%03lld\n",ans); 156 } 157 } 158 /* 159 g++ 1.cpp -o 1 160 ./1 161 1 162 1234567891234567845645132132465462132165454654651321321651321316065160506412561561651654657897453964 3 163 */
T2:数学题,题解很帅。
设我要从$n!$中去掉所有$10$的值为$solve(10,n)$
那么通过一些推导可以知道,$n!$中2的蜜次比5的蜜次一定多,然后我就可以,得到$solve(5,n)*2^fp_5$ fp表示含5的蜜次。
然后通过另外一些推导。

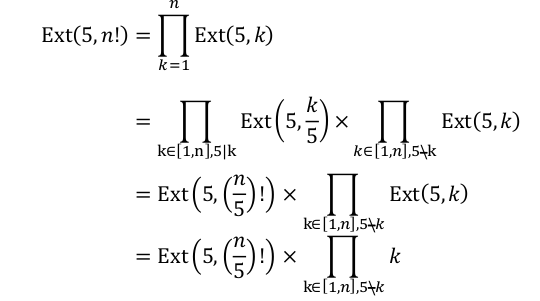
问题成功的转化为子问题,并且是除以5,复杂度是$log_5n$级别。
最终如果n很小一些性质不符合以及递归的边界,直接跑暴力即可。

#include<iostream> #include<cstdio> #include<cstring> #define int long long const int N=130,cu=1e9; long long f[N],mod,phi; char s[N]; using namespace std; struct hint { int bin[13]; void clear(){memset(bin,0,sizeof(bin));} int &operator [](int i){return bin[i];} void rd() { scanf("%s",s);bin[0]=(strlen(s)+9)/9; int tmp=strlen(s)-1; for(int i=1;i<=bin[0];i++) { int tu=1; for(int j=tmp;j>tmp-9&&j>=0;j--) { bin[i]=bin[i]+(s[j]-'0')*tu; tu*=10; } tmp-=9; } //cout<<strlen(s)<<endl; while(!bin[bin[0]]&&bin[0]>1) bin[0]--; } int operator %(int p) { hint c;c.clear(); long long i,x=0; for(i=bin[0];i;i--) { c[i]=(x*cu+bin[i])/p; x=(x*cu+bin[i])%p; } return x; } hint operator /(int p) { hint c;c.clear(); int i,x=0; for(i=bin[0];i;i--) { c[i]=(x*cu+bin[i])/p; x=(x*cu+bin[i])%p; } c[0]=bin[0]; while (c[c[0]]==0&&c[0]>1)c[0]--; return c; } hint operator /=(int p) {return *this=*this/p;} }; inline long long rd() { long long s=0,w=1; char cc=getchar(); for(;cc<'0'||cc>'9';cc=getchar()) if(cc=='-') w=-1; for(;cc>='0'&&cc<='9';cc=getchar()) s=(s<<3)+(s<<1)+cc-'0'; return s*w; } long long qpow(long long a,hint d) { long long ans=1,k=d%phi; for(a%=mod,k%=phi;k>0;k>>=1,a=1ll*a*a%mod) if(k&1) ans=1ll*ans*a%mod; return ans; } long long qpow(long long a,long long k) { long long ans=1; for(a%=mod,k%=phi;k>0;k>>=1,a=1ll*a*a%mod) if(k&1) ans=1ll*ans*a%mod; return ans; } void work_1(long long n,long long k) { int ans2=0,ans5=0,ans=1,mod; if(k==1) mod=10; if(k==2) mod=100; if(k==3) mod=1000; for(int i=2;n/i>0;i<<=1) ans2+=n/i; for(int i=5;n/i>0;i*=5) ans5+=n/i; ans2=min(ans2,ans5); ans5=min(ans2,ans5); for(register int i=1;i<=n;i++) { register int tmp=i; while(tmp%2==0&&ans2>0) tmp/=2,ans2--; while(tmp%5==0&&ans5>0) tmp/=5,ans5--; ans=1ll*ans*tmp%mod; } if(k==1)printf("%01lld\n",ans); if(k==2)printf("%02lld\n",ans); if(k==3)printf("%03lld\n",ans); } int work_2(int n) { int ans=1; for(int i=1;i<=n;i++) { int tmp=i; while(tmp%5==0) tmp/=5; ans=ans*tmp%mod; } //cout<<ans<<endl; return ans; } int solve(hint n) { if(n[0]==1&&n[1]<=100) return work_2(n[1]); return 1ll*solve(n/5)*qpow(f[mod],n/mod)%mod*f[n%mod]%mod; } signed main() { //freopen("ex_num2.in","r",stdin); int T=rd(); while(T--) { hint n;long long fp_5=0;n.clear(); n.rd(); int k=rd(),ct; f[0]=1; if(n[0]==1&&n[1]<=1000) { work_1(n[1],k); continue; } if(k==1) mod=5,ct=2,phi=4; if(k==2) mod=25,ct=4,phi=20; if(k==3) mod=125,ct=8,phi=100; hint tmp=n; while("wwn") { if(tmp[0]==1&&tmp[1]==0) break; tmp/=5; fp_5=(fp_5+tmp%phi)%phi; //cout<<1<<endl; } for(int i=1;i<=mod;i++) { if(i%5!=0)f[i]=1ll*f[i-1]*i%mod; else f[i]=f[i-1]; } int ans=solve(n); ans=1ll*ans*qpow(qpow(2,fp_5),phi-1)%mod; while(ans%ct) ans+=mod; if(k==1)printf("%01lld\n",ans); if(k==2)printf("%02lld\n",ans); if(k==3)printf("%03lld\n",ans); } } /* g++ 1.cpp -o 1 ./1 1 1234567891234567845645132132465462132165454654651321321651321316065160506412561561651654657897453964 3 */


 浙公网安备 33010602011771号
浙公网安备 33010602011771号