约瑟夫类问题研究

　　今天考试T2挂了（众人皆A我独挂），于是写一个关于约瑟夫类问题的心得。

　　约瑟夫问题：n个人（编号1~n)，从1开始报数，报到m的退出，剩下的人继续从1开始报数。按顺序输出列者编号

　　

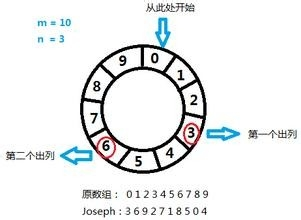
　　参图示。

　　模拟是$O(nm)$的，然后我就死了。n,m给到1e8。

　　做这么多年题大体上发现，如果你的解法超时，多半是因为处理了许多没有用的信息。

　　那么看一看模拟处理出了那些没用信息：他可以知道每一轮谁死了。但是题目不需要知道这些，总之一驼人之前死掉了就可以了。

　　那么我们可以这么想，要求：在不能知道每一轮是谁死了的情况下求出胜者。

　　如果这个问题解决那么它应该是符合时间限制的。

　　切换思路：我们考虑的时候，不把它考虑成2死了然后就没有2了，而是考虑成2死了就把2的编号重新赋给一个人。这是解题的关键。

　　然后就紧紧抓住这个进行计算，首先我在最后一轮的胜者必定是0，因为只有一个人，然后我就关注这个人的编号是怎么变化的就行了。

　　然后就可以推回去，每次根据标的号和人一层一层退回去。

　　具体来说：剩i个人，第n+1-i个人：那么一定是从0开始找m个人，设为k，那么k=(m%i)-1号会死。

　　即：0,1,2,……,k-1,k,……,n-i

　　然后我们把k干掉，重新编号。

　　k+1,……,n-i,0,1,2,……k-1

　　0,1,……n-i-k,k,k+1,……n-i-1

　　重新标号的规则就是id'=(id-k)%i

　　然后我们就可以通过标号的一次次变化来递推了。

　　f[i]=(f[i-1]+m)%i

#include<cstdio>
using namespace std;
int f[100000020],n,m;
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=2;i<=n;i++)f[i]=(f[i-1]+m)%i;
    printf("%d\n",f[n]+1);
}