20200722题解
下面是我的比赛总结
题目分析:
我们可以发现这几个性质:
- 对于一个整数,上取整==下取整
这个不需要解释
- 对于一个小数,它的上取整-下取整==1
这个不需要解释
\(\text{(example)}\) \(ceil(2.5)-floor(2.5)=3-2=1\)
- 我们要选择相同数目个上取整和下取整
那么我们由性质2可以得到:
- 如果上取整数目大于了应该的一半
那么我们可以减去多了的数目,因为2的性质,所以将任意一个小数从上取整变成下取整都为\(-1\),所以直接减,不需要知道是哪个数。
- 小于了的话(接上文)
因为我们还有整数,所以可以直接忽略。
然后我们相当于做好了初始化的操作,现在只需要讨论最优解。
现在拟图如下:
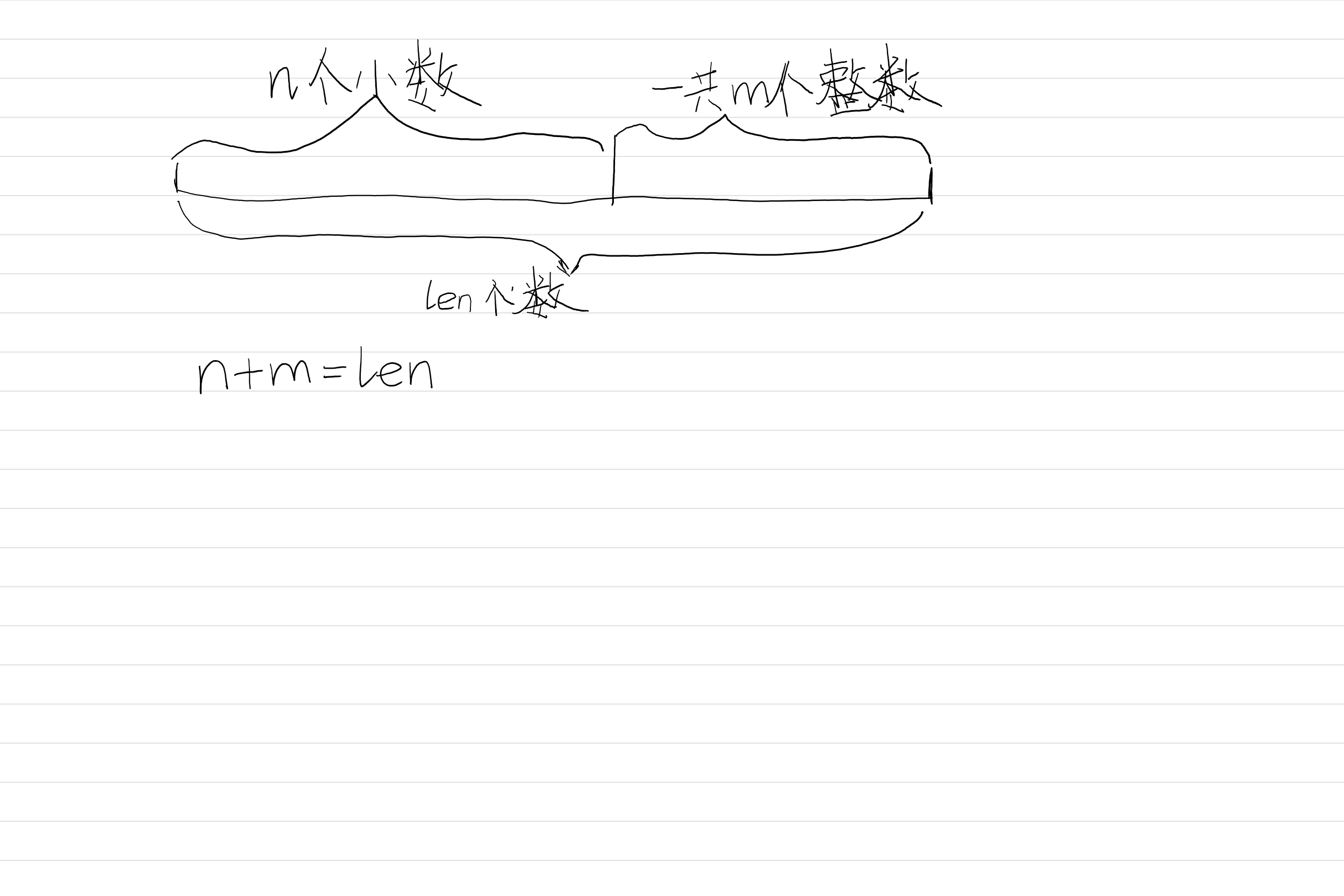
我们已经假设好了东西,现在我们又分类如下
前提:我们的分类是基于调整数列的上取整与下取整,我们必须基于1的性质来进行调整。
- 如果\(n\leq m\)
这时候我们可以随便把上取整的变成下取整
- else
那么我们进行如下讨论:
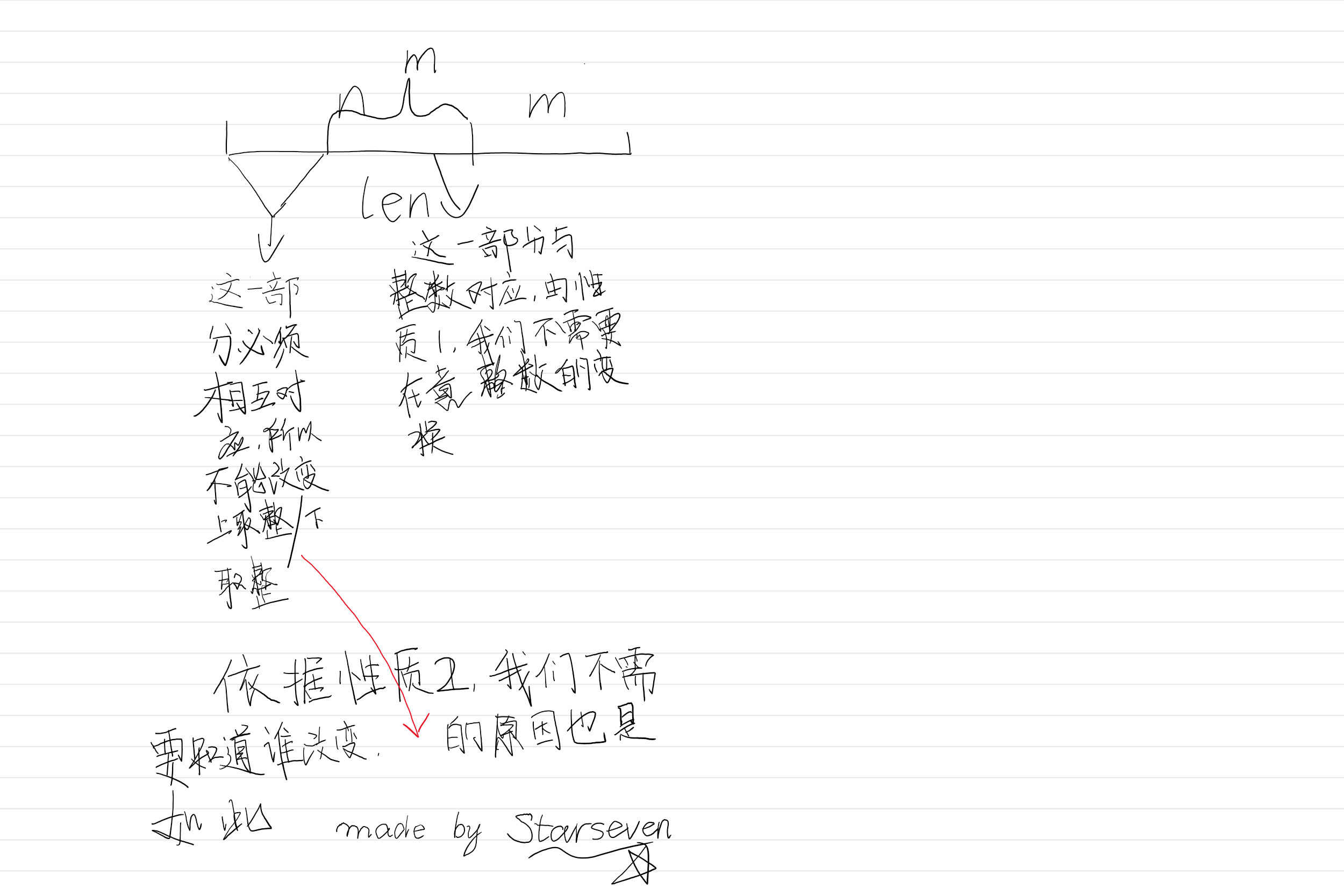
之后代码还要注意一些细节,比如我们初始化是全部上取整,我们就不能再进行上取整对最优化的调整。
代码如下:
#include<cstdio>
#include<cmath>
#include<iostream>
#define ri register int
#define Starseven main
using namespace std;
const int N=5e5+20;
int m,q;
double a[N];
int cei[N],flo[N];
int add[N];
double all[N];
int Starseven(void){
scanf("%d%d",&m,&q);
for(ri i=1;i<=m;i++) scanf("%lf",&a[i]);
for(ri i=1;i<=m;i++){
cei[i]=ceil(a[i]);
flo[i]=floor(a[i]);
if(cei[i]==flo[i]) add[i]++;
all[i]+=(double)cei[i]-a[i];
}
for(ri i=1;i<=m;i++) all[i]+=all[i-1],add[i]+=add[i-1];
// for(ri i=1;i<=m;i++){
// cout<<all[i]<<" "<<add[i]<<endl;
// }
while(q--){
int l,r;
scanf("%d%d",&l,&r);
int numz=add[r]-add[l-1],have=r-l+1;
double gg=all[r]-all[l-1];
// cout<<numz<<" "<<have<<" "<<gg<<endl;
if(numz*2>=have){
int numd=have-numz;
if(gg-numd>0) printf("%.3lf\n",gg-numd);
else {
double ans=ceil(gg)-gg;
double ans2=abs(1-ans);
if(ans>ans2) printf("%.3lf\n",ans2);
else printf("%.3lf\n",ans);
}
}
else{
gg-=(double)((have-numz*2)/2);
int judge=0;
int ce=ceil(gg),fl=floor(gg);
if(gg<0){
printf("%.3lf\n",-gg);
}
else{
if(fl<=numz){
double ans=abs(gg-fl);
if(fl==numz) printf("%.3lf\n",ans);
else{
double judge=abs(1-ans);
if(ans>judge) printf("%.3lf\n",judge);
else printf("%.3lf\n",ans);
}
}
else printf("%.3lf\n",abs(gg-numz));
}
}
}
return 0;
}
/*
6 1
0.000 0.500 0.750 1.000 2.000 3.000
1 6
6 2
0.250 0.250 0.250 0.250 0.250 0.250
1 6
2 5
*/
可是我的代码不够精简,于是这份代码应运而生:
#include<bits/stdc++.h>
using namespace std;
const int N = 5e5 + 5;
int m, q, cnt[N];
double a[N], sum[N], up[N];
int main() {
scanf("%d%d", &m, &q);
for(int i = 1; i <= m; i++) {
scanf("%lf", &a[i]);
sum[i] = sum[i - 1] + a[i], cnt[i] = cnt[i - 1] + (floor(a[i]) != ceil(a[i]));
up[i] = up[i - 1] + ceil(a[i]);
}
while(q--) {
int l, r;
scanf("%d%d", &l, &r);
int n = (r - l + 1) / 2;
double ans = up[r] - up[l - 1], ori = sum[r] - sum[l - 1];
int c = cnt[r] - cnt[l - 1];
if(ans - min(c, n) > ori) ans -= min(c, n);
else {
int maxn = min(c, min(n, (int)(ans - ori + 0.5 - 1e-8))), lst = n - maxn;
ans -= maxn;
if(2 * n - c < lst) ans -= lst - (2 * n - c);
}
printf("%.3lf\n", fabs(ans - ori));
}
return 0;
}
/*
6 1
0.000 0.500 0.750 1.000 2.000 3.000
1 6
*/
嫖的。
这道题真的很妙,可谓基础dfs的好题
我们作以下分析:
- 对于一个点,它到\(a[i],b[i]\)两点的距离到底等于多少?
我们可以看下图所示:
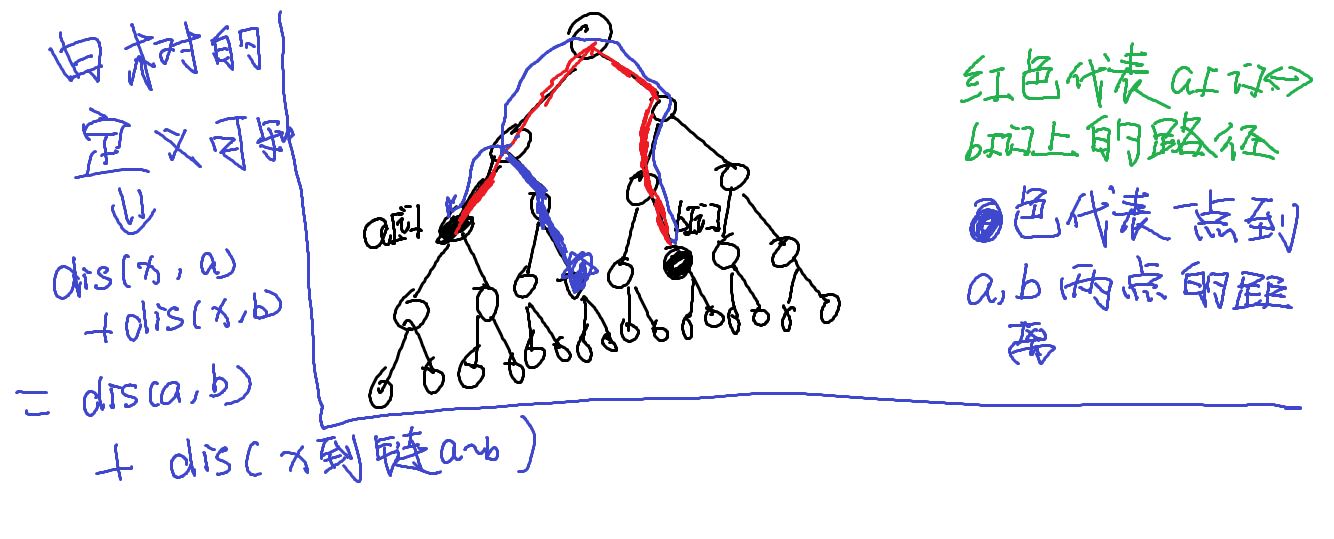
所以我们就可以把点与点的距离转化到点与链的距离(为什么要这样做呢?)
在以上的操作后,我们可以以\(1\)为根搜索(dfs),然后我们就可以得到每个点的深度
注意,有一个OI小常识
当点与点的距离相同,也就是都为一&\(i\)时,我们可以直接将点距变成深度差(前提是点为根)。
在dfs后,我们就得到了第一棵搜索树。
然后我们进行一下操作:
for(ri i=1;i<=m;i++){
cin>>a[i]>>b[i]>>d[i];
if(max(0,dep[a[i]][0]+dep[b[i]][0]-d[i])>maxn) maxn=max(0,dep[a[i]][0]+dep[b[i]][0]-d[i]),maxp=i;
}
这里的\(if\)语句有什么作用呢?
\(dep[a[i]][0]+dep[b[i]][0]-d[i]\) 代表了什么?
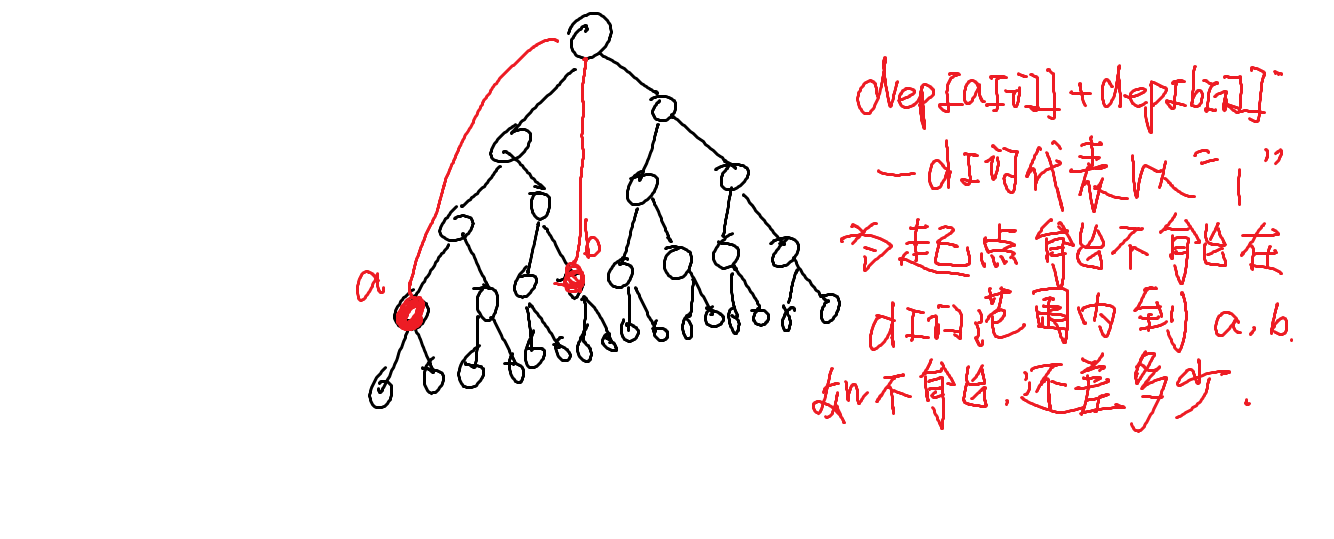
而我们找到最大的不能达到的点的含义是什么呢?
因为在这条\(a[maxp],b[maxp]\)中,起点"1"最不能到达,所以我们肯定在选择点时要以\(maxp\)作为最先考虑点。
所以我们进行第二次和第三次搜索,分别将\(a[maxp],b[maxp]\)作为起点。
Dfs(a[maxp],0,1);Dfs(b[maxp],0,2);
for(ri i=1;i<=n;i++)
if(dep[i][1]+dep[i][2]<=d[maxp]&&(!lit||dep[lit][0]>dep[i][0])) lit=i;
这个时候我们由之前的OI小常识可知,\(dep[i][1]+dep[i][2]<=d[maxp]\)代表的是这个点满足到链的距离\(\leq d[maxp]\)
而我们为什么要\((!lit||dep[lit][0]>dep[i][0])) lit=i;\)呢?
分类讨论:
每一个分类讨论中的树都是第一次dfs形成的树
- 当两个链在同一子树内
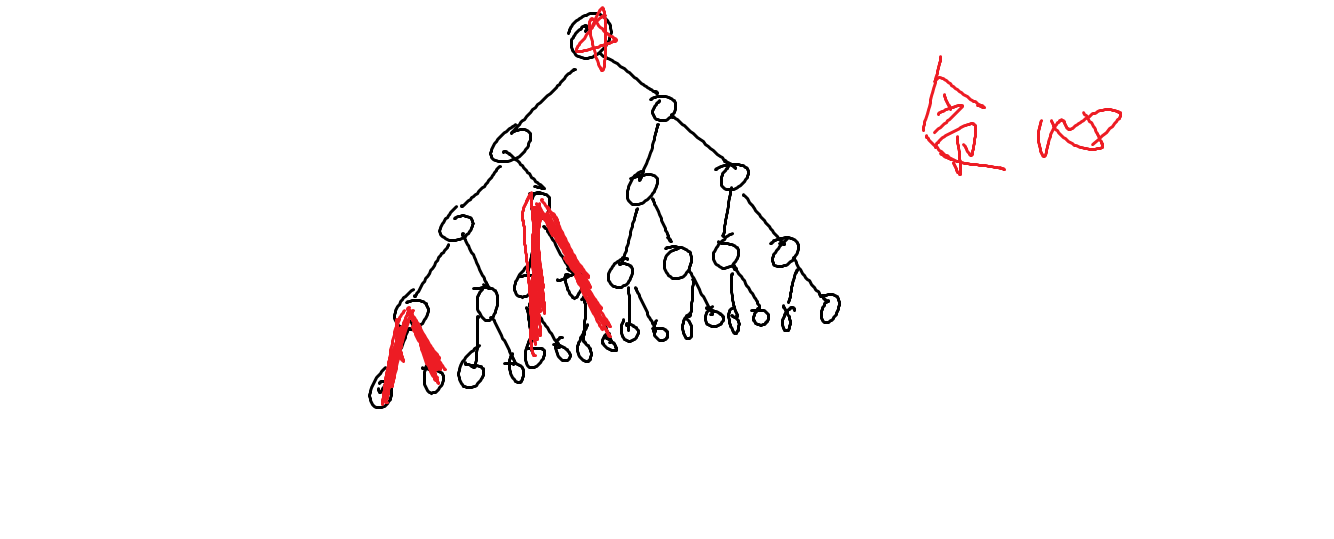
因为我们之前判断了
if(max(0,dep[a[i]][0]+dep[b[i]][0]-d[i])>maxn) maxn=max(0,dep[a[i]][0]+dep[b[i]][0]-d[i]),maxp=i;
所以在同一子树内一定可以满足。
- 当两个链在不同子树内:
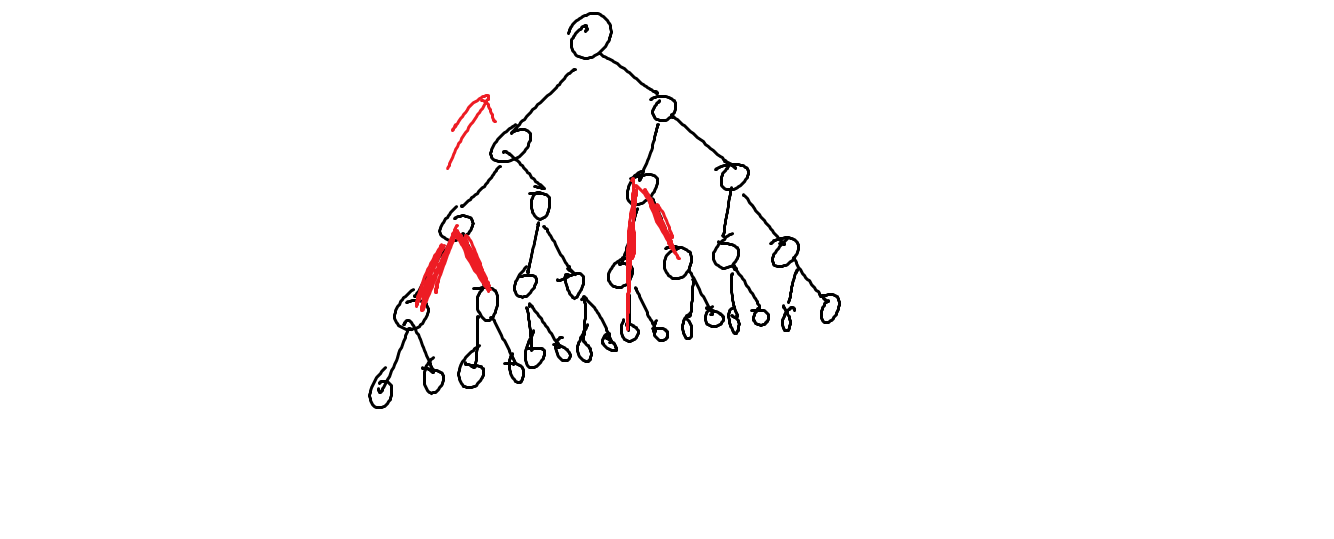
那我们一定要选择深度尽量小的点,这样尽量能够"碰到"另一条链。
所以我们这么贪心。
然后我们最后再以这个点dfs,然后一个一个判断。因为我们选了可以选到的最优点,所以这个点都凉了的话就没有其他点不凉的了。
代码如下,注意多次dfs的优秀操作:只需要变成二维就可以了。
还有理解dfs的贪心和判断距离
#include<cstdio>
#include<iostream>
#define ri register int
#define Starseven main
using namespace std;
const int N=1e5+20;
int n,m;
struct mp{
int next,to;
}f[N<<1];
int k,tail[N];
int dep[N][5],maxn,maxp;
int a[N],b[N],d[N];
int lit;
void Maketo(int from,int to){
f[++k].next=tail[from];tail[from]=k;f[k].to=to;
return ;
}
void Dfs(int x,int fa,int opt){
for(ri i=tail[x];i;i=f[i].next){
int y=f[i].to;if(y==fa) continue;
dep[y][opt]=dep[x][opt]+1;
Dfs(y,x,opt);
}
}
int Starseven(void){
cin>>n>>m;
for(ri i=1;i<n;i++){
int u,v;cin>>u>>v;
Maketo(u,v);Maketo(v,u);
}
Dfs(1,0,0);
for(ri i=1;i<=m;i++){
cin>>a[i]>>b[i]>>d[i];
if(max(0,dep[a[i]][0]+dep[b[i]][0]-d[i])>maxn) maxn=max(0,dep[a[i]][0]+dep[b[i]][0]-d[i]),maxp=i;
}
Dfs(a[maxp],0,1);Dfs(b[maxp],0,2);
for(ri i=1;i<=n;i++)
if(dep[i][1]+dep[i][2]<=d[maxp]&&(!lit||dep[lit][0]>dep[i][0])) lit=i;
Dfs(lit,0,3);
for(ri i=1;i<=m;i++){
if(dep[a[i]][3]+dep[b[i]][3]>d[i]){
cout<<"NO"<<endl;
return 0;
}
}
cout<<lit<<endl;
return 0;
}
/*
5 3
1 2
2 3
2 4
3 5
1 4 2
5 5 5
3 2 1
*/
这个东西很神奇,我在考场上根据数列的来源想出了状态转移方程,可是就做不动了。
打表无规律,还是只有实力才能解决。
看这个东西
然后
\(a(2m+1) = a(2m), a(2m) = a(2m-1) + a(m).\)
但是我们并不能干什么。
这道题说实在话,我不懂,所以我现在先留坑
这篇博客有讲.
代码没有,之后再填


