算法学习——枚举之全素组
算法说明
素数:只能被1与本身整除的整数。
1和0不是素数,也不是合数
不大于指定整数n的3个素数之和也是素数,则说这三个素数时基于整数n的全素组
例如:n=15,素数3,5,11之和3+5+11=29也为素数,所以称3,5,11是一个基于15的全数组
输入一个整数n(n不大于3000),输出基于n的全素组的个数,并输出最大全素组
算法思路
- 先取得0~n的素数,存入数组之中
- 然后使用三重枚举循环,从数组之中每次取三个,判断三个数之和是否为素数
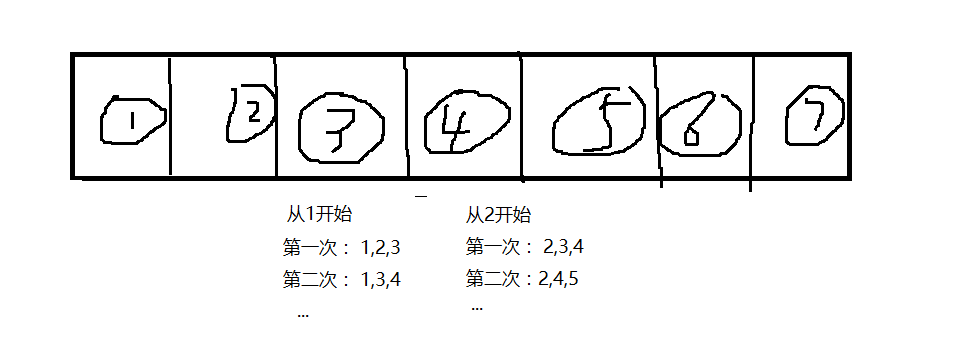
- 考虑到全素组数目较多,设置一个long长整型变量记录全素组的个数,同时,设置一个max记录全素组的最大值,三个变量用于接收最大全素组的三个数
算法实现
Scanner scaner = new Scanner(System.in);
int a = scaner.nextInt();
scaner.close();
int[] b = new int[1500];
long count =0;//全素组个数
int countsushu=0;//0~n的素数个数
//找出0到a的素数,存放在b数组中
for(int i=2,j=0;i<=a;i++){
if(panduan(i)){
b[j] = i;
countsushu++;
j++;
}
}
int max=0;
int c1=0,c2=0,c3=0;
for(int i=1;i<=countsushu-2;i++){
for(int j=i+1;j<=countsushu-1;j++){
for(int k=j+1;k<=countsushu;k++){
if(panduan(b[i]+b[j]+b[k])){
count= count+1;
if(b[i]+b[j]+b[k]>max){
c1=b[i];
c2=b[j];
c3=b[k];
max = b[i]+b[j]+b[k];
}
}
}
}
}
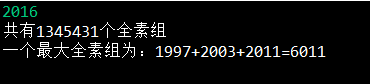
System.out.println("共有" + count+"个全素组");
System.out.println("一个最大全素组为:"+c1+"+"+c2+"+"+c3+"="+max);
}
/**
*
* @param a
* @return 通过试商法判断a是否为素数
*/
public static boolean panduan(int a){
int s = (int)Math.sqrt(a);
for(int i=2;i<=s;i++){
if(a%i==0){
return false;
}
}
return true;
}
结果