算法导论第7章

看CLRS一般把笔记写在书的margin里。Cormen的提纲也是蛮好的，适合复习。这里用的Partition方法是Lomuto Partition，不是原始的也是第1版中的Hoare Partition。后者被留作习题。快排Quicksort的时间复杂度worst-case是\Theta(n^2), 期望时间是\Theta(nlgn), 复杂度前面的常数很小，sort in place。

Descriptions of quicksort

快排是Divide-and-conquer的典范。

  • Divide: 用pivot把数组划分为两半A[p,…,q-1]和A[q+1,…,r]。前面的数组比A[q]小，后面的数组比A[q]大。
  • Conquer: 递归调用quicksort
  • Combie: 不需要，sort in place

用来划分的函数叫做PARTITION，返回下标q。

Quicksort函数

def QUICKSORT(A, p, r):
    if p < r:
        q = PARTITION(A, p, r)
        QUICKSORT(A, p, q - 1)
        QUICKSORT(A, q + 1, r)

Python美~

PARTITION函数

def PARTITION(A, p, r ):
    x = A[r ]
    i = p - 1
    for j = p to r - 1:
        if A[ j ] <= x:
            i = i + 1
            exchange A[i ] - A[ j ]

    exchange A[i + 1] - A[r ]
    return i + 1
  • PARTITION总是选取最后一个元素作为pivot，习题中可以用Median of 3优化，要求我们计算划分good split的概率提供了多少。
  • 没有优化的PARTITION有可能使得划分到的2个数组有1个为空

原文用Loop invariant证明PARTITION正确性，Initialization，Maintenance，Termination，blablabla……。时间复杂度是\Theta(n)

Performance of quicksort

对于快排的分析主要是在PARTITION的划分好坏上.

Worst-case

  • 每次划分有一个子数组是空的，这个情况只在已经按照升序排列的数组上发生。那么就只把pivot划分了出来，T(n)=T(n-1)+\Theta(n)=\Theta(n^2)。滑稽的是，insertion sort可以在O(n)时间里搞完。等下也会看到sorting-algorithms网站里也可以看到对已经差不多排序好了的数组上，插入排序快于快排。习题中要求用插入排序优化快排。

Best-case

  • 每次划分都是平均二分，T(n)=2T(n/2)+\Theta(n)=\Theta(nlgn)

Balanced partitioning

  • 既然worst-case和best-case相差这么大,那么其他的划分是很好还是很差?答案是全部是好划分.
  • Quicksort平均running time接近与best-case.书中例举了9:1的划分.还是O(nlgn)
  • 其实在递归树上,任何常数的划分都会使得树的高度是\Theta(lgn),区别只在于前面的常数

Intuition for the average case

  • 在平均的情况下,好的划分的和坏的划分是混合的.好划分之后,下面有可能是坏划分.
  • 坏划分只是使得递归树增加了一层,只是影响了nlgn后面的常数

Randomized version of quicksort

为了避免总是遇到坏的输入，我们用随机算法使这种概率下降。当然可以把整个数字全部打乱，但是更简单的是随机取一个数作为pivot

def RANDOMIZED-PARTITION(A, p, r):
    i = RANDOM(p, r )
    exchange A[r ] ↔ A[i ]
    return PARTITION(A, p, r )

如此一来，就极不可能发生worst-case了。

Analysis of quicksort

对于worst-case的严格的分析，用了递归式得到\Theta(n^2)。书中证明的是O(n^2)，习题中要证明的是\Omega(n^2)。

image

假设T(n)小于cn^2，这样把max中的两个T化成二次函数，求最大值，还是二次函数，QED。

Average-case analysis

有时候不用跟踪程序的运行来计算时间复杂度，换个角度更清楚。PARTITION总用了n次，关键是后面的元素比较次数X。注意到每对元素顶多比较1次。所以有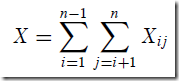image

左边取期望，右边变概率。这里原文有一点不是很严谨我也不是很明白。The probability that zi is compared to zj is the probability that either zi or z j is
the first element chosen as a pivot from Zij。为什么不考虑Z0,j。猜测是因为只涉及到Zi-Zj这几个数字就够了。X_ij=2/(j-i+1)，求和的O(nlgn)

posted @ 2011-08-05 14:38  QED  阅读(580)  评论(0)  编辑  收藏  举报