体散射初步
在说体散射之前有必要先说说渲染方程(Rendering Equation)，这个著名的方程是kajiya在1986年提出来的，其基本形式为：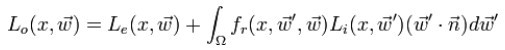
这其中Lo(x,w)表示是在点x及出射角度w上的出射光强度，Le表示在点x及出射角度
上的自发光强度，随后的一段积分则表示从外部环境中各个方向上到达点x的光强的总量。通俗地说就是:"场景中某一点的光强等于该点的自发光强度(一般光源才有自发光)加上从场景中其他点通过反射(折射)到达该点的光强"。渲染方程描述了光能在场景中的流动过程，而之前的各种全局光照和局部光照算法都是对该方程的一个近似求解。渲染方程的出现标志着全局光照的发展进入一个全新的时代，可以做出越来越逼真的效果。然而它本身也是有局限的，因为它只考虑了几何光学部分，无法表现光的衍射，干涉，偏振，色散等物理现象，也不能模拟自然界中荧光和磷光等现象。不仅如此，在一般场景中，该模型也忽略了一个重要的事实：在场景中各个物体之间也是存在物质的，它们也可能和光发生作用。
一般而言，场景中物体之间充满着空气，有限体积的空气和光的作用可以忽略不计，但是若场景中充满了微粒(比如灰尘)，那么这个对光传播的影响就不容小视了。米氏散射从物理上定义了这种光散射现象：当微粒半径的大小接近于或者大于入射光线的波长λ的时候，大部分的入射光线会沿着前进的方向进行散射，这种现象被称为米式散射。这种大微粒包括灰尘，水滴，来自污染物的颗粒物质，如烟雾，等等(wiki上的解释)。还有一种情况，就是当微粒的半径足够小（小于0.1λ），散射光线的强度与入射光线波长的四次方成反比，因此对于较短波长的散射程度要远远大于较大波长，这种散射被称为瑞利散射。瑞利散射也解释了为什么在雨过天晴或者秋高气爽的时候，天空呈现蔚蓝。因为这个时候空气中较粗微粒比较少，青蓝色光的散射显得更为突出。
为了模拟米氏散射现象(比如充满灰尘的房间或者大雾弥漫的街道)，我们必须知道一些重要的数据，这包括介质的密度，这里的介质不一定是密度均匀的，所以我们必须知道介质各处的密度函数，而这样的体数据是比较难找的，所以一种简化的模型就是假设介质各处密度相同，这就是常说的体积雾。除了介质密度外，吸收率σa和散射率σs参数也很重要，它们决定了介质对光的吸收和散射程度。相位函数p(θ)决定了当光在介质中发生散射的时候，向各个方向散射的概率。相位函数其实是一个概率密度函数，因此各个方向上几率之和要等于一。最简单的相位函数是各向同性散射函数，也就是说光朝任意方向散射的概率都是相等的。更为复杂的有Henyey-Greenstein函数，以及Schlick函数，它们的特点是，散射方向以接近光原来的前进方向和其反方向的居多，而往与光前进方向垂直平面上散射的概率最小。有了这些参数后，我们可以使用ray marching来模拟体散射。下面讲一下ray marching方法。
ray marching与ray tracing有所不同，在于前者不像后者发出射线找到交点后就直接计算交点光照，ray marching要考虑整个中间传播过程，它将整个传播过程沿途分段采样，将采样得到的数据乘以当前衰减系数后相加作为最终光强。下图展示了ray marching的计算过程：
图中由ray tracing定位到射线与球面的交点，计算出颜色color-sphere，然后沿整个射线路径取到6个点，分别计算这6个点上介质的颜色值(color1 - color6)，最后将它们分别乘以各自的衰减系数后相加得到最终颜色值。可以用如下公式概括说明这个计算过程：
，在上面例子中n=7，color7=color-sphere，ki是各自的衰减系数。在ray marching中一般每取样一次，就在之前的基础上乘上一个衰减值，这个衰减值就是介质的吸收率σa和散射率σs之和：σt=σa+σs，这也符合朗伯比尔定律对光穿过介质的描述，即在均匀介质中，透射比T的对数和介质厚度的相反数成正比。更通俗地说，就是在介质中，光强是按照传播距离指数衰减的。有了这一点，我们能更加方便地求出每个点的衰减系数，假定ray marching的采样步长取为s的话，毫无疑问光在传播了距离s后强度衰减为原来的(1-σt)，而在传播了任意距离L后，则衰减后的值可以由(1-σt)(L/s)得到，这个公式在ray marching反走样中也会用到，因为效率原因采样步长s不可能取到太小，这时，可以在s的基础上添加随机扰动，使每一次的步长不一样，那么衰减后的值也可以由公式(1-σt)(L/s)得到。需要提醒一点的是(1-σt)(L/s)仅仅是一个近似公式，这是因为步长s是一个有限值，现实中光在介质中传播的时候并不是每经过s距离才衰减一次，而是无时无刻不在衰减，也就是说s是趋于0的，朗伯比尔定律给出该模型的精确值：e-σtL。
对于ray marching每一步采样点的颜色值colori该如何计算呢？对于均匀介质而言，可以从光源向该点作射线，然后得到射线需要穿过介质的厚度，代入到之前的衰减值公式中求出衰减后的光源光强乘以介质本身的颜色就可以了。但是这样做有一个很大的问题是没有考虑到介质本身的散射，因为介质中某一点的光强不仅仅来自于光源，还可以来自介质中其他点的散射，也可以来自于场景中其他实体的漫反射。在这里，我用的是光子映射来模拟这种多重散射现象。从光源发出的光子可以在介质中被多次散射，每次散射和吸收的时候都会被记录下来，为了方便使用光子图，体散射光子应该和全局光子分开存储，这样也可以加快计算的效率。体散射光子密度估计的搜集过程是用的一个标准球体来搜集的，而之前的是用的半球，碟形搜集等。下面几幅图展示了体积雾的效果:
