排序算法系列：快速排序算法JAVA版（靠谱、清晰、真实、可用、不罗嗦版）

在网上搜索算法的博客，发现一个比较悲剧的现象非常普遍：

• 原理讲不清，混乱
• 啰嗦
• 图和文对不上
• 不可用，甚至代码还出错

为了不误人子弟耽误时间，推荐看一些靠谱的资源，如【啊哈！算法】系列：

https://www.cnblogs.com/ahalei/p/3568434.html

他是C语言实现，其实都是一样的。

 

我总结一个清晰不罗嗦版：

原理：

快速排序使用分而治之策略。下面描述递归步骤：

选择一个pivot支点值(在啊哈算法中叫“基准值”)。我们将中间元素的值作为支点值，但是它也可以是任何值，甚至它可以不存在于数组中。

第一次排序：

• 小于支点值的所有元素都到支点值的左侧
• 而大于支点值的所有元素都到支点值的右侧
• 与支点值相等的值保留。

递归，再次以支点两侧排序：对两部分进行排序，将快速排序算法递归地应用到左右部分。数组可以以不相等数量的部分划分。

算法要点：

• 有两个索引i和j，在算法的第一次排序，i 指向数组中的第一个元素，j 指向最后一个元素。
• i向前移动，直到找到一个值大于或等于支点值的元素。
• 索引j向后移动，直到找到一个值小于或等于支点值的元素。
• 如果i小于j，则它们被交换，然后进入下一个位置（i + 1），j进到前一个（j - 1）。
• 当大于j时，算法停止。

第一次排序的说明：

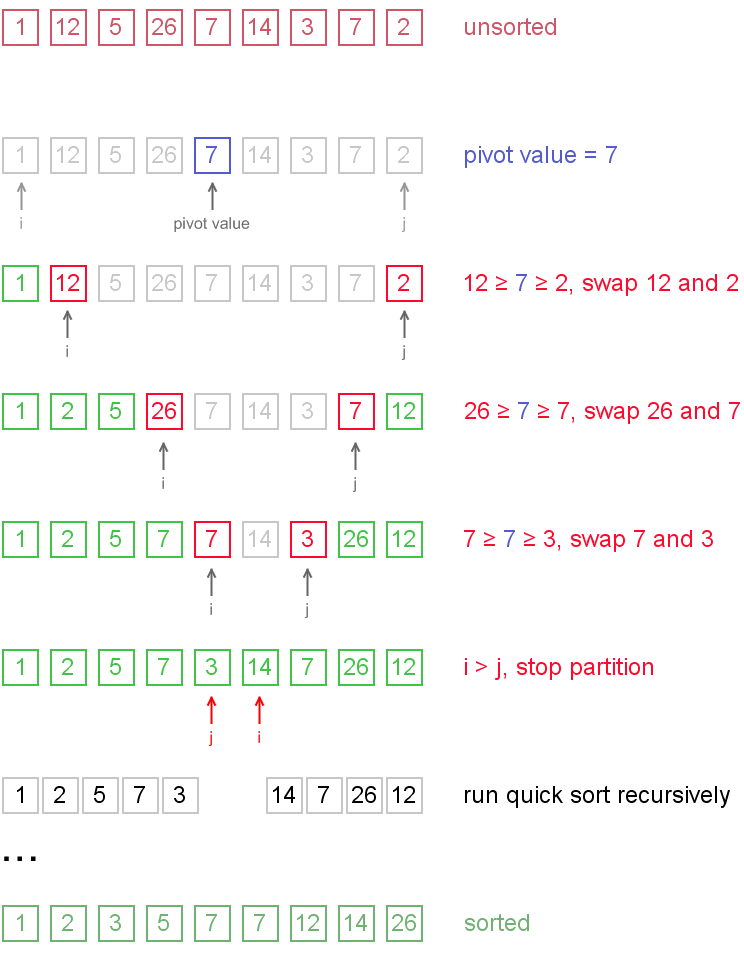
在第一轮排序之后，会进入左右的递归。依次类推。

 

复杂度分析

排序方法	时间复杂度			空间复杂度	稳定性	复杂性
	平均情况	最坏情况	最好情况
快速排序	O(nlog2n)	O(n2)	O(nlog2n)	O(log2n)	不稳定	较复杂

 

 

用JAVA实现（真实可用）：

package Sort;

public class QuickSort {
    
    
    public static void main(String[] args) {

        int arr[] = {1, 12, 5, 26, 7, 14, 3, 7, 2}; 
        int n = arr.length; 
  
        QuickSort ob = new QuickSort(); 
        ob.quickSort(arr, 0, n-1); 
        //ob.sort(arr, 0, n-1); 
  
        System.out.println("快速排序结果："); 
        printArray(arr); 
    }
    
    int partition(int arr[], int left, int right){

          int i = left, j = right;
          int tmp;
          int pivot = arr[(left + right) / 2];         
          System.out.println("pivot="+pivot+"; left="+left+"; right="+right); 

          while (i <= j) {

                while (arr[i] < pivot){
                    System.out.println("跳过，i="+i+"; arr[i]="+arr[i]+", pivot="+pivot); 
                    i++;
                }

                while (arr[j] > pivot){
                    System.out.println("跳过，j="+j+"; arr[j]="+arr[j]+", pivot="+pivot); 
                    j--;
                }


                if (i <= j) {
                      System.out.println("交换前，i="+i+", j="+j+"; arr[i]="+arr[i]+", arr[j]="+arr[j]); 

                      tmp = arr[i];
                      arr[i] = arr[j];
                      arr[j] = tmp;

                      System.out.println("交换后，i="+i+", j="+j+"; arr[i]="+arr[i]+", arr[j]="+arr[j]); 
                      System.out.println("---"); 

                      i++;
                      j--;

                }
          };         

          return i;
    }
     
    void quickSort(int arr[], int left, int right) {

          int index = partition(arr, left, right);
          if (left < index - 1){
              System.out.println("递归 左侧，left="+left+", index="+index);
              quickSort(arr, left, index - 1);
          }

          if (index < right){
              System.out.println("递归右侧，right="+right+", index="+index);
              quickSort(arr, index, right);
          }
    }
    
    static void printArray(int arr[]) 
    { 
        int n = arr.length; 
        for (int i=0; i<n; ++i) 
            System.out.print(arr[i]+" "); 
        System.out.println(); 
    } 
    

    //另一种简洁写法
     int partition1(int arr[], int low, int high) 
     { 
         int pivot = arr[high];  
         int i = (low-1); 
         for (int j=low; j<high; j++) 
         { 

             if (arr[j] <= pivot) 
             { 
                 i++; 

                 int temp = arr[i]; 
                 arr[i] = arr[j]; 
                 arr[j] = temp;

             } 
         } 
       
         int temp = arr[i+1]; 
         arr[i+1] = arr[high]; 
         arr[high] = temp; 

         return i+1; 
     } 


     void sort(int arr[], int low, int high) 
     { 
         if (low < high) 
         { 
             int pi = partition1(arr, low, high); 

             sort(arr, low, pi-1); 
             sort(arr, pi+1, high); 
         } 
     } 
}

 

调试信息：

pivot=7; left=0; right=8
跳过，i=0; arr[i]=1, pivot=7
交换前，i=1, j=8; arr[i]=12, arr[j]=2
交换后，i=1, j=8; arr[i]=2, arr[j]=12
---
跳过，i=2; arr[i]=5, pivot=7
交换前，i=3, j=7; arr[i]=26, arr[j]=7
交换后，i=3, j=7; arr[i]=7, arr[j]=26
---
交换前，i=4, j=6; arr[i]=7, arr[j]=3
交换后，i=4, j=6; arr[i]=3, arr[j]=7
---
跳过，j=5; arr[j]=14, pivot=7
递归 左侧，left=0, index=5
pivot=5; left=0; right=4
跳过，i=0; arr[i]=1, pivot=5
跳过，i=1; arr[i]=2, pivot=5
交换前，i=2, j=4; arr[i]=5, arr[j]=3
交换后，i=2, j=4; arr[i]=3, arr[j]=5
---
跳过，j=3; arr[j]=7, pivot=5
递归 左侧，left=0, index=3
pivot=2; left=0; right=2
跳过，i=0; arr[i]=1, pivot=2
跳过，j=2; arr[j]=3, pivot=2
交换前，i=1, j=1; arr[i]=2, arr[j]=2
交换后，i=1, j=1; arr[i]=2, arr[j]=2
---
递归 左侧，left=0, index=2
pivot=1; left=0; right=1
跳过，j=1; arr[j]=2, pivot=1
交换前，i=0, j=0; arr[i]=1, arr[j]=1
交换后，i=0, j=0; arr[i]=1, arr[j]=1
---
递归右侧，right=4, index=3
pivot=7; left=3; right=4
交换前，i=3, j=4; arr[i]=7, arr[j]=5
交换后，i=3, j=4; arr[i]=5, arr[j]=7
---
递归右侧，right=8, index=5
pivot=7; left=5; right=8
跳过，j=8; arr[j]=12, pivot=7
跳过，j=7; arr[j]=26, pivot=7
交换前，i=5, j=6; arr[i]=14, arr[j]=7
交换后，i=5, j=6; arr[i]=7, arr[j]=14
---
递归右侧，right=8, index=6
pivot=26; left=6; right=8
跳过，i=6; arr[i]=14, pivot=26
交换前，i=7, j=8; arr[i]=26, arr[j]=12
交换后，i=7, j=8; arr[i]=12, arr[j]=26
---
递归 左侧，left=6, index=8
pivot=14; left=6; right=7
交换前，i=6, j=7; arr[i]=14, arr[j]=12
交换后，i=6, j=7; arr[i]=12, arr[j]=14
---
快速排序
1 2 3 5 7 7 12 14 26