多项式的回归

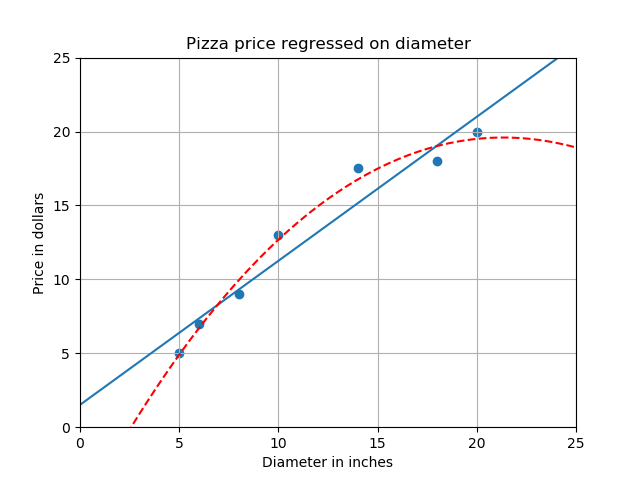
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures

X_train = [[5],[6], [8], [10], [14], [18], [20]]
y_train = [[5],[7], [9], [13], [17.5], [18], [20]]
X_test = [[6], [8], [11], [16]]
y_test = [[8], [12], [15], [18]]
regressor = LinearRegression()
regressor.fit(X_train, y_train)
xx = np.linspace(0, 26, 100)
print(xx)
#根据线性预测分析0-26的Y值
yy = regressor.predict(xx.reshape(xx.shape[0], 1))
#绘画X_Y关系直线
plt.plot(xx, yy)
quadratic_featurizer = PolynomialFeatures(degree=3)
X_train_quadratic = quadratic_featurizer.fit_transform(X_train)
X_test_quadratic = quadratic_featurizer.transform(X_test)
regressor_quadratic = LinearRegression()
regressor_quadratic.fit(X_train_quadratic, y_train)
xx_quadratic = quadratic_featurizer.transform(xx.reshape(xx.shape[0], 1))
print(xx_quadratic)
plt.plot(xx, regressor_quadratic.predict(xx_quadratic), c='r', linestyle='--')
plt.title('Pizza price regressed on diameter')
plt.xlabel('Diameter in inches')
plt.ylabel('Price in dollars')
plt.axis([0, 25, 0, 25])
plt.grid(True)
plt.scatter(X_train, y_train)
plt.show()
print(X_train)
print(X_train_quadratic)
print(X_test)
print(X_test_quadratic)
print('Simple linear regression r-squared', regressor.score(X_test, y_test))
print('Quadratic regression r-squared', regressor_quadratic.score(X_test_quadratic, y_test))