dp之沙子合并 环形沙子合并 沙子合并加强 沙子三兄弟的故事
沙子合并
沙子合并问题
问题描述：设有N堆沙子排成一排，其编号为1，2，3，…，N（N<=300）。每堆沙子有一定的数量，可以用一个整数来描述，现在要将这N堆沙子合并成为一堆，每次只能合并相邻的两堆，合并的代价为这两堆沙子的数量之和，合并后与这两堆沙子相邻的沙子将和新堆相邻，合并时由于选择的顺序不同，合并的总代价也不相同，如有4堆沙子分别为 1 3 5 2 我们可以先合并1、2堆，代价为4，得到4 5 2 又合并 1，2堆，代价为9，得到9 2 ，再合并得到11，总代价为4+9+11=24，如果第二步是先合并2，3堆，则代价为7，得到4 7，最后一次合并代价为11，总代价为4+7+11=22；问题是：找出一种合理的方法，使总的代价最小。输出最小代价。
输入：
第一行一个数N表示沙子的堆数N。
第二行N个数，表示每堆沙子的质量。
输出：
合并的最小代价
样例：
输入：
4
1 3 5 2
输出:
22
环形沙子合并
问题描述：设有N堆沙子排成一圈，其编号为1，2，3，…，N（N<=300）。每堆沙子有一定的数量，可以用一个整数来描述，现在要将这N堆沙子合并成为一堆，每次只能合并相邻的两堆，合并的代价为这两堆沙子的数量之和，合并后与这两堆沙子相邻的沙子将和新堆相邻，合并时由于选择的顺序不同，合并的总代价也不相同，如有4堆沙子分别为 1 3 5 2 我们可以先合并1、2堆，代价为4，得到4 5 2 又合并 1，2堆，代价为9，得到9 2 ，再合并得到11，总代价为4+9+11=24，如果第二步是先合并2，3堆，则代价为7，得到4 7，最后一次合并代价为11，总代价为4+7+11=22；问题是：找出一种合理的方法，使总的代价最小。输出最小代价。
输入：
第一行一个数N表示沙子的堆数N。
第二行N个数，表示每堆沙子的质量。
输出：
合并的最小代价
样例：
输入：
4
1 3 5 2
输出:
20
沙子合并加强
沙子合并问题
问题描述：设有N堆沙子排成一排，其编号为1，2，3，…，N（N<=2000）。每堆沙子有一定的数量，可以用一个整数来描述，现在要将这N堆沙子合并成为一堆，每次只能合并相邻的两堆，合并的代价为这两堆沙子的数量之和，合并后与这两堆沙子相邻的沙子将和新堆相邻，合并时由于选择的顺序不同，合并的总代价也不相同，如有4堆沙子分别为 1 3 5 2 我们可以先合并1、2堆，代价为4，得到4 5 2 又合并 1，2堆，代价为9，得到9 2 ，再合并得到11，总代价为4+9+11=24，如果第二步是先合并2，3堆，则代价为7，得到4 7，最后一次合并代价为11，总代价为4+7+11=22；问题是：找出一种合理的方法，使总的代价最小。输出最小代价。
输入：
第一行一个数N表示沙子的堆数N。
第二行N个数，表示每堆沙子的质量。
输出：
合并的最小代价以及每一步合并的方法(输出每次合并后的沙子的最小编号和最大编号)
样例：
输入：
4
13 7 6 5
输出:
60
3 4
2 4
1 4
来，先看看，找不同
总结一下第一题数据范围300，第二题范围不变，但是变成了一个环，第三题数据范围变成了2000
朴素的沙子合并算法
dp(i,j)表示把i到j这一段沙子合并成为一堆沙子，所需要的最小代价
那么一定是由某两堆合并而来的
所以dp(i,j)=min{dp(i,k)+dp(k+1,j)}+sum[j]-sum[i-1]
这样的算法O(n^3)只能过第一个吧
没事，老大被解决了
第二题是环形的
如果每个起始位置都被枚举一遍的话
就是O(n^4)，过不了，所以，我们力求一个更加高效的算法。
解决问题题的方法有两种，一种是继承，这里不讨论，还有一种是展环为链(一种解决环形dp的最佳方法)
我们复制序列一遍，将它粘贴在第一个序列的末尾，构成2n-1的序列，然后对这个序列做区间dp
所以最佳解一定是一个子问题，这下子复杂度最高(2n-1)^2,可以勉勉强强的过吧
然后第三题就麻烦了n<=2000
n^3绝对超时，肿么办呢。
这就是一套全新的理论，四边形优化
理论如下
DP的四边形优化
一、进行四边形优化需要满足的条件
1、状态转移方程如下：
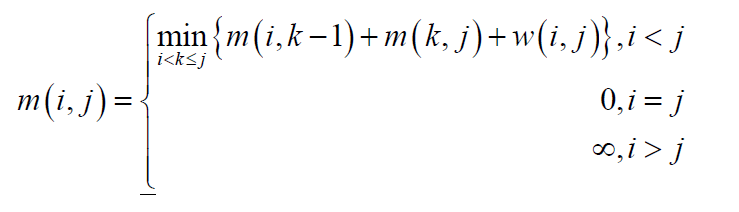
m(i,j)表示对应i,j情况下的最优值。
w(i,j)表示从i到j的代价。
例如在合并石子中：
m(i,j)表示从第i堆石子合并到j堆石子合并成一堆的最小代价。
w(i,j)表示从第i堆石子到第j堆石子的重量和。
2、函数w满足区间包含的单调性和四边形不等式
二、满足上述条件之后的两条定理
1、假如函数w满足上述条件，那么函数m 也满足四边形不等式，即
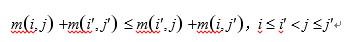
例如:
假如有：w(1, 3) + w(2, 4) £ w(2, 3) + w(1, 4)，
m(1, 3) + m(2, 4) £ m(2, 3) + m(1, 4)，
2、假如m(i, j)满足四边形不等式，那么s (i, j)单调，即：
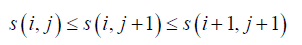
m(i,j)=min{m(i,k-1),m(k,j)}+w(i,j)(i≤k≤j)（min也可以改为max）
上述的m(i,j)表示区间[i,j]上的某个最优值。w(i,j)表示在转移时需要额外付出的代价。该方程的时间复杂度为O(N3)
下面我们通过四边形不等式来优化上述方程，首先介绍什么是“区间包含的单调性”和“四边形不等式”
1、区间包含的单调性：如果对于 i≤i'<j≤j'，有 w(i',j)≤w(i,j')，那么说明w具有区间包含的单调性。（可以形象理解为如果小区间包含于大区间中，那么小区间的w值不超过大区间的w值）
2、四边形不等式：如果对于 i≤i'<j≤j'，有 w(i,j)+w(i',j')≤w(i',j)+w(i,j')，我们称函数w满足四边形不等式。（可以形象理解为两个交错区间的w的和不超过小区间与大区间的w的和）
下面给出两个定理：
1、如果上述的 w 函数同时满足区间包含单调性和四边形不等式性质，那么函数 m 也满足四边形不等式性质
我们再定义 s(i,j) 表示 m(i,j) 取得最优值时对应的下标（即 i≤k≤j 时，k 处的 w 值最大，则 s(i,j)=k）。此时有如下定理
2、假如 m(i,j) 满足四边形不等式，那么 s(i,j) 单调，即 s(i,j)≤s(i,j+1)≤s(i+1,j+1)。
好了，有了上述的两个定理后，我们发现如果w函数满足区间包含单调性和四边形不等式性质，那么有 s(i,j-1)≤s(i,j)≤s(i+1,j) 。
即原来的状态转移方程可以改写为下式：
m(i,j)=min{m(i,k-1),m(k,j)}+w(i,j)(s(i,j-1)≤k≤s(i+1,j))（min也可以改为max）
由于这个状态转移方程枚举的是区间长度 L=j-i，而 s(i,j-1) 和 s(i+1,j) 的长度为 L-1，是之前已经计算过的，可以直接调用。
不仅如此，区间的长度最多有n个，对于固定的长度 L，不同的状态也有 n 个，故时间复杂度为 O(N^2)，而原来的时间复杂度为 O(N^3)，实现了优化！
今后只需要根据方程的形式以及 w 函数是否满足两条性质即可考虑使用四边形不等式来优化了。
以上描述状态用 m(i,j)，后文用的 dp[i][j]，所代表含意是相同的，特此说明。
以石子合并问题为例。
例如有６堆石子，每堆石子数依次为３ ４ ６ ５ ４ ２
因为是相邻石子合并，所以不能用贪心（每次取最小的两堆合并），只能用动归。（注意：环形石子的话，必须要考虑最后一堆和第一堆的合并。）
例如：一个合并石子的方案：
第一次合并 ３ ４ ６ ５ ４ ２ ->７
第二次合并 ７ ６ ５ ４ ２ ->１３
第三次合并 １３ ５ ４ ２ ->６
第四次合并 １３ ５ ６ ->１１
第五次合并 １３ １１ ->２４
总得分＝７＋６＋１１＋１３＋２４＝６１ 显然，比贪心法得出的合并方案（得分：62）更优。
动归分析类似矩阵连乘等问题，得出递推方程：
设 dp[i][j] 表示第 i 到第 j 堆石子合并的最优值，sum[i][j] 表示第 i 到第 j 堆石子的总数量。
（可以在计算开始先做一遍求所有的 sum[i]，表示求出所有第1堆到第i堆的总数量。则 sum[i][j]=sum[j]-sum[i]。这样计算比较快。）
那么就有状态转移公式：
这里 i<=k<j
普通解法需要 O（n^3）。下面使用四边形不等式进行优化。
首先判断是否符合区间单调性和四边形不等式。
i i' j j'
3 4 6 5 4 2
单调性：
w[i',j] = 4+6+5=15 w[i,j'] =3+4+6+5+4+2=24
故w[i',j] <= w[i,j'] 满足单调性
四边形不等式：
w[i,j] + w[i',j'] = (3+4+6+5) + (4+6+5+4+2) = 18+21 = 39
w[i',j] + w[i,j'] = (4+6+5) + (3+4+6+5+4+2) = 15 + 24 = 39
故 w[i,j] + w[i',j'] <= w[i',j] + w[i,j']
故石子合并可利用四边形不等式进行优化。
利用四边形不等式，将原递推方程的状态转移数量进行压缩（即缩小了k的取值范围）。
令 s[i][j]=min{k | dp[i][j] = dp[i][k-1] + dp[k][j] + w[i][j]}，即计算出 dp[i][j] 时的最优的 k 值（本例中寻优为取最小）
也可以称为最优决策时的 k 值。由于决策 s 具有单调性，因此状态转移方程中的 k 的取值范围可修改为 :
s[i,j-1] <= s[i,j] <= s[i+1,j]
边界：s[i,i] = i
因为 s[i,j] 的值在 m[i,j] 取得最优值时，保存和更新，因此 s[i,j-1] 和 s[i+1,j] 都在计算 dp[i][j-1] 以及 dp[i+1][j] 的时候已经计算出来了。
因此，s[i][j] 即 k 的取值范围很容易确定。
根据改进后的状态方程，以及 s[i][j] 的定义方程，可以很快的计算出所有状态的值。计算过程可以如下表所示（类似于矩阵连乘的打表）。
状态表（如果是环形石子合并，需要打2n*2n的表）
3 4 6 5 4 2
例如：
计算dp[1][3]，由于s[1][2]=1，s[2][3]=2，则k值的取值范围是1<=k<=2
则，dp[1][3]=min{dp(1,1)+dp(2,3)+13, dp(1,2)+dp(3,3)+13}=min{10+13, 7+13}=20，将其填到状态表。同时，由于取最优值的k等于2，则将其填到s表。
同理，可以计算其他状态表和s表中的值。
dp[2][4]=min{dp(2,2)+dp(3,4)+15, dp(2,3)+dp(4,4)+15}=min{11+15, 10+15}=25
k=3
从表中可以看出，当计算dp[2][5]的时候，由于s[ i,j-1]=s[ 2,4]=3，s[ i+1,j]=s[3,5]=3，此时k的取值范围已经限定为只有一个，大幅缩短了寻找最优解的时间。
于是乎，复杂度降到了O(n^2)
厉害吧O(∩_∩)O哈哈~
附上代码
#include<map> #include<set> #include<cmath> #include<stack> #include<queue> #include<cstdio> #include<vector> #include<cstring> #include<cstdlib> #include<iostream> #include<algorithm> #define mod 998244353 #define N 100005 #define pi acos(-1) #define inf 0x7fffffff #define ll long long using namespace std; ll read() { ll x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x*f; } int n; int a[305],sum[305]; int f[305][305]; int dp(int l,int r) { if(f[l][r]!=-1)return f[l][r]; if(l==r)return 0; int ans=inf; for(int i=l;i<r;i++) ans=min(ans,dp(l,i)+dp(i+1,r)); return f[l][r]=(ans+sum[r]-sum[l-1]); } int main() { memset(f,-1,sizeof(f)); n=read(); for(int i=1;i<=n;i++)a[i]=read(); for(int i=1;i<=n;i++)sum[i]=sum[i-1]+a[i]; printf("%d\n",dp(1,n)); return 0; }
#include<cstdio> #include<algorithm> using namespace std; int v[1001],sum[1001],f[1001][1001]; int main() { int n,mi=9999999; scanf("%d",&n); for(int i=1;i<=2*n-1;i++) for(int j=i+1;j<=2*n-1;j++) f[i][j]=999999; int p=0; for(int i=1;i<=n;i++) { scanf("%d",&v[i]); sum[i]=sum[i-1]+v[i]; } for(int i=1;i<n;i++) { v[++p]=v[i]; sum[p+n]=sum[p+n-1]+v[i]; } for(int i=2*n-1;i>=1;i--) for(int j=i+1;j<=i+n-1;j++) for(int k=i;k<j;k++) f[i][j]=min(f[i][j],f[i][k]+f[k+1][j]+sum[j]-sum[i-1]); for(int i=1;i<=n;i++) mi=min(mi,f[i][i+n-1]); printf("%d",mi); return 0; }
#include<cstdio> #include<algorithm> #define N 2000+1 #define INF 0x3fffffff using namespace std; int v[N],sum[N]; struct data{ int val,des; }; data f[N][N]; void output(int k,int i,int j); int main() { int n; scanf("%d",&n); for(int i=1;i<=n;i++) for(int j=i+1;j<=n;j++) f[i][j].val=INF; for(int i=1;i<=n;i++) { scanf("%d",&v[i]); sum[i]=sum[i-1]+v[i]; f[i][i].des=i; } for(int i=n;i>=1;i--) for(int j=i+1;j<=n;j++) { int begin=f[i][j-1].des; int end=min(j-1,f[i+1][j].des); for(int k=begin;k<=end;k++) { if(f[i][j].val>f[i][k].val+f[k+1][j].val+sum[j]-sum[i-1]) {f[i][j].des=k;f[i][j].val=f[i][k].val+f[k+1][j].val+sum[j]-sum[i-1];} } } printf("%d\n",f[1][n].val); output(f[1][n].des,1,n); // printf("%d",f[1][n].des); return 0; } void output(int k,int i,int j) { if(i==j)return; output(f[i][k].des,i,k),output(f[k+1][j].des,k+1,j); printf("%d %d\n",i,j); }
