【L53】动态规划求解最大子序和问题
Question
给定一个整数数组 nums , 找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
Anwser
当问题可以分解为彼此独立且离散子问题时,可以考虑使用动态规划来解决。
难点在于建模,即设计出动态规划解决方案(找出前后子问题的关系,体现在代码里就是计算公式)。
本题中的关系: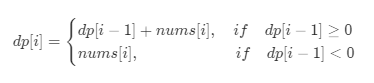
// 暴力求解,时间复杂度是O(N^3)
// func maxSubArray(nums []int) int {
// sum := nums[0]
// for i := 0; i < len(nums); i++ {
// for j := i; j < len(nums); j++ {
// var s int
// for idx := i; idx <= j; idx++ {
// s += nums[idx]
// }
// if s > sum {
// sum = s
// }
// }
// }
// return sum
// }
// 暴力求解优化,时间复杂度是O(N^2)
// 事实上,上面的代码有一些重复计算,
// 这是因为相同前缀的区间求和,即后一个区间的和=当前值+前一个区间的和。
// func maxSubArray(nums []int) int {
// sum := nums[0]
// for i := 0; i < len(nums); i++ {
// var s int
// for j := i; j < len(nums); j++ {
// s += nums[j]
// if s > sum {
// sum = s
// }
// }
// }
// return sum
// }
// 动态规划,时间复杂度是O(N)
// https://leetcode-cn.com/problems/maximum-subarray/solution/zheng-li-yi-xia-kan-de-dong-de-da-an-by-lizhiqiang/
// func maxSubArray(nums []int) int {
// if 0 == len(nums) {
// return 0
// }
// // 先计算每个子组的最大值
// idx2max := map[int]int{}
// idx2max[0] = nums[0]
// for idx:=1; idx<len(nums); idx++ {
// if idx2max[idx-1] > 0 {
// idx2max[idx] = nums[idx] + idx2max[idx-1]
// } else {
// idx2max[idx] = nums[idx]
// }
// }
// // 找到子组的最大值即全局最大值
// sum := idx2max[0]
// for _, max := range idx2max {
// if max > sum {
// sum = max
// }
// }
// return sum
// }
// 动态规划优化,降低空间复杂度
func maxSubArray(nums []int) int {
if 0 == len(nums) {
return 0
}
sum := nums[0] // 记录全局最大值
subMax := nums[0] // 只需要一个int变量保存前面子组合的最大值
for idx := 1; idx < len(nums); idx++ {
if subMax > 0 {
subMax += nums[idx]
} else {
subMax = nums[idx]
}
if subMax > sum {
sum = subMax
}
}
return sum
}
扩展
相关问题
1. 背包问题。
2. 寻找最长公共子串、最长公共子序列。
相似问题
1. 旅行商问题。
2. 集合覆盖问题。
属于NP完全问题,需要使用贪婪算法求取近似解。
作者:Standby — 一生热爱名山大川、草原沙漠、风情名城、雪域高原!
出处:http://www.cnblogs.com/standby/
本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则保留追究法律责任的权利。
出处:http://www.cnblogs.com/standby/
本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则保留追究法律责任的权利。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号