最短路径问题

前言

在上一节图的遍历算法的基础上，解决最短路径问题。

存在无权有向图如下：

v1表示起点，v9表示终点，请找出有几条路可以达到，并且最短路径是哪个？

深度优先搜索算法求解

from collections import deque

Start = "v1"
Terminal = "v9"
Q = deque()

def output():
    lst = []
    while Q:
        item = Q.popleft()
        lst.append(item)
    for item in lst:
        Q.append(item)
    print(">>>{}".format(lst))

def recurse(items, graph):
    for item in items:
        Q.append(item)          # 入栈
        if item == Terminal:    # !!!这个是递归的基线条件，递归终止的地方!!!
            output()            # 输出当前路线
            Q.pop()             # 把终点出栈
            continue
        else:
            recurse(graph[item], graph)
    Q.pop()                     # 兄弟节点都遍历完了，所以把父亲元素出栈

# depth first search
def dfs(graph):
    Q.append(Start)                     # 把起点入栈
    recurse(graph[Start], graph)        # 开始递归


if __name__ == "__main__":
    graph = {}
    graph["v1"] = ["v2", "v3", "v4"]
    graph["v2"] = ["v5", "v6"]
    graph["v3"] = ["v9"]
    graph["v4"] = ["v7", "v8"]
    graph["v5"] = ["v9", "v10"]
    graph["v6"] = ["v9"]
    graph["v7"] = []
    graph["v8"] = ["v7", "v9", "v11"]
    graph["v9"] = ["v7"]
    graph["v10"] = ["v9", "v6"]
    graph["v11"] = ["v9"]
    dfs(graph)

执行结果 ：

>>>['v1', 'v2', 'v5', 'v9']
>>>['v1', 'v2', 'v5', 'v10', 'v9']
>>>['v1', 'v2', 'v5', 'v10', 'v6', 'v9']
>>>['v1', 'v2', 'v6', 'v9']
>>>['v1', 'v3', 'v9']                             # 很明显，这个是最短路径
>>>['v1', 'v4', 'v8', 'v9']
>>>['v1', 'v4', 'v8', 'v11', 'v9']

广度优先搜索算法求解

方法一：广度优先转换为深度优先

from collections import deque

Start = "v1"
Terminal = "v9"
Q = deque()


def output():
    lst = []
    while Q:
        item = Q.popleft()
        lst.append(item)
    for item in lst:
        Q.append(item)
    lst.reverse()
    print(">>>{}".format(lst))


def recurse(items, graph):
    for item in items:
        Q.append(item)          # 入栈
        if item == Start:       # !!!这个是递归的基线条件，递归终止的地方!!!
            output()            # 输出当前路线
            Q.pop()             # 把起点出栈
            continue
        else:
            recurse(graph[item], graph)
    Q.pop()                     # 兄弟节点都遍历完了，所以把父亲元素出栈

# depth first search
def dfs(graph):
    Q.append(Terminal)                     # 把终点入栈
    recurse(graph[Terminal], graph)        # 开始递归


# breadth first search
def bfs(graph):
    q = deque()
    q += graph[Start]
    son2parent = {Start: []}
    son2parent.update(dict.fromkeys(graph[Start], [Start, ]))
    while q:
        item = q.popleft()  # first in first out
        if item != Terminal:
            q += graph[item]
            for ii in graph[item]:
                if ii not in son2parent:
                    son2parent[ii] = [item, ]
                else:
                    if item not in son2parent[ii]:
                        son2parent[ii].append(item)
    # !!!转为为使用dfs求解!!!
    dfs(son2parent)


if __name__ == "__main__":
    graph = {}
    graph["v1"] = ["v2", "v3", "v4"]
    graph["v2"] = ["v5", "v6"]
    graph["v3"] = ["v9"]
    graph["v4"] = ["v7", "v8"]
    graph["v5"] = ["v9", "v10"]
    graph["v6"] = ["v9"]
    graph["v7"] = []
    graph["v8"] = ["v7", "v9", "v11"]
    graph["v9"] = ["v7"]
    graph["v10"] = ["v9", "v6"]
    graph["v11"] = ["v9"]
    bfs(graph)

执行结果：

>>>['v1', 'v3', 'v9']
>>>['v1', 'v2', 'v5', 'v9']
>>>['v1', 'v2', 'v6', 'v9']
>>>['v1', 'v2', 'v5', 'v10', 'v6', 'v9']
>>>['v1', 'v4', 'v8', 'v9']
>>>['v1', 'v2', 'v5', 'v10', 'v9']
>>>['v1', 'v4', 'v8', 'v11', 'v9']

方法二：为了保存父子关系，所以针对每一步都生成对应的路径，并结合队列先进先出。

from collections import deque


Start = "v1"
Terminal = "v9"


def bfs(graph):
    q = deque()
    path = []
    path.append(Start)
    q.append(path)
    while q:
        path = q.popleft()
        _next = path[len(path)-1]
        if Terminal == _next:
            print(">>>{}".format(path))
        children = graph[_next]
        for child in children:
            new_path = path.copy()  # !!!important!!!
            new_path.append(child)
            q.append(new_path)


if __name__ == "__main__":
    graph = {}
    graph["v1"] = ["v2", "v3", "v4"]
    graph["v2"] = ["v5", "v6"]
    graph["v3"] = ["v9"]
    graph["v4"] = ["v7", "v8"]
    graph["v5"] = ["v9", "v10"]
    graph["v6"] = ["v9"]
    graph["v7"] = []
    graph["v8"] = ["v7", "v9", "v11"]
    graph["v9"] = ["v7"]
    graph["v10"] = ["v9", "v6"]
    graph["v11"] = ["v9"]
    bfs(graph)

执行结果：

>>>['v1', 'v3', 'v9']
>>>['v1', 'v2', 'v5', 'v9']
>>>['v1', 'v2', 'v6', 'v9']
>>>['v1', 'v4', 'v8', 'v9']
>>>['v1', 'v2', 'v5', 'v10', 'v9']
>>>['v1', 'v4', 'v8', 'v11', 'v9']
>>>['v1', 'v2', 'v5', 'v10', 'v6', 'v9']

Dijkstra算法求解

存在加权有向图如下（权重表示耗时）：

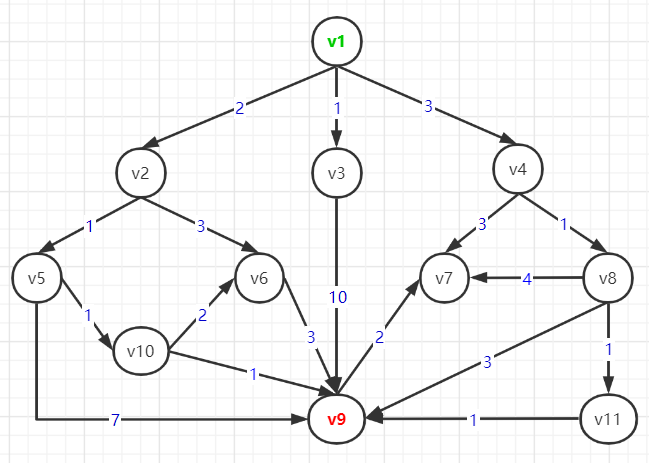
求出v1到v9走那条路径耗时最短？

Start = "v1"
Terminal = "v9"
SON2PARENT = {}
SON2COST = {}
VISITED = []


def find_lowest_cost_node(costs):
	'''
	在未处理的节点中找到开销最小的节点
	:param costs: 节点和对应开销的散列表
	:return:
	'''
	lowest_node = None
	lowest_cost = float("inf")
	for node, cost in costs.items():  # 遍历所有节点
		if node in VISITED:
			continue
		if cost < lowest_cost:
			lowest_cost = cost
			lowest_node = node
	return lowest_node

def dijkstra(graph):
	# 初始化
	infinity = float("inf")
	for node in graph.keys():
		if node in graph[Start].keys():
			SON2PARENT[node] = Start
			SON2COST[node] = graph[Start][node]
		else:
			SON2PARENT[node] = None
			SON2COST[node] = infinity
	# 遍历所有节点，依次处理该节点的所有子节点
	node = find_lowest_cost_node(SON2COST)
	while node:
		for son, weight in graph[node].items():
			cost = SON2COST[node] + weight
			if cost < SON2COST[son]:
				SON2COST[son] = cost
				SON2PARENT[son] = node
		VISITED.append(node)
		node = find_lowest_cost_node(SON2COST)

	# print(VISITED)  ['v3', 'v2', 'v4', 'v5', 'v8', 'v10', 'v6', 'v9', 'v11', 'v7']
	lst = [Terminal, ]
	parent = SON2PARENT[Terminal]
	while parent:
		lst.append(parent)
		parent = SON2PARENT[parent]
	lst.reverse()
	print("Path={} Cost={}".format(lst, SON2COST[Terminal]))


if __name__ == "__main__":
	graph = {}
	graph["v1"] = {"v2": 2, "v3": 1, "v4": 3}
	graph["v2"] = {"v5": 1, "v6": 3}
	graph["v3"] = {"v9": 10}
	graph["v4"] = {"v7": 3, "v8": 1}
	graph["v5"] = {"v9": 7, "v10": 1}
	graph["v6"] = {"v9": 3}
	graph["v7"] = {}
	graph["v8"] = {"v7": 4, "v9": 3, "v11": 1}
	graph["v9"] = {"v7": 2}
	graph["v10"] = {"v9": 1, "v6": 2}
	graph["v11"] = {"v9": 1}
	dijkstra(graph)

执行结果：

Path=['v1', 'v2', 'v5', 'v10', 'v9'] Cost=5