震惊！！！核算中心实验小学的大教练突然宣布惊天秘闻……

本周日 \(8:00 \sim 12:00\) 比赛？与直升有关？

惊 Σʕ̯•͡˔•̯᷅"ʔ。

所以是复习性质的鲜花。

从头开始吧！：

线段树

这是一个数据结构：区修区查。

是：

\______________________01______________________/
                       ||
\__________02__________/\__________03__________/
           ||                      ||
\____04____/\____05____/\____06____/\____07____/
     ||          ||          ||          ||
\__8__/\____/\____/\____/\____/\____/\____/\____/
 |   |  |  |  |  |  |  |  |  |  |  |  |  |  |  |
\16/\_/\_/\_/\_/\_/\_/\_/\_/\_/\_/\_/\_/\_/\_/\_/
23 57 22 88 254 23 4 87 24 89 224 8 22 776 43 8

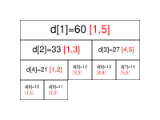
所以每个节点要有以下值：

• sum：表示和。
• lft：表示左边界。
• rgt：表示右边界。

另外每次更新会大幅度地增加时间，故设置懒标记（标记只对子树有效）：tag。

这是一个树，所以总共节点右叶子结点 \(\times 2 - 1\)，：左移一位。

点击查看代码

struct node {
    int lt, rt, lth, mid;
    ll sum, tag;
} tr[man<<2];

建树：

知道叶子结点个数 \(n\)，左孩子是 p<<1，右孩子是 p<<1|1。

设置左右边界。

• 若是单个节点（左右边界相同），则输入值；
• 否则进行下一层的建。

全部完成之后，更新本节点的值。

点击查看代码

    void build (int st, int ed, int p) {
        tr[p].lt = st, tr[p].rt = ed, 
        tr[p].lth = ed-st+1, tr[p].mid = (st+ed)>>1;
        if (st == ed) scanf("%lld", &tr[p].sum);
        else {
            build(st, (st+ed)>>1, ls);
            build(((st+ed)>>1)+1, ed, rs);
            upd;
        } return ;
    }

区间 \(\{s, e\}\) 增加：

从区间 \(\{1, n\}\) 向下递归：

• 若本段在 \(\{s, e\}\) 中，则更新标记；
• 否则查看左右子：
  • 若 \(s \leqslant\) 左子右边界（mid），则对左子递归；
  • 若 \(e \geqslant\) 右子左边界（mid+1），则对右子递归。（左右子可同时递归，并不冲突。）

全部完成之后，更新本节点的值。

点击查看代码

    void add (int st, int ed, int p, ll pls) {
        if (st<=tr[p].lt && tr[p].rt<=ed) 
            tr[p].sum += tr[p].lth*pls, tr[p].tag += pls;
        else {
            pushdown(p);
            if (st <= tr[p].mid) add(st, ed, ls, pls);
            if (tr[p].mid+1 <= ed) add(st, ed, rs, pls);
            upd;
        } return ;
    }

区间 \(\{s, e\}\) 查找：

从区间 \(\{1, n\}\) 开始向下递归：

• 若本段在 \(\{s, e\}\) 中，则返回本段和；
• 否则查看左右子：
  • 若 \(s \leqslant\) 左子右边界（mid），则对左子递归、返回和加上左子的和；
  • 若 \(e \geqslant\) 右子左边界（mid+1），则对右子递归、返回和加上右子的和。（左右子可同时递归，并不冲突。）

返回返回和。

点击查看代码

    ll ges (int st, int ed, int p) {
        if (st<=tr[p].lt && tr[p].rt<=ed) return tr[p].sum;
        pushdown(p);
        ll sum = 0;
        if (st <= tr[p].mid) sum += ges(st, ed, ls);
        if (tr[p].mid+1 <= ed) sum += ges(st, ed, rs);
        return sum;
    }

标记下沉：

懒标记并不是永久标记，所以在更新时需要下沉。

上面提到：懒标记只对子节点有效，所以只需更新子节点的值和子节点的懒标记。

在更新完后把本节点懒标记清零。

点击查看代码

    void pushdown (int p) {
        int *tg = &tr[p].tag;
        if (tg) {
            tr[ls].sum += *tg*tr[ls].lth;
            tr[rs].sum += *tg*tr[rs].lth;
            tr[ls].tag += *tg;
            tr[rs].tag += *tg;
            *tg = 0;
        } return ;
    }

例题

点击查看代码

/*
compiling in 
standard 
ide 
g++ test.cpp -o test && ./test
*/
#include <bits/stdc++.h>
#include <bits/extc++.h>
namespace {
#define filein(x) freopen(x".in", "r", stdin)
#define fileout(x) freopen(x".out", "w", stdout)
#define file(x) filein(x), fileout(x)
using namespace std;
using namespace __gnu_pbds;
#define ll long long
#define db double
#define un unsigned
#define ui un int
#define ull un ll
#define udb un db
template <typename T>
using pr = pair<T, T>;
#define pii pr<int>
#define pll pr<ll>
#define pdb pr<db>
#define fir first
#define sec second
#define mp(x, y) make_pair(x, y)
const int man = 2e6+10, mam = 1e5+10;
class SMT {
public:
struct node {
    int lt, rt, lth, mid;
    ll sum, tag;
} tr[man<<2];
#define ls (p<<1)
#define rs (p<<1|1)
#define upd tr[p].sum = tr[ls].sum+tr[rs].sum
    void build (int st, int ed, int p) {
        tr[p].lt = st, tr[p].rt = ed, 
        tr[p].lth = ed-st+1, tr[p].mid = (st+ed)>>1;
        if (st == ed) scanf("%lld", &tr[p].sum);
        else {
            build(st, (st+ed)>>1, ls);
            build(((st+ed)>>1)+1, ed, rs);
            upd;
        } return ;
    }
    void pushdown (int p) {
        ll tg = tr[p].tag;
        if (tg) {
            tr[ls].sum += tg*tr[ls].lth;
            tr[rs].sum += tg*tr[rs].lth;
            tr[ls].tag += tg;
            tr[rs].tag += tg;
            tr[p].tag = 0;
        } return ;
    }
    void add (int st, int ed, int p, ll pls) {
        if (st<=tr[p].lt && tr[p].rt<=ed) 
            tr[p].sum += tr[p].lth*pls, tr[p].tag += pls;
        else {
            pushdown(p);
            if (st <= tr[p].mid) add(st, ed, ls, pls);
            if (tr[p].mid+1 <= ed) add(st, ed, rs, pls);
            upd;
        } return ;
    }
    ll ges (int st, int ed, int p) {
        if (st<=tr[p].lt && tr[p].rt<=ed) return tr[p].sum;
        pushdown(p);
        ll sum = 0;
        if (st <= tr[p].mid) sum += ges(st, ed, ls);
        if (tr[p].mid+1 <= ed) sum += ges(st, ed, rs);
        return sum;
    }
#undef ls
#undef rs
#undef upd
} S;
}

int n, m;
void pres ();
int main () {
    pres();
    scanf("%d", &n);
    S.build(1, n, 1);
    
    scanf("%d", &m);
    for (int st, ed, i = 1; i <= m; ++ i) {
        string c;
        cin >> c;
        scanf("%d%d", &st, &ed);
        if (c == "ADD") {
            ll pls;
            scanf("%lld", &pls);
            S.add(st, ed, 1, pls);
        } else printf("%lld\n", S.ges(st, ed, 1));
    } return 0;
}

// --- 

void pres () {
#ifndef ONLINE_JUDGE
    file("test");
#endif
    return ;
}

• dp