【数据结构-树论】树状数组（BITs）
引入
观看例题
可以发现暴力妥妥 T 飞。
于是有新型数据结构：树状数组（以下简称BITs）
核心思想
为下面一堆：
若正整数 \(x\) 的二进制表示为 \(a_{k-1}a_{k-2} \dots a_1a_0\)，其中等于 \(1\) 的位是 \(\{a_{i_1}, a_{i_2}\dots a_{i_{m-1}}a_{i_m}\}\)，则正整数 \(x\) 可以被二进制分解为：
可设 \(i_1 > i_2 > \dots > i_m\)，则区间 \([1, x]\) 可以分为 \(\lceil \log x \rceil\) 个区间：
1 . 长度为 \(2^{i_1}\) 的区间：\([1, 2^{i_1}]\)
2 . 长度为 \(2^{i_2}\) 的区间：\([2^{i_1}+1, 2^{i_1}+2^{i_2}]\)
3 . 长度为 \(2^{i_3}\) 的区间：\([2^{i_1}+2^{i_2}+1, 2^{i_1}+2^{i_2}+2^{i_3}]\)
\(\dots\)
m . 长度为 \(2^{i_m}\) 的区间：\([2^{i_1}+2^{i_2}+\dots+2^{i_{m-1}}+1, 2^{i_1}+2^{i_2}+\dots+2^{i_m}]\)
以上区间有共同特点为：区间结尾为 \(R\)，其长度则为 \(lowbit(R)\)。
为什么是 \(lowbit(R)\) 呢？我也不知道 是因为 \(lowbit\) 的作用是告诉我们 \(x\) 在二进制下等于 \(1\) 的最后一个位置。
BITs 是什么以及作用
BITs 是一个维护数列前缀和的东西。对于给定的序列 \(a\)，我们可以建立一个数组 \(c\)，其中 \(c[x]\) 表示的是 \(a[x-lowbit(x)+1, x]\) 中所有数之和，即 \(\sum_{i = x-lowbit(x)+1}^x a_i\)。
事实上，你可以把 \(c\) 看作一个这样的树：
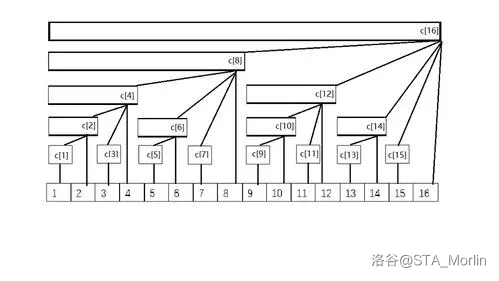
BITs 支持两个操作：单点修改 && 区间查询。
- 单点修改
如何如何，这样这样。（日常魔怔
若想将 \(a[x]\) 增加 \(k\)。
观看 \(Pic\ _1\) 可以发现，只有 \(c[x]\) 及其祖先与 \(a[x]\) 有关。
而此树深度最高只有 \(\log n\) 所以只需要挨个爬上去就可以了。
最差复杂度：\(O(\log n)\)
void add (int x, int k) {
for ( ; x <= n; x += lowbit(x)) c[x] += k;
return ;
}
- 区间查询
同上
若想求 \(a[x] \sim a[y]\)。
可以看出，\(c\) 保存的是 \(a\) 的前缀和，所以不可以直接求 \(a[x] \sim a[y]\)，但由小学数学可知：
设 \(S_x\) 为 \(a[x]\) 的前缀和。
则：
\(Q.E.D.\)
那么需要求的就是 \(S_y\) 和 \(S_{x-1}\)。
那不就是 \(c\) 储存的吗。
最差复杂度：\(O(\log n)\)
int query (int x) {
int res = 0;
for ( ; x; x -= lowbit(x)) res += c[x];
return res;
}
扩展：差分
发现这要求区间修改，单点查询。
线段树！！！
来介绍一下差分
设数组 \(a[5] = {0, 1, 6, 8, 5, 10}\)，那么差分数组 \(b[] = {1, 5, 2, -3, 5}\)
也就是说 \(b[i] = a[i]-a[i-1]\)，那么 \(a[i] = b[1]+\dots+b[i]\)。
E.G：将区间 \([2,4]\) 加 \(2\):
\(a\) 变为 \(\{0, 1, 8, 10, 7, 10\}\)，\(b\) 变为 \(\{1, 7, 2, -3, 3\}\)
可以发现，\(b\) 只有 \(b[2]\) 和 \(b[5]\) 变了，因为区间 \([2,4]\) 是同时加 \(2\) 的,所以在区间内 \(b[i]-b[i-1]\) 是不变的。
综上可得：
对区间 \([x,y]\) 进行修改，只用修改 \(b[x]\) 与 \(b[y+1]\)。
