【算法-图论】Tarjan

读音

其实 j 不发音，这个读“塔扬”。

无向图

缩点

割点

#include <bits/stdc++.h>
using namespace std;
const int man = 2e4+10, mam = 1e5+10;
class Graph {
public:
    int hed[man], len = 1;
    int nxt[mam<<1], to[mam<<1];
    void Ins (int u, int v) {
        to[++len] = v;
        nxt[len] = hed[u];
        hed[u] = len;
        return ;
    }
} G;

int n, m, rt, cnt, res;
int dfn[man], low[man], cut[man];
void tarjan (int x) {
    dfn[x] = low[x] = ++cnt;
    int f = 0;
    for (int i = G.hed[x]; i; i = G.nxt[i]) {
        int t = G.to[i];
        if (!dfn[t]) {
            tarjan(t);
            low[x] = min(low[x], low[t]);
            if (dfn[x] <= low[t]) {
                ++ f;
                if ((f>1 || x!=rt) && !cut[x]) ++ res, cut[x] = 1;
            }
        } else low[x] = min(low[x], dfn[t]);
    }
}
int main () {
#ifndef ONLINE_JUDGE
    freopen("test.in", "r", stdin);
    freopen("test.out", "w", stdout);
#endif
    scanf("%d%d", &n, &m);
    for (int u, v, i = 1; i <= m; ++ i) {
        scanf("%d%d", &u, &v);
        G.Ins(u, v), G.Ins(v, u);
    } for (int i = 1; i <= n; ++ i) if (!dfn[i]) rt = i, tarjan(i);
    printf("%d\n", res);
    for (int i = 1; i <= n; ++ i) if (cut[i]) printf("%d ", i);
    return 0;
}

一些定义

\[Pic _1 \]

有向图

一些定义

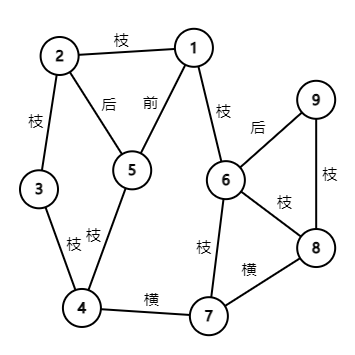
这里分为 \(4\) 种边：

1. 树枝边：搜索树上的边；
2. 前向边，即在搜索树上 \(x\) 是 \(y\) 的祖先；
3. 后向边，即在搜索树上 \(y\) 是 \(x\) 的祖先；
4. 横叉边，除以上情况外的边（满足 \(dfn_y < dfn_x\)）。

单跑

定义：每个点只取一次的点叫做单跑（不规范叫法）。

#include <bits/stdc++.h>
using namespace std;
#define pii pair<int, int>
#define mp(x, y) make_pair(x, y)
const int man = 1e4+10, mam = 1e5+10;
class Graph {
public:
    int hed[man], dis[man], len;
    int nxt[mam], to[mam];
    void Ins (int u, int v) {
        to[++len] = v;
        nxt[len] = hed[u];
        hed[u] = len;
        return ;
    }
} G, Gs;

int n, m, a, p, cnt, rec, res;
int dfn[man], low[man], ins[man], c[man];
int in[man], dis[man];
stack <int> s;
void tarjan (int x) {
    dfn[x] = low[x] = ++ cnt;
    ins[x] = 1;
    s.push(x);
    for (int i = G.hed[x]; i; i = G.nxt[i]) {
        int t = G.to[i];
        if (!dfn[t]) {
            tarjan(t);
            low[x] = min(low[x], low[t]);
        } else if (ins[t]) low[x] = min(low[x], low[t]);
    } if (dfn[x] == low[x]) {
        int y; ++ rec;
        do {
            y = s.top(); s.pop();
            ins[y] = 0, c[y] = rec;
            Gs.dis[rec] += G.dis[y];
        } while (x != y);
    } return ;
} 
void topo () {
	memset(dis, 0, sizeof(dis));
    queue <int> q;
    for (int i = 1; i <= rec; ++ i) 
    	if (!in[i]) dis[i] = Gs.dis[i], q.push(i);
    while (q.size()) {
    	int x = q.front(); q.pop();
    	res = max(res, dis[x]);
    	for (int i = Gs.hed[x]; i; i = Gs.nxt[i]) {
    		int t = Gs.to[i];
    		dis[t] = max(dis[t], dis[x]+Gs.dis[t]);
    		-- in[t];
    		if (!in[t]) q.push(t);
    	}
    } return ;
} 
int main () {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; ++ i) scanf("%d", G.dis+i);
    for (int u, v, i = 1; i <= m; ++ i) 
        scanf("%d%d", &u, &v), G.Ins(u, v);
    for (int i = 1; i <= n; ++ i) if (!dfn[i]) tarjan(i);
    for (int i = 1; i <= n; ++ i) 
        for (int j = G.hed[i]; j; j = G.nxt[j]) {
            int t = G.to[j];
            if (c[i] != c[t]) {
            	Gs.Ins(c[i], c[t]);
            	++ in[c[t]];
            }
        } 
    topo();
    printf("%d", res);
    return 0;
}

例题