【算法学习】圆方树——处理仙人掌的利器
圆方树大概分两种,一个是圆方树,一个是广义圆方树。
圆方树
这可以解决仙人掌上的问题。
任意一条边至多只出现在一条简单回路的无向连通图称为仙人掌。
很多题解将其作为无向图构建,本文将其构建为外向树,在这个问题中两种构建方式不会影响求解。
构建方式
记读入的图为原图,构建的圆方树为新图。
首先,新图保留着原图的点集,这些点记为圆点。
将原图任意一个点(实现中指定 \(1\) 号点即可)作为根节点,然后在原图跑一遍 dfs。
每当找到一个环的时候(用 tarjan 算法),将进入环的点(也就是边双的根节点)记为头节点,然后在新图上对加一个方点,并让头节点向这个方点连边,同时,方点向其它点 \(u\) 连边。
下面使原图与对应新图(圆方树)的一个例子:

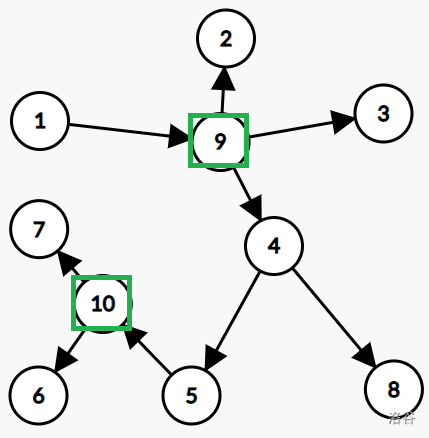
tarjan 算法变形
如何才能找到所有的简单环?为了方便,用边双连通分量求解。但是边双是不能轻易处理简单环的,比如这个图:
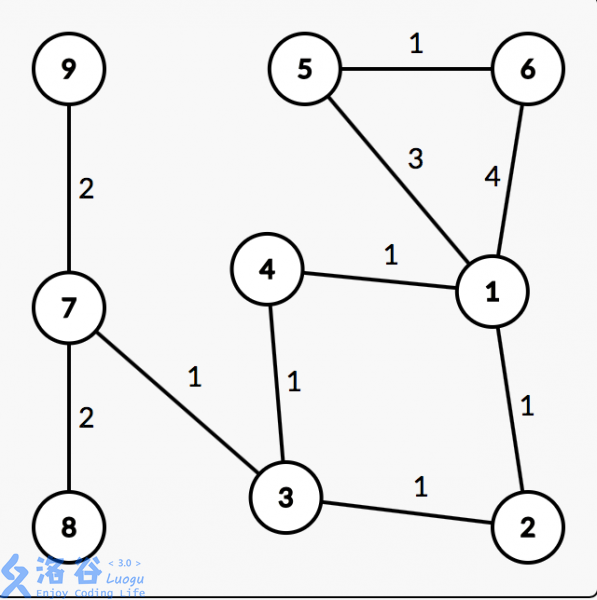
\(1,2,3,4,5,6\) 就是一个边双,但显然不是一个简单环。但是点双可以处理,至于为什么不用点双,我也不知道!反正当个板子可以用,看起来简洁。所以来改进边双:
原算法中,只要还在栈中,我们都将其看为一个边双联通分量。
但是,现在如果我们还遇到这种情况的话,就应该一个一个的处理为一个一个的简单环,而不是揉在一起。
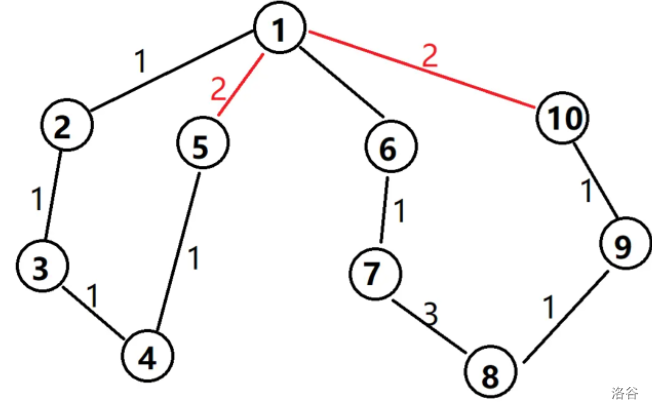
比如这张图,黑色边组成一颗搜索树,当 \(1\) 去搜儿子 \(5\) 号点时,发现 \(5\) 号点被搜过,那么就可以从 \(5\) 号点开始倒推搜索树,一直到 \(1\),这样就可以找出简单环。
all in all,看一下代码:
void build_circle(int x, int y, int z) {
for (int i = y; i != x; i = fat[i]) {
...
}
...
}
void tarjan(int u, int from) {
dfn[u] = low[u] = ++idx;
for (int p = first[u]; p; p = ed[p].next) {
int v = ed[p].e, w = ed[p].d;
if (!dfn[v]) {
fat[v] = u, fwt[v] = w, fet[v] = p;
tarjan(v, p);
low[u] = min(low[u], low[v]);
if (dfn[u] < low[v]) G[u].push_back({v, w});
}
else if (p != (from ^ 1)) low[u] = min(low[u], dfn[v]);
}
for (int p = first[u]; p; p = ed[p].next) {
int v = ed[p].e, w = ed[p].d;
if (dfn[u] < dfn[v] && fet[v] != p) build_circle(u, v, w); // 开始倒退成环
}
}
圆方树的应用
例题 1:P5236 仙人掌上任意两点间最短路
会建圆方树,但圆方树上边权咋办?每当找到一个环的时候,将进入环的点(也就是边双的根节点)记为头节点,然后在新图上对加一个方点,并让头节点向这个方点连边,边权为 \(0\),同时,方点向其它点 \(u\) 连边,边权为原图中的 \(u\) 到头节点的最短距离。
构建完圆方树后,就不难用其来求两点 \(u,v\) 最短路了:
- 当两点 \(u,v\) 的最近公共祖先为圆点时,答案就是圆方树上两点的距离,即:\(dis[u, v] = d[u] + d[v] - 2d[lca(u, v)]\)。(\(d[u]\) 为 \(u\) 到根节点的距离)
- 当两点 \(u,v\) 的最近公共祖先为方点时,记 \(u,v\) 分别与环交于 \(A,B\),注意到 \(A,B\) 在环上的距离有两种,我们需要取其中较短的,记为 \(k\),那么答案为 \(k + dis(u, A) + dis(v, B)\)。
#include <bits/stdc++.h>
using namespace std;
#define PII pair<int, int>
#define _for(i, a, b) for (int i = (a); i <= (b); i++)
#define _pfor(i, a, b) for (int i = (a); i >= (b); i--)
#define int long long
const int N = 3e5 + 5;
int n, m, q, dfn[N], low[N], idx, fat[N], fwt[N], fet[N], IDX;
int s[N], stot[N], dep[N], fa[N][20], dist[N], A, B;
int en = 1, first[N];
struct edge {
int e, d, next;
}ed[N];
vector<PII> G[N];
void add_edge(int s, int e, int d) {
en++;
ed[en].e = e, ed[en].d = d;
ed[en].next = first[s];
first[s] = en;
}
void build_circle(int x, int y, int z) {
int sum = z;
for (int i = y; i != x; i = fat[i]) {
s[i] = sum;
sum += fwt[i];
}
s[x] = stot[x] = sum;
G[x].push_back({++IDX, 0});
for (int i = y; i != x; i = fat[i]) {
stot[i] = sum;
G[IDX].push_back({i, min(s[i], sum - s[i])});
}
}
void tarjan(int u, int from) {
dfn[u] = low[u] = ++idx;
for (int p = first[u]; p; p = ed[p].next) {
int v = ed[p].e, w = ed[p].d;
if (!dfn[v]) {
fat[v] = u, fwt[v] = w, fet[v] = p;
tarjan(v, p);
low[u] = min(low[u], low[v]);
if (dfn[u] < low[v]) G[u].push_back({v, w});
}
else if (p != (from ^ 1)) low[u] = min(low[u], dfn[v]);
}
for (int p = first[u]; p; p = ed[p].next) {
int v = ed[p].e, w = ed[p].d;
if (dfn[u] < dfn[v] && fet[v] != p) build_circle(u, v, w);
}
}
void dfs(int u, int fat, int depth) {
dep[u] = depth;
for (auto e : G[u]) {
int v = e.first, w = e.second;
if (v == fat) continue;
fa[v][0] = u;
_for(i, 1, 18) fa[v][i] = fa[fa[v][i - 1]][i - 1];
dist[v] = dist[u] + w;
dfs(v, u, depth + 1);
}
}
int get_lca(int a, int b) {
if (dep[a] < dep[b]) swap(a, b);
_pfor(i, 18, 0) {
if (dep[fa[a][i]] < dep[b]) continue;
a = fa[a][i];
}
if (a == b) return a;
_pfor(i, 18, 0) {
if (fa[a][i] != fa[b][i]) {
a = fa[a][i];
b = fa[b][i];
}
}
A = a, B = b;
return fa[a][0];
}
signed main() {
cin >> n >> m >> q; IDX = n;
_for(i, 1, m) {
int u, v, w;
cin >> u >> v >> w;
add_edge(u, v, w);
add_edge(v, u, w);
}
tarjan(1, 0);
dfs(1, 0, 1);
while (q--) {
int u, v;
cin >> u >> v;
int p = get_lca(u, v);
if (p <= n) cout << dist[u] + dist[v] - dist[p] * 2 << endl;
else {
int da = dist[u] - dist[A], db = dist[v] - dist[B];
int l = abs(s[A] - s[B]);
cout << da + db + min(l, stot[A] - l) << endl;
}
}
}
例题 2:P4244 仙人掌求直径
考虑用树形 \(dp\) 的思想来做本题,枚举每一个点作为树的最高点,此时经过该点的直径应该是该点往下能到达的最长路和次长路的和。然后统计所有点作为最高点的情况,取一个最大值就是直径。
-
如果当前枚举的点是圆点,这里我们在枚举往下走的路径时,枚举的两条路径一定属于不同环,则此时圆点的所有情况一定是能对应到原图中的。
-
如果当前枚举的点是方点,意味所在简单环的点,要任选两个点往下走一条路,在加上环上这两点距离就是答案。设 \(d_i\) 表示 \(i\) 往下走的距离,那么枚举 \(i,j\) 则这条路径的长度就是 \(d_i+d_j+(i-j)\)。先破环成链(倍长),将这个看成 \(d_i+i+d_j-j\),则 \(d_i+i\) 固定,则要求 \(d_j-j\) 最大,单调队列(队尾减队头不超过环长)即可完成。
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 5e5 + 5;
int n, m, new_n, idx, fu[N], fw[N], f[N], s[N], stot[N], res, q[N];
int dfn[N], low[N], cnt, d[N];
struct node {
int v, w, id;
};
vector<node> G[N], nG[N];
void build_circle(int x, int y, int z) {
int sum = z;
for (int k = y; k != x; k = fu[k]) {
s[k] = sum;
sum += fw[k];
}
s[x] = stot[x] = sum;
nG[x].push_back({++new_n, 0, idx++});
for (int k = y; k != x; k = fu[k]) {
stot[k] = sum;
nG[new_n].push_back({k, min(s[k], sum - s[k]), idx++});
}
}
void tarjan(int u, int from) {
dfn[u] = low[u] = ++cnt;
for (auto e : G[u]) {
int v = e.v, w = e.w, id = e.id;
if (!dfn[v]) {
fu[v] = u, fw[v] = 1;
tarjan(v, id);
low[u] = min(low[u], low[v]);
if (dfn[u] < low[v]) nG[u].push_back({v, w, idx++});
}
else if (id != (from ^ 1)) low[u] = min(low[u], dfn[v]);
}
for (auto e : G[u]) {
int v = e.v, w = e.w, id = e.id;
if (dfn[u] < dfn[v] && fu[v] != u) {
build_circle(u, v, w);
}
}
}
int dfs(int u) {
int d1 = 0, d2 = 0;
for (auto e : nG[u]) {
int v = e.v, w = e.w, id = e.id;
int t = dfs(v) + w;
if (t > d1) d2 = d1, d1 = t;
else if (t > d2) d2 = t;
}
f[u] = d1;
if (u <= n) res = max(res, d1 + d2);
else {
int sz = 0;
for (auto e : nG[u]) {
int v = e.v;
d[++sz] = f[v];
}
d[++sz] = f[fu[u]];
for (int i = 1; i <= sz; i++) d[sz + i] = d[i];
int hd = 1, tl = 0;
for (int i = 1; i <= sz * 2; i++) {
while (hd <= tl && i - q[hd] > sz / 2) hd++;
if (hd <= tl) res = max(res, d[i] + d[q[hd]] + i - q[hd]);
while (hd <= tl && d[q[tl]] - q[tl] <= d[i] - i) tl--;
q[++tl] = i;
}
}
return f[u];
}
signed main() {
cin >> n >> m; new_n = n;
for (int i = 1; i <= m; i++) {
int k, x, y;
cin >> k >> x;
for (int j = 1; j <= k - 1; j++) {
cin >> y;
G[x].push_back({y, 1, idx++});
G[y].push_back({x, 1, idx++});
x = y;
}
}
tarjan(1, -1);
dfs(1);
cout << res << endl;
}
例题 3:BZOJ4316 仙人掌求最大独立集
按照常规建圆方树,只不过此时不用有边权。对于一个树边,按照常规树形 dp 转移。对于一个环,把环拆开。
比如一个环上点排成 \(1\to 5\to 4\to 3 \to 2 \to 1\)。对环上点进行 dp,环上点的点权为这个点的 \(f_{u,0/1}\)。
- 先确定 \(1\) 号点不选,那么 \(5\) 号点就没有限制。
- 再确定 \(1\) 号点选,将 \(5\) 号点选设置为非法。
具体代码:
void build_circle(int x, int y) {
// f用来辅助环上dp。当然可以用几个变量,只不过我看不懂
tot = 0;
for (int i = y; i != fa[x]; i = fa[i]) {
tot++;
f[tot][0] = dp[i][0], f[tot][1] = dp[i][1];
}
_for(i, 2, tot) {
f[i][0] += max(f[i - 1][0], f[i - 1][1]);
f[i][1] += f[i - 1][0];
}
dp[x][0] = f[tot][0]; // 先考虑不选
tot = 0;
for (int i = y; i != fa[x]; i = fa[i]) {
tot++;
f[tot][0] = dp[i][0], f[tot][1] = dp[i][1];
}
f[1][1] = -2e9;
_for(i, 2, tot) {
f[i][0] += max(f[i - 1][0], f[i - 1][1]);
f[i][1] += f[i - 1][0];
}
dp[x][1] = f[tot][1]; // 再考虑选
}
void tarjan(int u, int from) {
dfn[u] = low[u] = ++idx;
dp[u][1] = 1; dp[u][0] = 0;
for (int p = first[u]; p; p = ed[p].next) {
int v = ed[p].e;
if (!dfn[v]) {
fa[v] = u, fe[v] = p;
tarjan(v, p);
low[u] = min(low[u], low[v]);
if (dfn[u] < low[v]) {
dp[u][0] += max(dp[v][0], dp[v][1]);
dp[u][1] += dp[v][0];
}
}
else if (p != (from ^ 1)) low[u] = min(low[u], dfn[v]);
}
for (int p = first[u]; p; p = ed[p].next) {
int v = ed[p].e;
if (fe[v] != p && dfn[u] < dfn[v]) build_circle(u, v);
}
}
signed main() {
cin >> n >> m;
_for(i, 1, m) {
int u, v;
cin >> u >> v;
add_edge(u, v);
add_edge(v, u);
}
tarjan(1, 0);
cout << max(dp[1][0], dp[1][1]) << endl;
}
双倍经验:P4410 无归岛。
广义圆方树
这个东西就大为不同,我们只需要用点双就行了,而且是双向。下面的图显示了一张图对应的点双和广义圆方树形态。
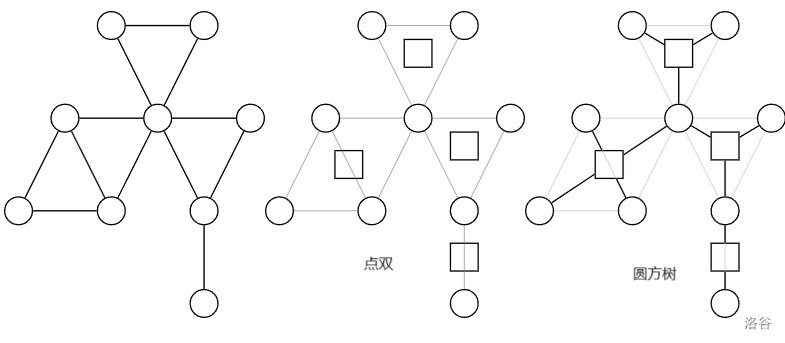
这个东西的建立也很简单,我们每找到一个点双连通分量,就建立出一个方点,向这个点双连通分量中每个点连一条无向边。下面是建立方式:
void tarjan(int u) {
dfn[u] = low[u] = ++idx;
stk.push(u);
for (auto v : G[u]) {
if (!dfn[v]) {
tarjan(v);
low[u] = min(low[u], low[v]);
if (dfn[u] <= low[v]) {
num++;
int y;
do {
y = stk.top(); stk.pop();
nG[num].push_back(y);
nG[y].push_back(num);
} while (y != v);
nG[num].push_back(u);
nG[u].push_back(num);
}
}
else low[u] = min(low[u], dfn[v]);
}
}
其实这个东西和点双缩点是互通的,点双如何缩点可以看 这篇博客(不是我写的,仅为引用)。
模板题:ABC318G
题意
给出一个有 \(n\) 个顶点和 \(m\) 条边的无向连通图 \(G\),没有重边和自环。
顶点的编号为 \(1 \sim n\),边的编号为 \(1 \sim m\),第 \(i\) 条边连接顶点 \(u_i\) 和 \(v_i\)。
给出图上三个不同的顶点 \(A,B,C\)。判断是否有从点 \(A\) 经过点 \(B\) 到点 \(C\) 的简单路径。
简单路径指路径上的点互不相同,即不重复经过同一个点。
思路
先建广义圆方树。有一个性质:对于一个点双中的两点,它们之间简单路径的并集,恰好完全等于这个点双。
写就是说:两圆点在圆方树上的路径,与路径上经过的方点相邻的圆点的集合,就等于原图中两点简单路径上的点集。证明可以用网络流。
那么 \(A,C\) 在圆方树路径上:
- 若存在点 \(B\),则有解。
- 否则,对于路径上每一个方点相邻的圆点中存在点 \(B\),也有解。
例题 \(1\):P4630 三点形成的简单路径计数
根据模板题,我们已经可以求出:给定两点,求两点简单路径上的点集的大小。将圆点权值设置为 \(-1\),将方点权值设置为相邻原点的个数。则两点间在园方树上路径的权值和就是点集大小,并且这样可以顺便减去 \(2\)(不包含 \(s,f\))。
可以直接 \(O(n^2)\) 。但是需要优化。换个角度考虑,改为统计每一个点对答案的贡献,即权值乘以经过它的路径条数,这可以通过简单的树上计数得到。
例题 \(2\):P4606
题意
给一张连通图,给一图中点集 \(S\),求这张图上有多少个点(不包含点集中的点)满足删去这个点后,给的点集 \(|S|\) 不全在一个连通分量中。
思路
先建出圆方树。
如果点集大小只有 \(2\),答案就是路径上圆点的个数。如果点集大于 \(2\),就是点集形成的极小连通子图中的圆点个数。如何求解,有一个 trick:
首先将圆点的权值转化为边权权值,即把圆点变成圆点到它父亲边上的权值。将给定点集按照 dfn 序排序,计算排序后相邻两点的边权距离和,答案就是距离和的一半,因为每条边只被经过两次。
可写成:\(\dfrac{dis(S_1,S_2)+dis(S_2,S_3)+\dots+dis(S_{n-1},S_n)+dis(S_n,S_1)}{2}\)。
注意了,只有边权距离和才能满足这个性质,点权是不行的。所以我们最开始要将点权转边权。
当 \(lca(S_1,S_n)\) 是圆点时,边权距离是算不到这个最高点的,所以此时答案加一。
例题 \(3\):CF487E:
题意
给定一个图,图上每个点有点权。要处理 \(q\) 个操作:
- C a w:表示 \(a\) 点的点权变成 \(w\)。
- A a b:表示有一个游客要从 \(a\) 点到 \(b\) 点,你要回答在两点间所有简单路径中最低点权的最低可能值。
题意
看到简单路径,立刻应该想到点双,圆方树。
根据之前模板题的性质,令方点权值为相邻圆点权值的最小值,问题转化为求路径上最小值。
但是这样遇到一个问题,如果修改一个点权,这个点周围的方点需要全部修改,一次修改最多 \(O(n)\) 复杂度,很容易被卡。
利用圆方树是一颗树的性质,对于一个方点,我们只需要维护其所有儿子圆点的权值最小值。这样查询路径上最小值还是正确的。只有一个潜在问题,如果两个点的 LCA 是方点,那么需要额外加上方点的父亲的权值。可以画图理解。
所以修改一个圆点只需要将圆点父亲的方点修改就行,儿子方点不用管。对每个方点开一个 multiset,维护所有儿子圆点的权值即可。
CF 数据非常水,用 set 都能过!!所以建议交 uoj。代码



