周赛 Round 14 2023.10.3
内部比赛链接:周赛14
预测分数:\(100+100+[20,100]+0+100+0=[320,400]\)。
实际分数: \(100+100+75+0+10+0=285\)。
挂分率:\(24\%\)。
失败原因:T3花费了较多时间思考正解,想到了线段树优化建图忘了咋打,到最后只能暴力混分。T5的dfs序打挂,不过考场上的思路和题解思路是不同的,也不知道是不是对的。T4题目都没看,看了估计也要思考很久。
总结:3个小时的时长对我来说还是短了些,只能挑题做,有时候还会挑很难的题,把简单题放掉了。以后要先看完所有题面,每道题都先思考 5 min。熟练掌握学过的知识点,保证能顺利打出板子。
然后老师说 abc 都才 100 分钟,3个小时岂不是绰绰有余,我真滴是醉了,这个比赛 C 题(每次基本都是 CF 1800 左右的题,ABC233G都出过)都比 abc E 难吧。
A. 修改序列 modify

考虑且最小值和最大值之差最多为 \(1\),那么最终序列肯定呈 均分状态。又因为最终序列总和不变,则可以算出均分状态下的每一个值。然后每个数 \(A_i\) 则变成距离它最近的最终序列值就行。
B. 表示法 knuth
模拟题,注意需要在除了前缀 ten 之外的所有前缀前放一个 one.
C. 魔力塔 tower

自学过线段树优化建图,考试时不知道为什么忘了咋写。于是开始思考单调队列优化 dp,未果。然后只能打暴力,忘了咋打 bfs(?),感觉 dijstra 好写,骗了 75。 \(\color{white}{CF786B}\)
线段树优化建图基本操作:点到区间连边。
如下图,若节点 \(8\) 向区间 \([3,7]\) 连边。
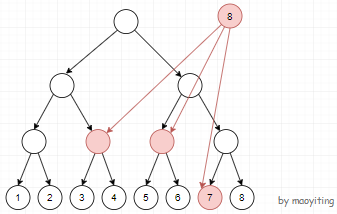
别忘了,还有区间到点连边的操作(这道题没有),如果这两个操作混合起来,则需要建立出树和入树。
代码:code
这道题还有暴力过题做法,但我不会。
D. 卡牌 card
理一理题面,初始有两堆牌,初始时第一堆只有一张牌 \(S\),第二堆的牌从上到下由输入给出。
有孵化和克制两种规则,孵化 \(C,A,B\) 表示若第一堆上面那张为 \(C\),可以将其变成两张 \(A,B\)。克制 \(A,B\) 表示若第一堆为最上面为 \(A\),第二堆最上面为 \(B\),两张牌可以同时消失。
区间 dp,第一堆的牌其实可以消除一段连续区间。设 \(dp_{i,j,x}\) 表示第一堆的牌 \(x\) 能否消除第二堆牌从上到下 \([i,j]\)。
通过给出的克制关系,初始化所有 \(dp_{i,i,j}\)。
通过给出的孵化关系进行转移:\(dp_{i,j,x}=dp_{i,k,A}\&dp_{k+1,j,B}\),表示牌 \(x\) 孵化成 \(A,B\),分别来克制 \([i,k]\) 和 \([k+1,j]\)。
答案就是 \(dp_{1,n,S}\)。
#include <bits/stdc++.h>
using namespace std;
const int N = 105;
#define PII pair<char, char>
int n1, n2, dp[N][N][N];
char a[N];
vector<PII> vis[N];
vector<char> vs[N];
int main() {
cin >> n1 >> n2;
for (int i = 1; i <= n1; i++) {
cin >> a;
vs[a[0] - 'A'].push_back(a[3]);
}
for (int i = 1; i <= n2; i++) {
cin >> a;
vis[a[0] - 'A'].push_back({a[3] - 'A', a[4] - 'A'});
}
while (cin >> (a + 1)) {
int n = strlen(a + 1);
memset(dp, 0, sizeof dp);
for (int i = 1; i <= n; i++) {
for (int j = 0; j < 26; j++) {
for (auto v : vs[j]) {
if (v == a[i]) dp[i][i][j] = 1;
}
}
}
for (int len = 2; len <= n; len++) {
for (int i = 1; i + len - 1 <= n; i++) {
int j = i + len - 1;
for (int k = i; k < j; k++) {
for (int c = 0; c < 26; c++) {
for (auto v : vis[c]) {
int c1 = v.first, c2 = v.second;
dp[i][j][c] |= dp[i][k][c1] & dp[k + 1][j][c2];
}
}
}
}
}
if (dp[1][n]['S' - 'A']) puts("YES");
else puts("NO");
memset(a, 0, sizeof a);
}
}
E. 生长树 tree CF383C
对于每个节点打上 lazy,若当前层数为奇数则加,为偶数则减。询问时层数若为奇数加上打过的 lazy,为偶数减去打过的 lazy。这样就实现了层数奇偶加减。
for (int i = 1; i <= m; i++) {
int op, x, val;
scanf("%lld%lld", &op, &x);
if (op == 1) {
scanf("%lld", &val);
if (dep[x] % 2 == 1) modify(1, in[x], out[x], val);
else modify(1, in[x], out[x], -val);
}
else {
if (dep[x] % 2 == 1) cout << a[x] + query(1, in[x], in[x]) << endl;
else cout << a[x] - query(1, in[x], in[x]) << endl;
}
}
F. 单词 word CF543C
它与众不同的定义是:一个字符串只要有一个字符和其他字符串都不同,就算与众不同。
那么要把一个字符串改成与众不同就两种情况:
- 把这个字符改成与众不同。
- 把其他所有与这个字符相同的字符串这个位置改成与众不同。
处理出 与这个字符串第 \(j\) 个位置相同的所有字符串 集合,计算出把 与这个字符串第 \(j\) 个位置相同的所有字符串 改成与众不同的代价。
你会发现第二种操作虽然代价高,但是更改后与这个字符串这个位置相同的所有字符串全都变成与众不同的了。
#pragma GCC optimize(2)
#pragma GCC optimize(3)
#include <bits/stdc++.h>
using namespace std;
const int N = 22;
int n, m;
char a[N][N];
int c[N][N], dp[1 << N], val[N][N], bas[N][N];
int main() {
while (cin >> n >> m) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cin >> a[i][j];
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cin >> c[i][j];
}
}
memset(bas, 0, sizeof bas);
memset(val, 0, sizeof val);
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
int res = 0, maxn = 0;
for (int k = 0; k < n; k++) {
if (a[i][j] == a[k][j]) {
bas[i][j] += (1 << k); // base表示与这个位置相同的集合
res += c[k][j];
maxn = max(maxn, c[k][j]);
}
}
val[i][j] = res - maxn; // val表示更改代价
}
}
// 状态压缩 dp
// dp_{i}表示使i集合中所有字符串独一无二的最小代价
memset(dp, 0x3f, sizeof dp);
dp[0] = 0;
for (int i = 0; i < (1 << n); i++) {
for (int j = 0; j < n; j++) {
if (!(i & (1 << j))) {
for (int k = 0; k < m; k++) {
dp[i | (1 << j)] = min(dp[i | (1 << j)], dp[i] + c[j][k]);
dp[i | bas[j][k]] = min(dp[i | bas[j][k]], dp[i] + val[j][k]);
}
}
}
}
cout << dp[(1 << n) - 1] << endl;
}
}
复杂度 \(O(n\times m\times 2^n)\),不是特别优秀。但是发现转移顺序不影响答案,所以随便找一个 j 满足 !(i & (1 << j)) 就行。



