并查集论文
它是一种轻量型的简单数据结构，可以动态维护若干个集合，并支持合并查询。
find(x)，查询一个元素属于哪一个集合。merge(x, y)，合并两个集合。
为了实现这个数据结构，我们采用 一个代表 表示这个集合。就是说，每个集合选择一个固定的元素，作为整个集合的代表。
我们需要定义归属关系的表示方法。第一种思路是维护一个数组 \(p\)，\(p[x]\) 保存元素所在集合代表。这种方法可以快速查询元素的归属集合，但在合并时需要更改大量元素的 \(p\) 值，效率低下。第二种思路是使用一个树形结构存储每个集合，树上每个节点都是一个元素，树根是集合的代表元素。整个并查集实际上是个森林（若干棵树）。依然可以维护一个数组 \(p\) 来记录这个森林，用 \(p[x]\) 保存 \(x\) 的父节点。同时，树根的 \(p\) 值是他自己。这样一来，合并两个集合时，只需要连接两个树根（令其中的一个树根为另一个树根的子节点，即 \(p[root_1]=root_2\)）。不过在查询元素的归属时，需要从该元素开始通过 \(p\) 存储的值不断访问父节点，直达树根。为了提高效率，采用路径压缩的方法。
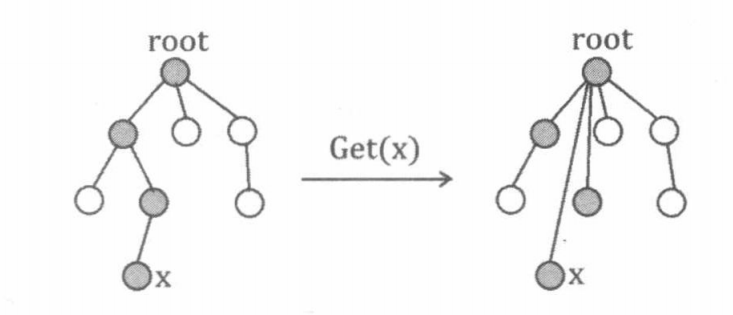
如上图所示，在每次执行 \(\rm find\) 操作的同时，把访问过的每个节点（也就是查询元素的全部祖先）都直接指向树根。 采用路径压缩后的并查集，每次 find 均摊复杂度 \(O(\log n)\)。
例题 1：亲戚
若某个家族人员过于庞大，要判断两个是否是亲戚，确实还很不容易，现在给出某个亲戚关系图，求任意给出的两个人是否具有亲戚关系。
思路
查找两个人是否具有亲戚关系等价与两个元素是否在同一个集合。若 \(x\) 和 \(y\) 具有亲戚关系只需要 \(\rm {merge(x,y)}\)。
例题 2：程序自动分析
题面见上，略。
思路
我们知道，等号具有传递性，如 \(a=b,b=c\) 则 \(a=c\)。
若 \(e=1\)，即题目所给约束条件 \(x=y\)，则将 \(x\) 和 \(y\) 两个元素合并，即 \(\rm merge(x,y)\)。也就若两个元素在同一个集合中，即两元素相等。
若 \(e=0\)，即题目所给约束条件 \(x\neq y\)，则看 \(x\) 和 \(y\) 两个元素是否在同一个集合中，若在同一个集合中，则 \(x=y\)，与题目所给约束条件矛盾。
此题数据范围较大，需要进行离散化处理。
\(\Large 拓：扩展域与边带权并查集\)
并查集实际上是由若干棵树组成的森林，我们可以在树中的每条边记录一个权值，即维护一个数组 \(d\)，用 \(d[x]\) 保存节点 \(x\) 到父节点 \(d[x]\) 之间的边权。在每次路径压缩后，每个访问过的节点都会直接指向树根，如果我们同时更新这些节点的 \(d\) 值，就可以利用路径压缩过程来统计每个节点到树根之间的路径上的一些信息。这就是所谓的 边带权 并查集。
例题 3：银河英雄传说
题面如上，略。
思路
我们可以把每一列看作一个集合，用并查集维护。最初， \(N\) 个战舰构成 \(N\) 个独立的集合。
在没有路径压缩的情况下，\(p[x]\) 就表示排在第 \(x\) 号战舰前面的那个战舰的编号。一个集合的代表就是位于最前边的战舰。另外，让树上每条边权值带 \(1\)，这样树上两点之间的距离减一就是二者直接间隔的战舰数量。
在考虑路径压缩的情况下，我们额外建立一个数组 \(d\)，\(d_x\) 记录战舰 \(x\) 与 \(p[x]\) 之间的边的权值。在路径压缩把 \(x\) 直接指向树根的同时，我们把 \(d[x]\) 更新为 \(x\) 到树根的路径上的所有边权之和。参考代码
在收到一个合并指令时，把 \(x\) 的树根作为 \(y\) 树根的子节点，连接的新边的权值应该设置为合并之前集合 \(y\) 的大小（根据题意，集合 \(y\) 的全部战舰都排在集合 \(x\) 之前）。
在收到的查询指令时，执行 \(\rm find (x)\) 与 \(\rm find (y)\) ，若二者返回值相同，则在同一列中。因为此时 \(x\) 和 \(y\) 都已经指向树根，所以 \(d[x]\) 保存了位于 \(x\) 之前的战舰数量，\(d[y]\) 保存了位于 \(y\) 之前的战舰数量。二者之差的绝对值再减 \(1\)，就是 \(x\) 和 \(y\) 之间间隔的战舰数量。
例题 4：\(\rm Parity \ game\)
题面如上，略。
思路
如果我们用 \(sum\) 数组表示序列 \(S\) 的前缀和，那么在每个回答中：
- \(S[l\sim r]\) 有偶数个 \(1\)，等价于 \(sum[l-1]\) 与 \(sum[r]\) 奇偶性相同。
- \(S[l\sim r]\) 有奇数个 \(1\)，等价于 \(sum[l-1]\) 与 \(sum[r]\) 奇偶性不同。
注意，这里没有求出 \(sum\) 数组，我们只是把 \(sum\) 看作变量。此题跟程序自动分析异常类似。不同的是本题的传递关系不只一种。
- 若 \(x_1\) 与 \(x_2\) 奇偶性相同，\(x_2\) 与 \(x_3\) 奇偶性也相同，那么 \(x_1\) 与 \(x_3\) 奇偶性相同。这跟程序自动分析中的等于关系一样。
- 若 \(x_1\) 与 \(x_2\) 奇偶性相同，\(x_2\) 与 \(x_3\) 奇偶性不同，那么 \(x_1\) 与 \(x_3\) 奇偶性不同。
- 若 \(x_1\) 与 \(x_2\) 奇偶性不同，\(x_2\) 与 \(x_3\) 奇偶性也不同，那么 \(x_1\) 与 \(x_3\) 奇偶性相同。
为了解决众多的传递关系，第一种方法是使用"边带权”"的并查集。
若边权 \(d[x]\) 为 \(0\)，表示 \(x\) 与 \(p[x]\) 奇偶性相同；为 \(1\)，表示 \(x\) 与 \(p[x]\) 奇偶性不同。在路径压缩时，对 \(x\) 到树根路径上的所有边权做异或运算，即可得到 \(x\) 与树根的奇偶性关系。
对于每个问题，设在离散化后 \(l-1\) 和 \(r\) 的值分别是 \(x\) 和 \(y\)，设 \(ans\) 表示该问题的回答 （\(0\) 代表偶数个，\(1\) 代表奇数个）。
