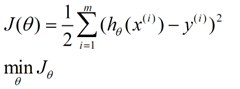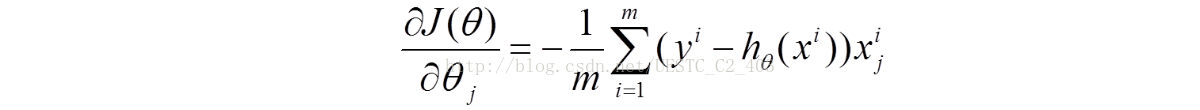批量梯度下降,随机梯度下降,小批量梯度下降
在机器学习领域中,梯度下降的方式有三种,分别是:批量梯度下降法BGD、随机梯度下降法SGD、小批量梯度下降法MBGD,并且都有不同的优缺点。
下面我们以线性回归算法(也可以是别的算法,只是损失函数(目标函数)不同而已,它们的导数的不同,做法是一模一样的)为例子来对三种梯度下降法进行比较。
1. 线性回归
假设 特征 和 结果 都满足线性。即不大于一次方。这个是针对 收集的数据而言。
收集的数据中,每一个分量,就可以看做一个特征数据。每个特征至少对应一个未知的参数。这样就形成了一个线性模型函数,向量表示形式:
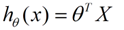
这个就是一个组合问题,已知一些数据,如何求里面的未知参数,给出一个最优解。 一个线性矩阵方程,直接求解,很可能无法直接求解。有唯一解的数据集,微乎其微。
基本上都是解不存在的超定方程组。因此,需要退一步,将参数求解问题,转化为求最小误差问题,求出一个最接近的解,这就是一个松弛求解。
求一个最接近解,直观上,就能想到,误差最小的表达形式。仍然是一个含未知参数的线性模型,一堆观测数据,其模型与数据的误差最小的形式,模型与数据差的平方和最小:
2. 参数更新
对目标函数进行求导,导数如下:
利用梯度下降跟新参数,参数更新方式如下:
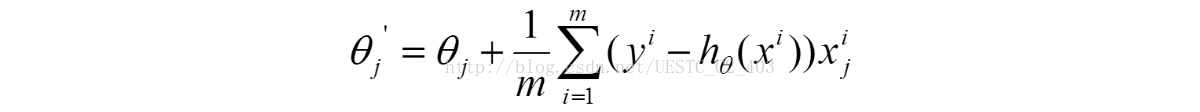
3. 批量梯度下降法(Batch Gradient Descent,简称BGD)是梯度下降法最原始的形式,它的具体思路是在更新每一参数时都使用所有的样本来进行更新,也就是方程(1)中的m表示样本的所有个数。
优点:全局最优解;易于并行实现;
缺点:当样本数目很多时,训练过程会很慢。
4. 随机梯度下降法:它的具体思路是在更新每一参数时都使用一个样本来进行更新,也就是方程(1)中的m等于1。每一次跟新参数都用一个样本,更新很多次。如果样本量很大的情况(例如几十万),那么可能只用其中几万条或者几千条的样本,就已经将theta迭代到最优解了,对比上面的批量梯度下降,迭代一次需要用到十几万训练样本,一次迭代不可能最优,如果迭代10次的话就需要遍历训练样本10次,这种跟新方式计算复杂度太高。
但是,SGD伴随的一个问题是噪音较BGD要多,使得SGD并不是每次迭代都向着整体最优化方向。
优点:训练速度快;
缺点:准确度下降,并不是全局最优;不易于并行实现。
从迭代的次数上来看,SGD迭代的次数较多,在解空间的搜索过程看起来很盲目。
5.小批量梯度下降法(Mini-batch Gradient Descent,简称MBGD):它的具体思路是在更新每一参数时都使用一部分样本来进行更新,也就是方程(1)中的m的值大于1小于所有样本的数量。为了克服上面两种方法的缺点,又同时兼顾两种方法的有点。
6.三种方法使用的情况:
如果样本量比较小,采用批量梯度下降算法。如果样本太大,或者在线算法,使用随机梯度下降算法。在实际的一般情况下,采用小批量梯度下降算法。