2020杭电多校第一场题解
2020 Multi-University Training Contest 1
1004 Distinct Sub-palindromes
\(n\geq3\) 时考虑形如 \(abcabcabc\cdots\) 的构造。
刚开题时读成了可以不连续的字串，所以就变成了一道爆难的组合数题目。
直到第三名队友解救我们于水火之中（读题人背大锅）
#include<bits/stdc++.h>
using namespace std;
int main() {
int t;
scanf("%d", &t);
while (t--) {
int n;
scanf("%d", &n);
if (n <= 3) {
int ans = 1;
while (n--) ans *= 26;
printf("%d\n", ans);
}
else {
int ans = 26 * 25 * 24;
printf("%d\n", ans);
}
}
return 0;
}
1005 Fibonacci Sum
原题 \(ZOJ3774\) 。公式推导可以参考该题的博客。
比赛时尝试退了很久的公式，其实后来公式已经对了，但我们出现了对指数取模的奇妙操作，于是爆炸了，直到最后才发现。
本以为之后会记住这个问题，但没想到后面的比赛也出现了相同操作，只能说取模形成了肌肉记忆，让人哭笑不得。
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e5;
int f[N + 5], inv[N + 5];
const int P = 1e9 + 9;
void init() {
f[0] = 1;
for (int i = 1; i <= N; ++i)
f[i] = 1ll * i * f[i - 1] % P;
inv[N] = qpow(f[N], P - 2);
for (int i = N - 1; i >= 0; --i)
inv[i] = (i + 1ll) * inv[i + 1] % P;
}
inline int C(int n, int m) {
return 1ll * f[n] * inv[m] % P * inv[n - m] % P;
}
inline int qpow(int a, int b) {
int res = 1;
for (; b; b >>= 1) {
if (b & 1) res = res * a % P;
a = a * a % P;
}
return res;
}
signed main() {
ios::sync_with_stdio(false);
cin.tie(nullptr); cout.tie(nullptr);
int T; cin >> T;
const int sqr5 = 616991993;
const int inv2 = qpow(2, P - 2);
const int invsqr5 = qpow(sqr5, P - 2);
const int a = (sqr5 + 1ll) * inv2 % P, b = (P + 1 - sqr5) * inv2 % P;
const int invb = qpow(b, P - 2);
while (T--) {
int n, c, k;
cin >> n >> c >> k;
int q = qpow(qpow(b, k), c);
int dq = qpow(1ll * a * invb % P, c);
int da1 = -q;
int qn = qpow(q, n);
int dqn = qpow(dq, n);
int ans = 0;
int sign = k & 1 ? -1 : 1;
for (int i = 0; i <= k; ++i) {
int bin = C(k, i);
int s = sign * (q == 1 ? n % P : q * (qn - 1ll) % P * qpow(q - 1, P - 2) % P);
ans = (ans + 1ll * s * bin % P) % P;
q = 1ll * q * dq % P;
qn = 1ll * qn * dqn % P;
sign = -sign;
}
ans = 1ll * ans * qpow(invsqr5, k) % P;
ans = (ans + P) % P;
cout << ans << '\n';
}
return 0;
}
1006 Finding a MEX
每个点记录修改的时间和查询时间，用 \(\text{set}\) 维护 \(\text{mex}\)，同时用 \(\text{vector}\) 数组维护每次查询的修改。对于每个点单独维护，对于每个儿子，若修改次数大于查询次数，\(\text{vector}\) 用查询在修改中查找；若查询次数大于修改次数，\(\text{vector}\) 用修改在查询中查找。然后维护 \(\text{set}\) 求 \(\text{mex}\) 。
#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> pii;
const int maxn = 1e5 + 5;
int a[maxn];
vector<int> E[maxn], G[maxn];
vector<pii> S[maxn], V[maxn];
set<int> res;
int res_cnt[maxn];
vector<pii> out;
int main()
{
int t;
scanf("%d", &t);
for (int l = 1; l <= t; l++) {
int n, m;
scanf("%d%d", &n, &m);
out.resize(0);
for (int i = 1; i <= n; i++) {
E[i].resize(0);
G[i].resize(0);
S[i].resize(0);
}
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
S[i].push_back(make_pair(0, a[i]));
}
int u, v;
for (int i = 1; i <= m; i++) {
scanf("%d%d", &u, &v);
E[u].push_back(v);
E[v].push_back(u);
}
int q, type;
scanf("%d", &q);
for (int i = 1; i <= q; i++) {
scanf("%d", &type);
if (type == 1) {
scanf("%d%d", &u, &v);
S[u].push_back(make_pair(i, v));
} else {
scanf("%d", &u);
G[u].push_back(i);
}
}
for (int i = 1; i <= n; i++) {
res.clear();
for (int j = 0; j <= (int)E[i].size(); j++) {
res_cnt[j] = 0;
res.insert(j);
}
for (int j = 0; j < (int)E[i].size(); j++) {
if (a[E[i][j]] <= (int)E[i].size() && res_cnt[a[E[i][j]]]++ == 0) {
res.erase(a[E[i][j]]);
}
}
G[i].push_back(0X3f3f3f3f);
for (int j = 0; j < (int)E[i].size(); j++) {
vector<pii>& cnt = S[E[i][j]];
if ((int)G[i].size() < (int)cnt.size()) {
int pre = a[E[i][j]];
for (int k = 0; k < (int)G[i].size() - 1; k++) {
int p = upper_bound(cnt.begin(), cnt.end(), make_pair(G[i][k], 0)) - cnt.begin();
int now = cnt[p - 1].second;
if (pre != now) {
V[k].push_back(make_pair(pre, now));
pre = now;
}
}
} else {
int preval = a[E[i][j]], pretime = -1, nowval = preval;
for (int k = 1; k < (int)cnt.size(); k++) {
int p = upper_bound(G[i].begin(), G[i].end(), cnt[k].first) - G[i].begin();
if (pretime != p && p != (int)G[i].size() - 1) {
if (pretime != -1)
V[pretime].push_back(make_pair(preval, nowval));
preval = nowval;
pretime = p;
nowval = cnt[k].second;
} else if (p == pretime && p != (int)G[i].size() - 1)
nowval = cnt[k].second;
}
if (pretime != -1 && pretime != (int)G[i].size() - 1)
V[pretime].push_back(make_pair(preval, nowval));
}
}
for (int j = 0; j < (int)G[i].size() - 1; j++) {
for (auto it : V[j]) {
if (it.first <= (int)E[i].size() && --res_cnt[it.first] == 0)
res.insert(it.first);
}
for (auto it : V[j])
if (it.second <= (int)E[i].size() && res_cnt[it.second]++ == 0)
res.erase(it.second);
out.push_back(make_pair(G[i][j], *res.begin()));
V[j].resize(0);
}
}
sort(out.begin(), out.end());
for (auto it : out)
printf("%d\n", it.second);
}
return 0;
}
1008 Integral Calculus
\[\begin{gather*}\int_0^{\infty} \frac{x^{-2k-1}}{e^{\frac{1}{x}}-1}dx\\倒带换得到\int_0^{\infty}\frac{x^{2k-1}}{e^x-1}dx\\\frac{1}{e^x-1}=\sum_{i=1}^{\infty}e^{-ix}\\交换求和积分次序\sum_{i=1}^{\infty}\int_0^{\infty} x^{2k-1}e^{-ix}dx\\后面的积分用ix换元计算得到为\frac{\Gamma(2k-1)}{i^{2k}}\\这里2k-1是整数，所以最后的结果为\sum_{i=1}^{\infty}\frac{(2k-1)!}{i^{2k}}=(2k-1)!\zeta(2k)\\对于偶数处的黎曼zeta函数用伯努利数求\zeta(2n)=\frac{(-1)^{n-1}B_{2n}(2\pi)^n}{2(2n!)}\end{gather*}
\]
#include <bits/stdc++.h>
using namespace std;
const int M = 1 << 19;
const int P = 1e9 + 9;
namespace FFT {
using DB = long double;
using LL = long long;
struct CP {
DB x, y;
CP(DB x = 0, DB y = 0) : x(x), y(y) {}
CP operator+(const CP& rhs) const {
return { x + rhs.x, y + rhs.y };
}
void operator+=(const CP& rhs) {
x += rhs.x, y += rhs.y;
}
CP operator-(const CP& rhs) const {
return { x - rhs.x, y - rhs.y };
}
CP operator*(const CP& rhs) const {
return { x * rhs.x - y * rhs.y, x * rhs.y + y * rhs.x };
}
CP operator!() const {
return { x, -y };
}
} f[M], g[M], h[M], p_w[M + 1];
int bit_inv[M];
void init() {
DB alpha = acos(-1) / M * 2;
for (int i = 0; i <= M; i++) p_w[i] = CP(cos(alpha * i), sin(alpha * i));
for (int i = 0, j = 1; j < M; j++) {
for (int k = M >> 1; (i ^= k) < k; k >>= 1);
bit_inv[j] = i;
}
}
void FFT(CP* A, int N, int D = 1) {
for (int j = 1, i, d = __builtin_ctz(M / N); j < N - 1; j++) if ((i = (bit_inv[j] >> d)) < j) swap(A[i], A[j]);
for (int n = 1, m = M / 2 * D; n < N; m /= 2, n <<= 1) {
for (int i = 0; i < N; i += n << 1) {
CP* w = (D == 1 ? p_w : p_w + M), * a = A + i, * b = A + i + n;
for (int j = 0; j < n; j++, a++, b++, w += m) {
CP x = *w * *b;
*b = *a - x;
*a += x;
}
}
}
if (D != 1) for (int i = 0; i < N; i++) A[i].x /= N, A[i].y /= N;
}
void conv(int* A, int* B, int* C, int N, int MOD) {
if (N <= 64) {
static int temp[64];
memset(temp, 0, sizeof(int) * N);
for (int i = 0; i < N; i++) {
for (int j = 0; j < N - i; j++) temp[i + j] = (temp[i + j] + 1LL * A[i] * B[j]) % MOD;
for (int j = N - i; j < N; j++) temp[i + j - N] = (temp[i + j - N] + 1LL * A[i] * B[j]) % MOD;
}
memcpy(C, temp, sizeof(int) * N);
return;
}
for (int i = 0; i < N; i++) f[i] = CP(A[i] >> 15, A[i] & 32767);
FFT(f, N);
for (int i = 0; i < N; i++) g[i] = CP(B[i] >> 15, B[i] & 32767);
FFT(g, N);
for (int i = 0; i < N; i++) {
int j = i ? N - i : 0;
h[i] = ((f[i] + !f[j]) * (!g[j] - g[i]) + (!f[j] - f[i]) * (g[i] + !g[j])) * CP(0, 0.25);
}
FFT(h, N, -1);
for (int i = 0; i < N; i++) C[i] = (LL(h[i].x + 0.5) % MOD << 15) % MOD;
for (int i = 0; i < N; i++) {
int j = i ? N - i : 0;
h[i] = (!f[j] - f[i]) * (!g[j] - g[i]) * CP(-0.25, 0) + CP(0, 0.25) * (f[i] + !f[j]) * (g[i] + !g[j]);
}
FFT(h, N, -1);
for (int i = 0; i < N; i++) C[i] = (C[i] + LL(h[i].x + 0.5) + ((LL(h[i].y + 0.5) % MOD) << 30)) % MOD;
}
};
int f[M], g[M], r[M], p[M], a[M], b[M], c[M], ans[M];
namespace Inverse {
int A0[M];
void inverse(int* A, int* B, int N, int P) {
memset(B + 1, 0, sizeof(int) * (N - 1));
B[0] = 1;
for (int n = 2, h = 1; n <= N; h <<= 1, n <<= 1) {
FFT::conv(A, B, A0, n, P);
for (int i = 0; i < h; i++) A0[i] = 0;
FFT::conv(A0, B, A0, n, P);
for (int i = h; i < n; i++) ((B[i] = P - A0[i]) == P) && (B[i] = 0);
}
}
};
int modExp(int a, int n, int p) {
int ret = 1;
for (; n; n >>= 1, a = 1LL * a * a % p) if (n & 1) ret = 1LL * ret * a % p;
return ret;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
FFT::init();
for (int i = 0; i < M; i++) {
f[i] = i == 0 ? 1 : f[i - 1] * 1LL * i % P;
r[i] = i <= 1 ? i : r[P % i] * 1LL * (P - P / i) % P;
g[i] = i == 0 ? 1 : g[i - 1] * 1LL * r[i] % P;
}
for (int i = 0; i < M; i++) b[i] = g[i + 1];
Inverse::inverse(b, a, M, P);
int ncase;
for (cin >> ncase; ncase--; ) {
int n; cin >> n;
int zeta4n = 1ll * a[4 * n] % P * modExp(2, 4 * n - 1, P) % P;
int zeta2n = 1ll * a[2 * n] % P * modExp(2, 2 * n - 1, P) % P;
if ((n - 1) & 1)zeta2n = -zeta2n;
if ((2 * n - 1) & 1)zeta4n = -zeta4n;
zeta2n = 1ll * zeta2n * f[2 * n - 1] % P;
zeta4n = 1ll * zeta4n * f[4 * n - 1] % P;
zeta2n = 1ll * zeta2n * zeta2n % P;
int ans = (1ll * zeta4n * modExp(zeta2n, P - 2, P) % P);
cout << (P + ans % P) % P << '\n';
}
return 0;
}
1009 Leading Robots
将整个过程化简为分析直线交点的过程，统计出现在最上方的直线交点的数量。首先对直线进行排序，然后根据单调性加入单调队列。需要注意有重叠的线段需要排除，还有多线共交点需要特殊处理。
#include<bits/stdc++.h>
#define ll long long
#define mod 998244353
#define maxn 100000
using namespace std;
struct cv {
int x, y;
bool operator < (const cv& b) const {
return (x == b.x ? y > b.y : x > b.x);
}
}a[maxn];
ll n1[maxn], n2[maxn];
int main() {
int t;
scanf("%d", &t);
while (t--) {
int n;
scanf("%d", &n);
for (int i = 0; i < n; i++) scanf("%d %d", &a[i].x, &a[i].y);
sort(a, a + n);
vector<int> b(n + 1);
int ans = 0;
n1[0] = 0, n2[0] = 1;
stack<int> vp;
vp.push(0);
int ma = a[0].y;
for (int i = 1; i < n; i++) {
int las = vp.top();
if (a[i].x == a[las].x && a[i].y == a[las].y)
b[i] = b[las] = 1;
else if (ma >= a[i].y) b[i] = 1;
else {
ma = max(ma, a[i].y);
while (!vp.empty()) {
las = vp.top();
n1[i] = a[las].x - a[i].x, n2[i] = a[i].y - a[las].y;
if (n1[las] * n2[i] >= n2[las] * n1[i]) {
b[las] = 1;
vp.pop();
}
else {
vp.push(i);
break;
}
}
}
}
for (int i = 0; i < n; i++)
if (b[i] == 0)
ans++;
printf("%d\n", ans);
}
return 0;
}
1010 Math is Simple
\[\begin{aligned}\sum_{1\leq a <b \leq n\\gcd(a,b)=1\\\ \ a+b\geq n}{\frac{1}{ab}}\\\end{aligned}
\]
\[\begin{gather*}考虑a+b=n 的情况设为g(n)=\sum_{a=1}^{n}\frac{1}{a(n-a)}[gcd(a,n-a)=1][a<n-a]\\由更相减损法得到条件相当于[gcd(a,n)=1],对\frac{1}{a(n-a)}裂项:\\\frac{1}{a(n-a)}=\frac{1}{n}(\frac{1}{a}+\frac{1}{n-a})\\再有对称性得到:g(n)=\frac{1}{2n}(2(\sum_{a=1}^{n}\frac{1}{a}[gcd(a,n)=1])-\sum_{a=n-a}[gcd(a,n)=1]))=\\\frac{1}{n}((\sum_{a=1}^{n}\frac{1}{a}[gcd(a,n)=1])-[n=2])\\后面是经典反演式子:g(n)=\frac{1}{n}\sum_{d|n}\mu(d)h(\frac{n}{d})\frac{1}{d}\\记原式为f(n),考虑f(n)-f(n-1)=\sum_{1\leq a<b=n\\gcd(a,b)=1}\frac{1}{ab}-\sum_{1\leq a<b\leq n-1\\gcd(a,b)=1\\a+b=n-1}\frac{1}{ab}=g(n)-g(n-1)\\f(n)-f(2)=g(n)-g(2)\\毒瘤出题人卡常数卡的一匹不允许预处理\mu还要求2^{\omega(n)}枚举因子\end{gather*}
\]
#include<bits/stdc++.h>
using namespace std;
const int N = 1e8;
const int M = 1e4 + 1000;
const int P = 998244353;
int inv[N + 10], p[N / 3];
bool vis[N + 10];
const int inv2 = P - P / 2;
int main() {
int T;
inv[1] = 1;
for (int i = 2; i <= N; i++)
inv[i] = (0ll + P - P / i) * inv[P % i] % P;
for (int i = 2; i <= N; i++)
inv[i] = (inv[i] + inv[i - 1]) % P;
int m = 0;
for (int i = 2; i <= M; i++) {
if (!vis[i])p[++m] = i;
for (int j = 1; j <= m && p[j] * i <= M; j++) {
vis[p[j] * i] = true;
if (i % p[j] == 0)break;
}
}
scanf("%d", &T);
while (T--) {
int n;
scanf("%d", &n);
if (n == 2) {
printf("%d\n", inv2);
continue;
}
int ans = 0;
vector<int> fac;
int y = n;
ans = inv[n];
for (int i = 1; p[i] * p[i] <= n; i++) {
if (n % p[i] == 0) {
fac.push_back(p[i]);
while (n % p[i] == 0)n /= p[i];
}
}
if (n != 1) fac.push_back(n);
vector<int> d(1 << fac.size());
d[0] = 1;
for (int st = 1; st < d.size(); st++) {
int x = d[st] = d[st - (st & (-st))] * fac[__builtin_ctz(st)];
int miu = (__builtin_popcount(st) & 1 ? -1 : 1);
int z = y / x;
ans = (ans + 1ll * miu * (inv[x] - inv[x - 1]) * inv[z]) % P;
}
ans = (1ll * ans * (inv[y] - inv[y - 1]) + inv2) % P;
ans = (ans + P) % P;
printf("%d\n", ans);
}
return 0;
}
1011 Minimum Index
根据 \(\text{Lyndon}\) 分解，最后一段 \(\text{Lyndon}\) 分解为最小的后缀，那么在计算 \(\text{Lyndon}\) 分解时，计算最后一段 \(\text{Lyndon}\) 分解的坐标就可以了。
根据 \(\text{Duval}\) 算法 分成三种情况，其中 \(k < j\)
当 \(s[k] > s[j]\) ，分解子串，同时 \(j\) 的最小后缀是 \(i\)
当 \(s[k] = s[j]\)，不影响近似简单性，自增同时 \(j\) 的最小后缀由循环节可以推得为 \(ans[k] + j - k\)
比赛时并不知道还有 \(\text{Lyndon}\) 分解这种操作，但如果属性模板，确实就是道模板题。
只能说是我们知识点还不足，覆盖面不够广。
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int maxn = 1e6 + 5;
const LL mod = 1e9 + 7;
char s[maxn];
int ans[maxn];
int main()
{
int t;
scanf("%d", &t);
while (t--) {
scanf("%s", s + 1);
int len = strlen(s + 1);
int i = 1;
ans[1] = 1;
while (i <= len) {
int j = i + 1, k = i;
while (j <= len && s[k] <= s[j]) {
if (s[k] < s[j]) {
k = i;
ans[j] = i;
} else {
ans[j] = ans[k] + j - k;
k++;
}
j++;
}
while (i <= k)
i += j - k;
ans[j] = i;
}
LL base = 1112, fac = 1, res = 0;
for (int i = 1; i <= len; i++) {
res = (res + fac * ans[i]) % mod;
fac = fac * base % mod;
}
printf("%lld\n", res);
}
return 0;
}
1012 Mow
分成人力更便宜和除草机更便宜两类讨论，这里只讨论用除草机更划算的情况。先跑出凸包，然后将凸包的所有边向内部移动 \(r\) 个单位，求出这个新得到的凸多边形的核，算出这个面积的对应的权值。注意到除草机的可覆盖面积是这个多边形核加上一堆矩形和扇形，不难计算出总面积是：
\[\begin{gather*}S=S_核+C_核r+\pi r^2\end{gather*}
\]
可参考下图，蓝色多边形是原多边形（红色）的核：
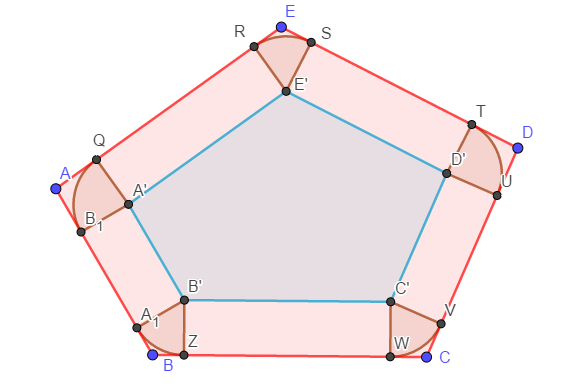
比赛时没读这题，只能说没想到。主要还是前期被卡死了，后期开题也很有问题。
#include<bits/stdc++.h>
#define db double
using namespace std;
const db eps = 1e-7;
const db pi = acos(-1.0);
int sign(db k) {
if (k > eps) return 1;
else if (k < -eps) return -1;
return 0;
}
struct point {
db x, y;
point() {}
point(db x_, db y_) :x(x_), y(y_) {}
point operator + (const point& k) const { return point(k.x + x, k.y + y); }
point operator - (const point& k) const { return point(x - k.x, y - k.y); }
point operator * (db k) const { return point(x * k, y * k); }
point operator / (db k1) const { return point(x / k1, y / k1); }
point turn90() { return point(-y, x); } // 逆时针方向旋转 90 度
db len() { return sqrt(x * x + y * y); } // 向量长度
db dis(point rhs) { return ((*this) - rhs).len(); }
point unit() { db d = len(); return point(x / d, y / d); }
bool operator < (const point& k) const {
return x == k.x ? y < k.y : x < k.x;
}
bool getP() const { return sign(y) == 1 || (sign(y) == 0 && sign(x) == -1); }
};
db cross(point k1, point k2) { return k1.x * k2.y - k1.y * k2.x; }
db dot(point k1, point k2) { return k1.x * k2.x + k1.y * k2.y; }
db rad(point k1, point k2) { return atan2(cross(k1, k2), dot(k1, k2)); }
int compareangle(point k1, point k2) {
return k1.getP() < k2.getP() || (k1.getP() == k2.getP() && sign(cross(k1, k2)) > 0);
}
struct line {
point p[2];
line() {}
line(point k1, point k2) { p[0] = k1, p[1] = k2; }
point& operator [] (int k) { return p[k]; }
point dir() { return p[1] - p[0]; }
bool include(point k) { return sign(cross(p[1] - p[0], k - p[0])) > 0; }
line push(db len) { // 向外（左手边）平移 len 个单位
point delta = (p[1] - p[0]).turn90().unit() * len;
return line(p[0] - delta, p[1] - delta);
}
};
bool parallel(line k1, line k2) { return sign(cross(k1.dir(), k2.dir())) == 0; }
bool sameDir(line k1, line k2) { return parallel(k1, k2) && sign(dot(k1.dir(), k2.dir())) == 1; }
bool operator < (line k1, line k2) {
if (sameDir(k1, k2)) return k2.include(k1[0]);
return compareangle(k1.dir(), k2.dir());
}
point getLL(point k1, point k2, point k3, point k4) { // 两直线交点
db w1 = cross(k1 - k3, k4 - k3), w2 = cross(k4 - k3, k2 - k3);
return (k1 * w2 + k2 * w1) / (w1 + w2);
}
point getLL(line k1, line k2) { return getLL(k1[0], k1[1], k2[0], k2[1]); }
bool checkpos(line k1, line k2, line k3) { return k3.include(getLL(k1, k2)); }
vector<point> convexHull(vector<point>A, int flag = 1) { // flag=0 不严格 flag=1 严格
int n = A.size(); vector<point>ans(n + n);
sort(A.begin(), A.end()); int now = -1;
for (int i = 0; i < A.size(); i++) {
while (now > 0 && sign(cross(ans[now] - ans[now - 1], A[i] - ans[now - 1])) < flag) now--;
ans[++now] = A[i];
}
int pre = now;
for (int i = n - 2; i >= 0; i--) {
while (now > pre&& sign(cross(ans[now] - ans[now - 1], A[i] - ans[now - 1])) < flag)
now--;
ans[++now] = A[i];
}
ans.resize(now);
return ans;
}
vector<line> getHL(vector<line>& L) { // 求半平面交 逆时针方向存储
sort(L.begin(), L.end());
deque<line> q;
for (int i = 0; i < (int)L.size(); ++i) {
if (i && sameDir(L[i], L[i - 1])) continue;
while (q.size() > 1 && !checkpos(q[q.size() - 2], q[q.size() - 1], L[i])) q.pop_back();
while (q.size() > 1 && !checkpos(q[1], q[0], L[i])) q.pop_front();
q.push_back(L[i]);
}
while (q.size() > 2 && !checkpos(q[q.size() - 2], q[q.size() - 1], q[0])) q.pop_back();
while (q.size() > 2 && !checkpos(q[1], q[0], q[q.size() - 1])) q.pop_front();
vector<line> ans;
for (int i = 0; i < q.size(); ++i) ans.push_back(q[i]);
return ans;
}
db polygonArea(vector<point> P) {
point top = P[0];
db ans = 0.0;
for (int i = 1; i < P.size() - 1; ++i)
ans += cross(P[i] - top, P[i + 1] - P[i]);
return fabs(0.5 * ans);
}
db polygonCircumference(vector<point> p) {
db ans = 0.0;
int n = p.size();
for (int i = 0; i < n; ++i)
ans += fabs(p[i].dis(p[(i + 1) % n]));
return ans;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr); cout.tie(nullptr);
int t; cin >> t;
while (t--) {
int n, r, a, b;
cin >> n >> r >> a >> b;
vector<point> p(n);
for (auto& i : p) cin >> i.x >> i.y;
p = convexHull(p);
n = (int)p.size();
db s = polygonArea(p);
if (a <= b) {
db ans = s * a;
cout << fixed << setprecision(12) << ans << '\n';
}
else {
vector<line> l(n);
for (int i = 0; i < n; ++i) {
l[i] = line(p[i], p[(i + 1) % n]);
l[i] = l[i].push(-r);
}
vector<line> res = getHL(l);
if ((int)res.size() < 3) {
db ans = a * s;
cout << fixed << setprecision(12) << ans << '\n';
continue;
}
vector<point> pp((int)res.size());
for (int i = 0; i < (int)res.size(); ++i)
pp[i] = getLL(res[i], res[(i + 1) % (int)res.size()]);
db ps = polygonArea(pp) + pi * r * r + polygonCircumference(pp) * r;
db ans = (s - ps) * a + ps * b;
cout << fixed << setprecision(12) << ans << '\n';
}
}
return 0;
}
这场比赛相当爆炸，主要还是队伍配合不够，加上还没有熟悉比赛，读题也很成问题。
希望以后相同的问题不会再出现。
