2020, XIII Samara Regional Intercollegiate Programming Contest 题解
2020, XIII Samara Regional Intercollegiate Programming Contest 题解
A. Array's Hash
题意:\(Vasya\) 发明了一种新的散列函数,给定一个数组 \(a_n\) ,这个散列函数每次将数组中的前两个元素替换为一个值为 \(a_2 - a_1\) 的元素,直到只剩下一个元素,得到的这个元素即为新的哈希值。现在有 \(q\) 次询问,每次询问前该数组都先执行一个区间加操作,然后询问该数组的哈希值。
分析:这个新的哈希值就是 \(a_n-a_{n-1}+a_{n-2}-a_{n-3}+a_{n-4}\cdots\) ,因此我们直接将奇偶下标各看作一个数组进行操作即可。实际上可以 \(O(n)\) 做,不过这里偷懒直接复制了个树状数组板子。
#include <bits/stdc++.h>
#define int long long
#define SIZE 1000010
using namespace std;
int n;
namespace FenwickTree {
int ta1[SIZE], ta2[SIZE], tb1[SIZE], tb2[SIZE];
int lowbit(int x) { return x & (-x); }
void add(int pos, int x, int t[]) { // 单点修改
for (; pos <= n; pos += lowbit(pos)) {
t[pos] += x;
}
}
void add(int l, int r, int x, int t1[], int t2[]) { // [l, r] 区间+x
add(l, x, t1);
add(r + 1, -x, t1);
add(l, l * x, t2);
add(r + 1, -x * (r + 1), t2);
}
int query_presum(int pos, int t[]) { // 单点查询,即对差分数组求前缀和
int ans = 0;
for (; pos > 0; pos -= lowbit(pos)) {
ans += t[pos];
}
return ans;
}
int query_sum(int l, int r, int t1[], int t2[]) { // 区间修改下的区间查询
int p1 = l * query_presum(l - 1, t1) - query_presum(l - 1, t2);
int p2 = (r + 1) * query_presum(r, t1) - query_presum(r, t2);
return p2 - p1;
}
}
using namespace FenwickTree;
signed main() {
ios::sync_with_stdio(false);
cin.tie(nullptr); cout.tie(nullptr);
cin >> n;
for (int i = 1; i <= n; ++i) {
int x; cin >> x;
int pos = (i + 1) >> 1;
if (i & 1) add(pos, pos, x, ta1, ta2);
else add(pos, pos, x, tb1, tb2);
}
int q; cin >> q;
for (int i = 1; i <= q; ++i) {
int l, r, v;
cin >> l >> r >> v;
int la = ((l + 1) >> 1) + !(l & 1), ra = (r + 1) >> 1;
int lb = (l >> 1) + (l & 1), rb = r >> 1;
if (la <= ra) add(la, ra, v, ta1, ta2);
if (lb <= rb) add(lb, rb, v, tb1, tb2);
int ans = query_sum(1, n, ta1, ta2) - query_sum(1, n, tb1, tb2);
if (n & 1) cout << ans << '\n';
else cout << -ans << '\n';
}
}
B. Bonuses on a Line
题意:数轴上有 \(n\) 个点,坐标为 \((x_i,0)\) ,你从原点开始能够移动 \(t\) 个单位距离,询问最多能够经过几个点。
分析:将正点和负点分开存,然后枚举我们到达的左端点(右端点同理),二分搜索从该端点向右走最多能够经过几个正点。
#include <bits/stdc++.h>
#define ll long long
using namespace std;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr); cout.tie(nullptr);
ll n, t; cin >> n >> t;
vector<ll> pos, neg;
for (int i = 0; i < n; ++i) {
ll x; cin >> x;
if (x < 0) neg.emplace_back(-x);
else pos.emplace_back(x);
}
sort(neg.begin(), neg.end());
sort(pos.begin(), pos.end());
ll ans = 0;
for (int i = 0; i < neg.size(); ++i) {
if (neg[i] > t) break;
ll maxd = t - neg[i] - neg[i];
ll res = 0;
if (maxd > 0) res = upper_bound(pos.begin(), pos.end(), maxd) - pos.begin();
ans = max(ans, i + res + 1);
}
for (int i = 0; i < pos.size(); ++i) {
if (pos[i] > t) break;
ll maxd = t - pos[i] - pos[i];
ll res = 0;
if (maxd > 0) res = upper_bound(neg.begin(), neg.end(), maxd) - neg.begin();
ans = max(ans, i + res + 1);
}
cout << ans;
}
C. Manhattan Distance
题意:给定二维平面上 \(n\) 个点,求曼哈顿距离第 \(k\) 近的点对。
分析:二分搜索答案,计数时有一个技巧:因为距离某个点 \((x,y)\) 的曼哈顿距离不超过 \(d\) 的点可以看作在一个旋转了 \(90°\) 的正方形中,该正方形顶点分别为 \((x-d,y);(x,y-d);(x+d,y);(x,y+d)\) ,处理较为复杂;因此,我们不妨直接将坐标系旋转 \(90°\) ,那样所有距离某个点 \((x,y)\) 的曼哈顿距离不超过 \(d\) 的点都可以看作在一个顶点分别为 \((x-\frac{d}{2},y-\frac{d}{2});(x-\frac{d}{2},y+\frac{d}{2});(x+\frac{d}{2},y+\frac{d}{2});(x+\frac{d}{2},y-\frac{d}{2})\) 的正方形中,我们可以利用树状数组快速计数。时间复杂度 \(O(n\log n \log 4e8)\) 。
#include <bits/stdc++.h>
#include <random>
#define ll long long
#define mp make_pair
#define SIZE 100010
using namespace std;
ll n, k;
namespace FenwickTree {
int t[SIZE];
int lowbit(int x) { return x & (-x); }
void add(int pos, int x, int t[]) { // 单点修改
for (; pos <= n; pos += lowbit(pos)) {
t[pos] += x;
}
}
int query_presum(int pos, int t[]) { // 单点查询
int ans = 0;
for (; pos > 0; pos -= lowbit(pos)) {
ans += t[pos];
}
return ans;
}
}
using namespace FenwickTree;
ll check(int d, vector<pair<int, int> >& p, vector<int>& y) {
ll res = 0;
memset(t, 0, sizeof(t));
for (int i = 0, j = 0; i < n; ++i) {
while (j < i && p[i].first - p[j].first > d) {
add(lower_bound(y.begin(), y.end(), p[j].second) - y.begin() + 1, -1, t);
j++;
}
res += query_presum(upper_bound(y.begin(), y.end(), p[i].second + d) - y.begin(), t);
res -= query_presum(lower_bound(y.begin(), y.end(), p[i].second - d) - y.begin(), t);
add(lower_bound(y.begin(), y.end(), p[i].second) - y.begin() + 1, 1, t);
}
return res;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr); cout.tie(nullptr);
cin >> n >> k;
vector<pair<int, int> > p(n);
vector<int> y;
for (int i = 0; i < n; ++i) {
int a, b; cin >> a >> b;
p[i].first = a + b;
p[i].second = a - b;
y.emplace_back(p[i].second);
}
sort(p.begin(), p.end());
sort(y.begin(), y.end());
y.erase(unique(y.begin(), y.end()), y.end());
int L = 0, R = 4e8, mid;
while (R > L) {
mid = (L + R) >> 1;
if (check(mid, p, y) < k) L = mid + 1;
else R = mid;
}
cout << L;
}
D. Lexicographically Minimal Shortest Path
题意:给定一个 \(n\) 个点 \(m\) 条边的无向无权图,每条边都有一个字母,要求找出该图中从节点 \(1\) 到节点 \(n\) 的字典序最小的最短路。
分析:我们先将所有点距离点 \(n\) 的距离预处理出来,由于无权边,因此一个 \(O(m)\) 的 \(BFS\) 就能解决。随后,从节点 \(1\) 出发,搜索所有后继节点,并找到所有后继节点中距离点 \(n\) 的距离为前驱节点到点 \(n\) 距离减一的节点中字典序最小的那个(如果有多个就全部丢进 \(vector\) ),然后重复这一操作直到找到字典序最小的最短路。
#include <bits/stdc++.h>
#define ll long long
#define mp make_pair
#define SIZE 200010
using namespace std;
vector<pair<int, char> > vec[SIZE];
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr); cout.tie(nullptr);
int n, m; cin >> n >> m;
for (int i = 0; i < m; ++i) {
int a, b; char c;
cin >> a >> b >> c;
--a, --b;
vec[a].emplace_back(mp(b, c));
vec[b].emplace_back(mp(a, c));
}
vector<int> dis(n, -1);
queue<int> q;
q.push(n - 1);
dis[n - 1] = 0;
while (!q.empty()) {
int top = q.front();
q.pop();
for (auto i : vec[top]) {
int to = i.first;
if (dis[to] == -1) {
dis[to] = dis[top] + 1;
q.push(to);
}
}
}
string ans = "";
vector<int> pa(n, -1);
vector<int> tmp;
tmp.emplace_back(0);
for (int i = 0; i < dis[0]; ++i) {
char minc = 'z' + 1;
vector<int> nxt;
for (auto j : tmp) {
for (auto k : vec[j]) {
if (dis[k.first] == dis[j] - 1) {
if (k.second < minc) {
pa[k.first] = j;
minc = k.second;
nxt = { k.first };
}
else if (k.second == minc) {
pa[k.first] = j;
nxt.emplace_back(k.first);
}
}
}
}
sort(nxt.begin(), nxt.end());
nxt.erase(unique(nxt.begin(), nxt.end()), nxt.end());
tmp = nxt;
ans += minc;
}
vector<int> path;
int fa = n - 1;
while (fa != -1) {
path.emplace_back(fa + 1);
fa = pa[fa];
}
reverse(path.begin(), path.end());
cout << path.size() - 1 << '\n';
for (auto i : path) cout << i << ' ';
cout << '\n' << ans;
}
E. Fluctuations of Mana
题意:略。
分析:前缀和求最值。
#include <bits/stdc++.h>
#define ll long long
using namespace std;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr); cout.tie(nullptr);
ll n, ans = 1e18;
cin >> n;
vector<ll> a(n);
vector<ll> pre(n);
for (auto& i : a) cin >> i;
for (int i = 0; i < n; ++i) pre[i] = (!i ? a[i] : a[i] + pre[i - 1]);
for (auto i : pre) ans = min(ans, i);
cout << (ans >= 0 ? 0 : -ans);
}
F. Moving Target
题意:有一排编号分别为 \(1,2,\cdots,n\) 的窗户,某个窗户后面有一个目标物,你每次可以打开一个窗户来寻找这个目标物,如果找到就结束了,如果没找到就要继续找并且该目标物会转移到右边的窗户(即从 \(k\) 变成 \(k+1\) ),请你给出一种寻找次数最少的构造,必须保证一定能够找到这个目标物。
分析:其实就是构造一个 1 3 5 ... 的数列,注意特判奇偶。
#include <bits/stdc++.h>
#define ll long long
using namespace std;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr); cout.tie(nullptr);
int n; cin >> n;
cout << ((n & 1) ? (n + 1) / 2 : n / 2 + 1);
cout << '\n';
for (int i = 0; i < (n + 1) / 2; ++i) cout << 2 * i + 1 << ' ';
if (!(n & 1)) cout << n;
}
G. Nuts and Bolts
题意:交互题。有 \(n\) 个尺寸为 \(1,2,\cdots,n\) 的螺栓和螺母,现在他们的顺序被打乱了,你需要将他们两两配对(大小相同的),最多能够询问 \(5n\log n\) 次。每次询问中,你可以询问两个下标 \(i\) 和 \(j\) 表示询问第 \(i\) 个螺栓和第 \(j\) 个螺母的大小关系,如果螺栓的尺寸大于螺母将返回 \(>\) ,若等于返回 \(=\) ,若小于返回 \(<\) 。
分析:肯定是分治的思想,我们每次随机一个下标 \(x\) ,通过两次 \(O(n)\) 的询问将数组 \(a\) 中小于 \(a[x]\) 的元素和大于 \(a[x]\) 的元素分别丢进两个数组,将数组 \(b\) 中小于 \(a[x]\) 的元素和大于 \(a[x]\) 的元素分别丢进两个数组,并且找到数组 \(b\) 中与 \(a[x]\) 相等的元素的下标。然后将小于 \(a[x]\) 的两个数组和大于 \(a[x]\) 的两个数组分成两组进行递归搜索,理论复杂度 \(O(n\log n)\) 。
#include <bits/stdc++.h>
#include <random>
using namespace std;
vector<int> ans;
void solve(vector<int>& A, vector<int>& B) {
if (A.empty()) return;
default_random_engine seed(time(0));
uniform_int_distribution<int> gen(0, A.size() - 1);
int x = A[gen(seed)];
int pos = -1;
vector<int> AL, AR, BL, BR;
for (auto i : B) {
cout << "? " << x + 1 << " " << i + 1 << endl;
char ch; cin >> ch;
if (ch == '<') BR.emplace_back(i);
else if (ch == '>') BL.emplace_back(i);
else pos = i;
}
ans[x + 1] = pos + 1;
for (auto i : A) {
cout << "? " << i + 1 << " " << pos + 1 << endl;
char ch; cin >> ch;
if (ch == '<') AL.emplace_back(i);
else if (ch == '>') AR.emplace_back(i);
}
solve(AL, BL);
solve(AR, BR);
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr); cout.tie(nullptr);
int n; cin >> n;
ans.resize(n + 1, -1);
vector<int> A(n), B(n);
for (int i = 0; i < n; ++i) A[i] = B[i] = i;
solve(A, B);
cout << "!";
for (int i = 1; i <= n; ++i) cout << " " << ans[i];
}
H. Tree Painting
题意:给定一棵 \(n\) 个点的树,现在每次操作能够选择树上的两个节点,然后将这两个节点之间的边和点全部染色,询问将整棵树的边和点完全染色需要几次操作。
分析:最优策略必定是每次选择两个叶子节点,然后将这两个节点间的路径染色,因此结果为 \(\frac{叶子节点数+1}{2}\) 。
#include <bits/stdc++.h>
#define ll long long
using namespace std;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr); cout.tie(nullptr);
int n; cin >> n;
vector<int> deg(n + 1);
for (int i = 1; i < n; ++i) {
int u, v; cin >> u >> v;
deg[u]++; deg[v]++;
}
int leaves = 0;
for (int i = 1; i <= n; ++i)
if (deg[i] == 1)
++leaves;
cout << (leaves + 1) / 2;
}
I. Sorting Colored Array
题意:给定一个数组,第 \(i\) 个位置的元素有一个数值 \(a_i\) 和一个颜色 \(c_i\) ,不同颜色的相邻元素可以交换位置,询问能否将数组交换为按照数值大小从小到大排列的。
分析:因为相同颜色的元素不能交换,因此我们将元素按照颜色分类存储,如果某种颜色的颜色中存在逆序对,那么就不能,否则就能。
#include <bits/stdc++.h>
#define SIZE 1000010
using namespace std;
bool check(vector<int>& a, vector<int>& b) {
for (int i = 0; i < a.size(); ++i)
if (a[i] != b[i])
return true;
return false;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr); cout.tie(nullptr);
int n; cin >> n;
map<int, vector<int> > MP;
for (int i = 1; i <= n; ++i) {
int x, y; cin >> x >> y;
MP[y].emplace_back(x);
}
for (auto it : MP) {
vector<int> a, b;
a = b = it.second;
sort(a.begin(), a.end());
if (check(a, b)) {
cout << "NO";
return 0;
}
}
cout << "YES";
}
J. The Battle of Mages
题意:输出答案题。有两个能随机召唤生物的法师,每个召唤出的生物有一个属性:攻击力。每个法师能从他的召唤池中召唤 \(k\) 只不同的生物,召唤出的生物攻击力之和更高的获胜。现在要求你构造出这两个法师的召唤池,使得 \(k=1,3\) 时,第一个法师胜率更高, \(k=2\) 时第二个法师胜率更高。
分析:略。
#include <bits/stdc++.h>
#define ll long long
using namespace std;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr); cout.tie(nullptr);
cout << "3\n2 7 7\n3\n5 5 5";
}
K. Table
题意:给定一个桌子的四个桌脚的长度,判断这四个桌脚能否恰好保证支撑起这个桌子(即保证桌面是一个平面)。
分析:如图:
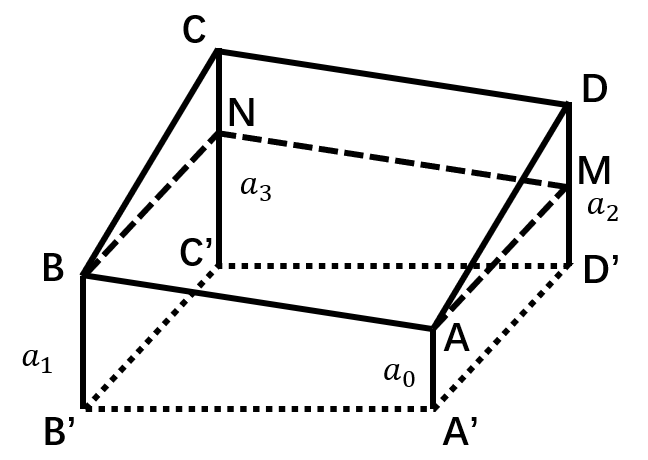
设这四根桌脚的长度分别为 \(a_0,a_1,a_2,a_3\) (从小到大排列),如果 \(ABCD\) 为一平面,则必须满足:
\(|DM|=|CN|\Leftrightarrow |CC'|=|CN|+|C'N|=|BB'|+|DM|\Leftrightarrow a_3=a_1+a_2-a_0\)
#include <bits/stdc++.h>
#define ll long long
using namespace std;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr); cout.tie(nullptr);
vector<int> a(4);
for (auto& i : a) cin >> i;
sort(a.begin(), a.end());
if (a[3] == a[2] + a[1] - a[0]) cout << "YES";
else cout << "NO";
}
L. The Dragon Land
题意:一个勇者需要穿越一片龙的领地,一共有 \(n\) 只龙,每只龙有一个赏金 \(a_i\) ,勇者每攻击一只龙都需要花钱修一次装备,第一次修花费 \(1\) ,每次修复的价格增加 \(1\) ,询问勇者最多能赚多少钱。
分析:排序一下贪心。
#include <bits/stdc++.h>
#define ll long long
using namespace std;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr); cout.tie(nullptr);
ll n; cin >> n;
vector<ll> a(n);
for (auto& i : a) cin >> i;
sort(a.begin(), a.end());
reverse(a.begin(), a.end());
ll ans = 0, cost = 1;
for (auto i : a) {
if (i > cost) {
ans += i - cost;
++cost;
}
}
cout << ans;
}
M. Notifications
题意:略。
分析:简单模拟。
#include <bits/stdc++.h>
#define ll long long
using namespace std;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr); cout.tie(nullptr);
int t; cin >> t;
vector<pair<ll, ll> > a(t);
for (auto& i : a) cin >> i.first >> i.second;
sort(a.begin(), a.end());
ll ans = a[0].first + a[0].second;
for (int i = 1; i < t; ++i) {
if (a[i].first <= ans) ans += a[i].second;
else ans = a[i].first + a[i].second;
}
cout << ans;
}


