2019-2020 ICPC Asia Hong Kong Regional Contest 部分题解
2019-2020 ICPC Asia Hong Kong Regional Contest
A. Axis of Symmetry
题意:给定一堆边和坐标轴平行且不重叠的矩形,找出所有对称轴。
分析:这题猜结论很简单,对称轴最多也就四条:两条垂直坐标轴的,两条对角线形式的(可以参考题面中样例的图片)。为了找出这四条对称轴,我们只需要找到整个图形的四条边界线。然后对所有的点进行 \(check\) ,检测是否每一个点都有关于对称轴对称的点。
这里对点的 \(check\) 有一个需要注意的点:被偶数个矩形覆盖的点不需要考虑,如下图(红色为偶数点,蓝色为奇数点):
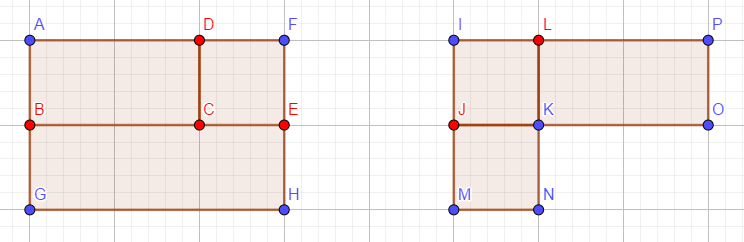
因为偶数点必定为 \(180°\) 或者 \(360°\) ,奇数点必定是 \(90°\) 或者 \(270°\) ,因此奇数点必定是转角,而偶数点则落在边上。算法实现用 \(map\) 存所有的点就行了,还需要注意输出格式要按字典序输出 !
#define _CRT_SECURE_NO_WARNINGS
#pragma GCC optimize(3)
#pragma GCC optimize("Ofast")
#pragma GCC target("sse,sse2,sse3,ssse3,sse4,popcnt,abm,mmx,avx,tune=native")
#pragma comment(linker, "/stack:200000000")
#include <bits/stdc++.h>
#define SIZE 5005
#define rep(i, a, b) for (int i = a; i <= b; ++i)
#define mp make_pair
#define ll long long
using namespace std;
void io() { ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr); }
int t, n;
bool vis[4];
vector<int> gao(int x, int y, int z) {
vector<int> ans(3);
int g = __gcd(x, __gcd(y, z));
if (x / g < 0) g = -g;
else if (x == 0 && y / g < 0) g = -g;
ans[0] = x / g; ans[1] = y / g; ans[2] = z / g;
return ans;
}
int main() {
io(); cin >> t;
while (t--) {
map<pair<int, int>, int> MP;
cin >> n;
rep(i, 0, 3) vis[i] = true;
int xa, ya, xb, yb;
int mxx = -2e9, mnx = 2e9, mxy = -2e9, mny = 2e9;
rep(i, 1, n) {
cin >> xa >> ya >> xb >> yb;
xa <<= 1; ya <<= 1; xb <<= 1; yb <<= 1;
MP[mp(xa, ya)] ^= 1;
MP[mp(xa, yb)] ^= 1;
MP[mp(xb, ya)] ^= 1;
MP[mp(xb, yb)] ^= 1;
mxx = max(mxx, xb);
mnx = min(mnx, xa);
mxy = max(mxy, yb);
mny = min(mny, ya);
}
int dx = (mxx + mnx) / 2, dy = (mxy + mny) / 2;
for (auto it : MP) {
if (!it.second) continue;
int x = it.first.first, y = it.first.second;
pair<int, int> pr = mp(x, dy - (y - dy));
vis[0] = (vis[0] && MP.count(pr) && MP[pr]);
pr = mp(dx - (x - dx), y);
vis[1] = (vis[1] && MP.count(pr) && MP[pr]);
pr = mp(dx + (y - dy), dy + (x - dx));
vis[2] = (vis[2] && MP.count(pr) && MP[pr]);
pr = mp(dx - (y - dy), dy - (x - dx));
vis[3] = (vis[3] && MP.count(pr) && MP[pr]);
}
vector<vector<int> > res;
if (vis[0]) res.emplace_back(gao(0, 2, dy));
if (vis[1]) res.emplace_back(gao(2, 0, dx));
if (vis[2]) res.emplace_back(gao(2, -2, dx - dy));
if (vis[3]) res.emplace_back(gao(2, 2, dx + dy));
sort(res.begin(), res.end(), [](auto& a, auto& b) {
if (a[0] != b[0]) return a[0] > b[0];
if (a[1] != b[1]) return a[1] > b[1];
return a[2] > b[2];
});
cout << res.size() << '\n';
for (auto it : res) cout << it[0] << ' ' << it[1] << ' ' << it[2] << ' ';
cout << '\n';
}
}
B. Binary Tree
题意:给定一棵树,两个人轮流进行游戏,一个人每次能从树上取走一棵符合满二叉树性质的子树,询问谁能必胜。
分析:满二叉树的节点数必定为奇数,因此决定胜负的是树上节点数的奇偶性。
#include <bits/stdc++.h>
using namespace std;
int main() {
int t; scanf("%d", &t);
while (t--) {
int n;
scanf("%d", &n);
int u, v;
for (int i = 1; i < n; i++)
scanf("%d%d", &u, &v);
if (n & 1) printf("Alice\n");
else printf("Bob\n");
}
}
C. Constructing Ranches
题意:给定一棵树,每个节点有一个权值 \(a_i\) ,询问树上有多少条路径满足:如果把这条路径经过的所有节点上的权值看作边长,那这些边可以构成一个简单多边形。
分析:边集 \(\{a_1,a_2,...,a_n\}\) 能构成简单多边形的充要条件是 \(\sum^n_{i=1}a_i>2\underset{1\leq j \leq n}{max}a_j\) ;就是边集中的最长边长度必须小于其余所有边长之和。
剩下的树分治队友写的。
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int maxn = 2e5 + 5;
const int maxm = 2e5 + 5;
int n;
LL ans, a[maxn];
struct Edge {
int v;
int next;
} edge[maxm << 1];
int head[maxn], tot;
void init(int n) {
fill(head, head + 1 + n, 0);
tot = 0;
}
inline void AddEdge(int u, int v) {
edge[++tot].v = v;
edge[tot].next = head[u];
head[u] = tot;
}
int n_size[maxn], dp[maxn], root, sum;
bool vis[maxn];
void GetRoot(int now, int fa) {
n_size[now] = 1;
dp[now] = 0;
for (int i = head[now]; i; i = edge[i].next) {
if (vis[edge[i].v] || edge[i].v == fa)
continue;
GetRoot(edge[i].v, now);
n_size[now] += n_size[edge[i].v];
dp[now] = max(dp[now], n_size[edge[i].v]);
}
dp[now] = max(dp[now], sum - n_size[now]);
if (dp[now] < dp[root])
root = now;
}
LL cal(int, LL);
void solve(int now) {
vis[now] = true;
ans += cal(now, 0);
for (int i = head[now]; i; i = edge[i].next) {
if (vis[edge[i].v])
continue;
ans -= cal(edge[i].v, a[now]);
root = 0;
dp[0] = sum = n_size[edge[i].v];
GetRoot(edge[i].v, 0);
solve(root);
}
}
void doit() {
memset(vis, 0, sizeof(vis));
dp[root = 0] = sum = n;
GetRoot(1, 0);
solve(root);
}
typedef pair<LL, LL> pll;
int cnt;
pll line[maxn], val[maxn];
void dfs_add(int now, LL maxval, LL w, int fa) {
cnt++;
line[cnt] = make_pair(w, cnt);
val[cnt].first = maxval;
for (int i = head[now]; i; i = edge[i].next) {
if (vis[edge[i].v] || edge[i].v == fa)
continue;
dfs_add(edge[i].v, max(maxval, a[edge[i].v]), w + a[edge[i].v], now);
}
}
int tree[maxn];
inline int lowbit(int x) { return x & -x; }
void update(int x, int val) {
for (int i = x; i <= cnt; i += lowbit(i))
tree[i] += val;
}
int query(int x) {
int res = 0;
for (int i = x; i; i -= lowbit(i))
res += tree[i];
return res;
}
LL cal(int now, LL w) {
cnt = 0;
dfs_add(now, max(w, a[now]), w + a[now], 0);
LL head = w ? w : val[1].first;
sort(line + 1, line + cnt + 1);
for (int i = 1; i <= cnt; i++)
val[line[i].second].second = i;
sort(val + 1, val + 1 + cnt);
fill(tree, tree + 1 + cnt, 0);
LL res = 0;
int left, right, mid;
LL limit, ret;
for (int i = 1; i <= cnt; i++) {
left = 1, right = cnt;
limit = 2 * val[i].first - line[val[i].second].first + head;
ret = 0;
while (left <= right) {
mid = (left + right) >> 1;
if (line[mid].first <= limit) {
ret = mid;
left = mid + 1;
} else right = mid - 1;
}
res += i - 1;
if (ret) res = res - query(ret);
update(val[i].second, 1);
}
return res;
}
int main() {
int t;
scanf("%d", &t);
while (t--) {
scanf("%d", &n);
for (int i = 1; i <= n; i++)
scanf("%lld", &a[i]);
init(n);
int u, v;
for (int i = 1; i < n; i++) {
scanf("%d%d", &u, &v);
AddEdge(u, v);
AddEdge(v, u);
}
ans = 0;
doit();
printf("%lld\n", ans);
}
}
D. Defining Labels
题意:进制转换。
#define _CRT_SECURE_NO_WARNINGS
#pragma GCC optimize(3)
#pragma GCC optimize("Ofast")
#pragma GCC target("sse,sse2,sse3,ssse3,sse4,popcnt,abm,mmx,avx,tune=native")
#pragma comment(linker, "/stack:200000000")
#include <bits/stdc++.h>
#define SIZE 200005
#define rep(i, a, b) for (int i = a; i <= b; ++i)
#define mp make_pair
#define ll long long
using namespace std;
void io() { ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr); }
int k, t, n;
void dfs(int x) {
if (x > k) dfs((x - 1) / k);
cout << 9 + (x % k == 0 ? k : x % k) - k;
}
int main() {
io(); cin >> t;
rep(i, 1, t) {
cin >> k >> n;
dfs(n);
cout << '\n';
}
}
E. Erasing Numbers
题意:给定一个 \(1,2,...,n\) 的排列 ( \(n\) 为奇数),你每次能从数组中选择连续的三个数,并删除这三个数中最大的和最小的(保留中位数),直到最后剩下一个数,询问该排列中的每一个数字能否成为最后剩下的数字。
分析:这题思路相当妙,首先观察数据范围,解法应该是遍历每一个数字,并 \(O(n)\) 判断这个数字能否留下;然后需要想到我们每次对某个数字 \(X\) 判断它能否留下来的关键在于最后一步时,它是否是最后三个数字的中位数。我们用 \(0\) 表示比 \(X\) 小的数,用 \(1\) 表示比 \(X\) 大的数,那么最后三个数必须是 \(01X\) 的一种排列。
接下来我们需要观察得到一个性质:当这个排列中的 \(0,1\) 数量相等时,数字 \(X\) 必定能够留下,因为 \(0,1\) 的数量相等,所以必定有 \(0,1\) 相邻的地方,我们对于这个相邻点进行一次消除,那么不论另外一个数字是什么,我们都能够保证恰好消除了一个 \(1\) ,一个 \(0\) ,于是最后剩下的只能是 \(01X\) 的一个排列。
因此我们将问题转化为:能否将排列中的 \(0,1\) 数量变得相等。要使 \(0,1\) 的数量变得相等,只有消除 \(111\) 或者 \(000\) 这样的情况,因此我们可以 \(O(n)\) 遍历并模拟这一过程。
再更新一个简单的正确性证明,已经理解了就不用管了:这道题最巧妙的地方其实是奇偶性,因为 \(n\) 是奇数,所以 \(0,1\) 的数量奇偶性一致,不论我们一次删除了两个相同数字还是不同数字,都不会改变 \(0,1\) 数量奇偶的一致性。再结合上面说明的性质,我们只需要让 \(0,1\) 的数量变成相等的就行了,如果无法变成相等的那么最后必然留下两个 \(0\) 或者 \(1\) 。
#define _CRT_SECURE_NO_WARNINGS
#pragma GCC optimize(3)
#pragma GCC optimize("Ofast")
#pragma GCC target("sse,sse2,sse3,ssse3,sse4,popcnt,abm,mmx,avx,tune=native")
#pragma comment(linker, "/stack:200000000")
#include <bits/stdc++.h>
#define SIZE 5005
#define rep(i, a, b) for (int i = a; i <= b; ++i)
#define mp make_pair
#define ll long long
using namespace std;
void io() { ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr); }
const int maxn = 2e5;
ll t, n, a[SIZE];
bool check(int pos) {
int dif = abs(a[pos] - (n + 1) / 2);
int f = (a[pos] < (n + 1) / 2);
int now = 0, num = 0;
rep(i, 1, n) {
if (i == pos) { now = 0; continue; }
int ff = (a[i] < a[pos]);
if (f == ff) now = max(now - 1, 0);
else {
++now;
if (now == 3) ++num, now -= 2;
}
}
return num >= dif;
}
int main() {
io(); cin >> t;
while (t--) {
cin >> n;
rep(i, 1, n) cin >> a[i];
rep(i, 1, n) {
if (check(i)) cout << 1;
else cout << 0;
}
cout << '\n';
}
}
G. Game Design
题意:构造一棵节点带权值的树。构造完成后,树上的每个叶子节点都会出现一个怪物,怪物会自底向上进攻根节点,现在你能够在任意个节点建造防御塔,防御塔的建造花费是你构造是给出的点权 \(c_i\) ,以建造防御塔后的节点为根的子树中的所有怪物都会被防御塔杀死。现在给定一个正整数 \(K\) 代表以最小花费修建防御塔拦截杀死怪物的不同方案数,要求给出这个构造。
分析:由于 \(K\) 的范围很大,我们肯定不能 \(O(K)\) 建树,因此需要递归建树。然后考虑构造的方案,如果当前节点的方案数为偶数,那么我们构造两个方案数分别为 \(2,\frac{n}{2}\) 的子节点;如果是奇数就构造两个方案数分别为 \(2,\frac{n}{2}\) 的子节点,并且根节点单独作为一种方案,递归终点是 \(k\leq 2\) 的时候,我们只需要建一条链即可。
#define _CRT_SECURE_NO_WARNINGS
#pragma GCC optimize(3)
#pragma GCC optimize("Ofast")
#pragma GCC target("sse,sse2,sse3,ssse3,sse4,popcnt,abm,mmx,avx,tune=native")
#pragma comment(linker, "/stack:200000000")
#include <bits/stdc++.h>
#define SIZE 200005
#define rep(i, a, b) for (int i = a; i <= b; ++i)
#define mp make_pair
#define ll long long
using namespace std;
void io() { ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr); }
int k, cnt;
int pa[SIZE], c[SIZE], tmp[SIZE];
int dfs(int k, int f) {
int now = ++cnt;
pa[now] = f;
if (k <= 2) {
pa[++cnt] = now;
c[cnt] = tmp[now] = 1;
c[now] = 3 - k;
return 1;
}
tmp[now] = dfs(k / 2, now) + dfs(2, now);
c[now] = tmp[now] + (k % 2 == 0);
return tmp[now];
}
int main() {
io(); cin >> k;
dfs(k, 0);
cout << cnt << '\n';
rep(i, 2, cnt) cout << pa[i] << ' ';
cout << '\n';
rep(i, 1, cnt) cout << c[i] << ' ';
}
I. Incoming Asteroids
队友写的强制在线数据结构?
#include<bits/stdc++.h>
#define ll long long
#define maxn 200010
#define mod 1000000007
using namespace std;
int goal[maxn], num[maxn], q[maxn][3], suc[maxn];
ll sum[maxn], pr[maxn][3];
struct cv {
ll x;
int num;
bool friend operator<(cv p, cv q) {
return p.x > q.x;
}
}hf;
priority_queue<cv>qu[maxn];
vector<int>ans;
void check(int x) {
if (suc[x]) return;
for (int i = 0; i < num[x]; i++) {
goal[x] -= sum[q[x][i]] - pr[x][i];
pr[x][i] = sum[q[x][i]];
}
if (goal[x] <= 0) {
suc[x] = 1;
ans.push_back(x);
return;
}
else {
hf.num = x;
for (int i = 0; i < num[x]; i++) {
hf.x = sum[q[x][i]] + (goal[x] + num[x] - 1) / num[x];
qu[q[x][i]].push(hf);
}
}
}
void add(int x) {
hf.num = x;
for (int i = 0; i < num[x]; i++) {
pr[x][i] = sum[q[x][i]];
hf.x = sum[q[x][i]] + (goal[x] + num[x] - 1) / num[x];
qu[q[x][i]].push(hf);
}
}
int main() {
int n, m, las = 0, cnt = 0;
scanf("%d%d", &n, &m);
while (m--) {
int fl;
scanf("%d", &fl);
if (fl == 1) {
cnt++;
scanf("%d%d", &goal[cnt], &num[cnt]);
goal[cnt] ^= las;
for (int i = 0; i < num[cnt]; i++) {
scanf("%d", &q[cnt][i]);
q[cnt][i] ^= las;
}
add(cnt);
}
else {
int x, y;
scanf("%d%d", &x, &y);
x ^= las, y ^= las;
las = 0;
sum[x] += y;
ans.clear();
while (!qu[x].empty()) {
cv tp = qu[x].top();
if (tp.x > sum[x]) break;
qu[x].pop();
check(tp.num);
}
sort(ans.begin(), ans.end());
las = ans.size();
printf("%d", las);
for (int i = 0; i < las; i++) printf(" %d", ans[i]);
printf("\n");
}
}
return 0;
}
J. Junior Mathematician
队友写的数位 \(dp\) 。
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int maxn = 5005;
const int maxm = 65;
const LL mod = 1e9 + 7;
int len, m, a[maxn], base[maxn];
LL dp[maxn][maxm][maxm];
LL dfs(int pos, int pre, int cut, bool limit) {
if (pos > len)
return cut == 0;
if (dp[pos][pre][cut] != -1 && (!limit))
return dp[pos][pre][cut];
LL res = 0;
int top = limit ? a[pos] : 9;
for (int i = 0; i <= top; i++) {
res += dfs(pos + 1, (pre + i) % m, (cut + i * (base[len - pos] - pre + m)) % m, i == top && limit);
if (res >= mod)
res -= mod;
}
if (!limit)
dp[pos][pre][cut] = res;
return res;
}
LL Part(char* s) {
int p = 1;
while (s[p] == '0')
p++;
len = strlen(s + p);
for (int i = 1; i <= len; i++)
a[i] = s[p + i - 1] - '0';
for (int i = 0; i <= len + 1; i++)
for (int j = 0; j <= m; j++)
for (int k = 0; k <= m; k++)
dp[i][j][k] = -1;
return dfs(1, 0, 0, true);
}
char l[maxn], r[maxn];
int main() {
int t;
scanf("%d", &t);
while (t--) {
scanf("%s%s", l + 1, r + 1);
scanf("%d", &m);
int len = strlen(l + 1);
for (int i = len; i >= 1; i--) {
if (l[i] >= '1') {
l[i]--;
break;
} else
l[i] = '9';
}
base[0] = 1;
for (int i = 1; i <= 5000; i++)
base[i] = LL(base[i - 1]) * 10 % m;
int ans = (Part(r) - Part(l) + mod) % mod;
printf("%d\n", ans);
}
return 0;
}


