树状数组学习笔记
树状数组学习笔记
树状数组
本文参考视频:https://www.bilibili.com/video/av69667943?from=search&seid=204489840113652018
lowbit 操作
int lowbit(int x) {
return x & (-x);
}
\(lowbit\) 操作是为了求出一个数字 \(x\) 在二进制形态下,最低位的 \(1\) 的大小。
例如 \((110100)_2\) 中最低位 \(1\) 的大小是 \((100)_2\) 。
\(lowbit\) 求解的方法是,先将 \(x\) 的二进制按位取反,然后 \(+1\) ,再按位与原数字。
例如:\((110100)_2\)
- 按位取反 \((001011)_2\)
- \(+1\) \((001100)_2\)
- 按位与原数 \((000100)_2\)
由于计算机中负数采用补码存储,于是第一、二步的操作可以简化为 \(\times (-1)\)
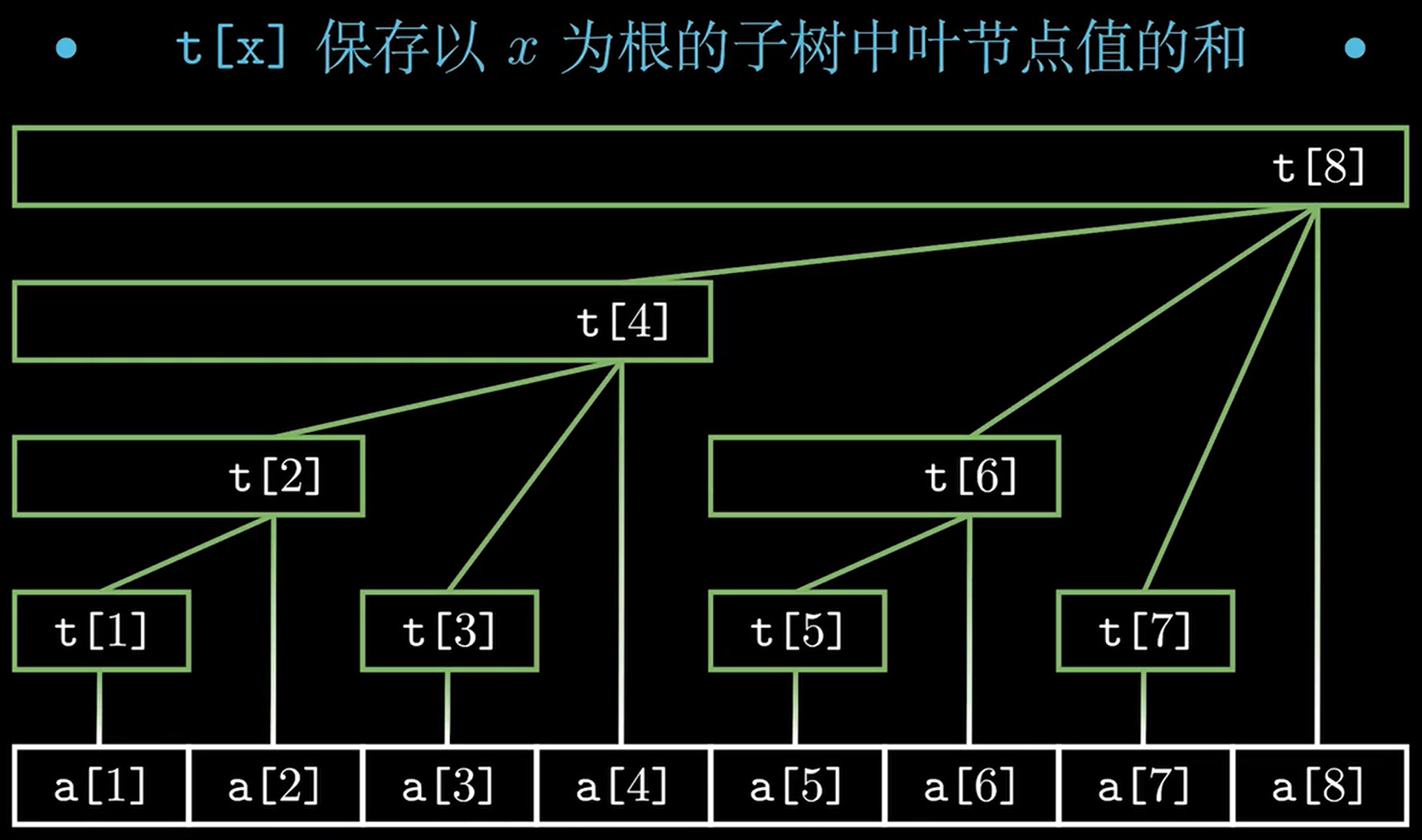
那么,\(lowbit\) 在树状数组中的作用到底是什么?实际上, \(lowbit(x)\) 代表树状数组中第 \(x\) 位元素覆盖的区间长度,(可以参考顶部图片)即 \(t[x] = \sum_{i=x-lowbit(x)+1}^xa[i]\)。(\(t[]\) 代表树状数组,\(a[]\) 代表原数组)
也就是说,树状数组中第 \(x\) 位元素的值代表当前位置到前 \(lowbit(x)\) 位置的所有原数组元素之和。
单点修改和区间查询
//以下代码,默认原数组为 a[],树状数组为 t[]
void add(int pos, int x) { //pos位置加上x
for (; pos <= n; pos += lowbit(pos)) { //n为数组大小
t[pos] += x;
}
}
int query_presum(int pos) { //查询pos位置的前缀和,即a1 + a2 + ... + apos
int ans = 0;
for (; pos > 0; pos -= lowbit(pos)) {
ans += t[pos];
}
return ans;
}
int query_sum(int l, int r) { //[l, r]区间查询
return query_presum(r) - query_presum(l - 1);
}
单点修改
树状数组中,每个节点 \(x\) 的父节点都可以表示为 \(x + lowbit(x)\) 。利用这个性质,我们就可以做到 \(O(logn)\) 单点修改。例如,我们想要给 \(a[3]+1\) ,那么我们需要对 \(t[3],t[4],t[8]\) \(+1\) 。
区间查询
区间查询我们需要利用前缀和,例如求 \([l, r]\) 的区间和,我们只需求 \(\sum_{i=1}^ra[i] - \sum_{i=1}^{l-1}a[i]\) 。利用 \(lowbit\) 的性质,我们知道 \(x\) 位置的元素覆盖的长度为 \(lowbit(x)\) 。于是我们只需每次将下标减去 \(lowbit(x)\) ,将当前位置的数值加上即可。例如 \(presum(7) = t[7] + t[6] + t[4]\) 。
例题1 P3374 【模板】树状数组 1
链接:https://www.luogu.com.cn/problem/P3374
#define _CRT_SECURE_NO_WARNINGS
#pragma GCC optimize(3)
#pragma GCC optimize("Ofast")
#pragma GCC target("sse,sse2,sse3,ssse3,sse4,popcnt,abm,mmx,avx,tune=native")
#pragma comment(linker, "/stack:200000000")
#include <bits/stdc++.h>
#define SIZE 500010
#define rep(i, a, b) for (long long i = a; i <= b; ++i)
#define ll long long
using namespace std;
void io() { ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr); }
int n, m;
int t[SIZE];
int lowbit(int x) { return x & (-x); }
void add(int pos, int x) { //pos位置加上x
for (; pos <= n; pos += lowbit(pos)) { //n为数组大小
t[pos] += x;
}
}
int query_presum(int pos) { //查询pos位置的前缀和,即a1 + a2 + ... + apos
int ans = 0;
for (; pos > 0; pos -= lowbit(pos)) {
ans += t[pos];
}
return ans;
}
int query_sum(int l, int r) { //[l, r]区间查询
return query_presum(r) - query_presum(l - 1);
}
int main() {
io(); cin >> n >> m;
rep(i, 1, n) {
int x; cin >> x;
add(i, x);
}
rep(i, 1, m) {
int op; cin >> op;
if (op == 1) {
int pos, x; cin >> pos >> x;
add(pos, x);
}
else {
int l, r; cin >> l >> r;
ll ans = query_sum(l, r);
cout << ans << '\n';
}
}
}
区间修改和单点查询
这一部分的建树与之前不同,先前所述的单点修改和区间查询,我们只需要对于 \(a[i]\) 建立树状数组;但是现在我们需要对 \(a[i]\) 的差分数组 \(p[i]\) 建树。
void add(int l, int r, int x) { //[l, r] 区间+x
add(l, x);
add(r + 1, -x);
}
int query_presum(int pos) { //单点查询,即对差分数组求前缀和
int ans = 0;
for (; pos > 0; pos -= lowbit(pos)) {
ans += t[pos];
}
return ans;
}
差分思想
为了快速实现区间加和单点查询操作,我们需要维护一个差分数组 \(p[i] = a[i] - a[i-1]\) ,然后对 \(p[i]\) 建树;我们容易发现,对于差分数组求前缀和,即为单点查询:
\(\sum_{i-1}^xp[i]=(a[x]-a[x-1]) + (a[x-1]-a[x-2]) + ... + (a[2]-a[1]) + a[1] = a[x]\)
于是,对于一个差分数组,我们可以利用树状数组 \(O(logn)\) 求前缀和的性质,实现更快的单点查询。那么,如何实现区间修改操作?
我们不难发现, \(a\) 数组的区间 \([l, r]\) 同时加上一个数值 \(x\) 时,它的差分数组只有首尾两项的值会发生变化,因为差分数组维护的是相邻数字的差值,所以一个区间同时加上一个数字时,这个区间中的相邻数字的差值其实不会改变。于是,我们只需要对 \(p[l]+x,p[r + 1-x]\) 即可,即进行两次单点修改。
例题2 P3368 【模板】树状数组 2
链接:https://www.luogu.com.cn/problem/P3368
#define _CRT_SECURE_NO_WARNINGS
#pragma GCC optimize(3)
#pragma GCC optimize("Ofast")
#pragma GCC target("sse,sse2,sse3,ssse3,sse4,popcnt,abm,mmx,avx,tune=native")
#pragma comment(linker, "/stack:200000000")
#include <bits/stdc++.h>
#define SIZE 500010
#define rep(i, a, b) for (long long i = a; i <= b; ++i)
#define ll long long
using namespace std;
void io() { ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr); }
int n, m;
int t[SIZE], a[SIZE];
int lowbit(int x) { return x & (-x); }
void add(int pos, int x) { //pos位置加上x
for (; pos <= n; pos += lowbit(pos)) { //n为数组大小
t[pos] += x;
}
}
void add(int l, int r, int x) { //[l, r] 区间+x
add(l, x);
add(r + 1, -x);
}
int query_presum(int pos) { //单点查询,即对差分数组求前缀和
int ans = 0;
for (; pos > 0; pos -= lowbit(pos)) {
ans += t[pos];
}
return ans;
}
int main() {
io(); cin >> n >> m;
rep(i, 1, n) cin >> a[i];
rep(i, 1, n) {
int x = a[i] - a[i - 1];
add(i, x);
}
rep(i, 1, m) {
int op; cin >> op;
if (op == 1) {
int l, r, x; cin >> l >> r >> x;
add(l, r, x);
}
else {
int pos; cin >> pos;
ll ans = query_presum(pos);
cout << ans << '\n';
}
}
}
区间修改和区间查询
对于单点修改,我们可以做到区间查询;那么,对于区间修改我们是否只能做到单点查询?答案是否定的,我们仍然可以通过维护差分数组的方法做到区间查询。
void add(int pos, int x, int t[]) { //因为要维护两个数组,加一个参数
for (; pos <= n; pos += lowbit(pos)) {
t[pos] += x;
}
}
void add(int l, int r, int x) { //[l, r] 区间+x
add(l, x, t1);
add(r + 1, -x, t1);
add(l, l * x, t2);
add(r + 1, -x * (r + 1), t2);
}
int query_presum(int pos, int t[]) { //单点查询,即对差分数组求前缀和
int ans = 0;
for (; pos > 0; pos -= lowbit(pos)) {
ans += t[pos];
}
return ans;
}
int query_sum2(int l, int r) { //区间修改下的区间查询
int p1 = l * query_presum(l - 1, t1) - query_presum(l - 1, t2);
int p2 = (r + 1) * query_presum(r, t1) - query_presum(r, t2);
return p2 - p1;
}
区间查询
我们仍然是从前缀和的角度出发,对于一个区间查询操作,我们看作两次前缀和查询。
因此我们考虑求 \(presum(x)=\sum^{x}_{i=1}a[i]=\sum^{x}_{i=1}\sum^{i}_{j=1}p[j]\) 。显然,这个式子难以计算,我们需要对它变形:
\(\sum^{x}_{i=1}\sum^{i}_{j=1}p[j]=(x+1)\sum_{i=1}^{x}p[i]-\sum_{i=1}^{x}i\times p[i]\) (这步变换通过几何意义更容易理解,可参考上文提到的视频)
对于上述变形,我们可以使用另一个树状数组维护 \(i\times p[i]\) 的前缀和来快速计算这个式子(想一想为什么?因为 \(p[i]\) 是一个差分数组,区间修改只会改变两项数值,因此 \(\times i\) 后,仍然只有首尾两项变化)。即:
//区间 [l, r] + x 操作时,还需要维护新的差分数组 i * p[i]
add1(l, x);
add1(r + 1, -x);
add2(l, l * x);
add2(r + 1, -x * (r + 1))
//add1操作维护 p[i],add2操作维护 i * p[i]
例题3 P3372 【模板】线段树 1
链接:https://www.luogu.com.cn/problem/P3372
#define _CRT_SECURE_NO_WARNINGS
#pragma GCC optimize(3)
#pragma GCC optimize("Ofast")
#pragma GCC target("sse,sse2,sse3,ssse3,sse4,popcnt,abm,mmx,avx,tune=native")
#pragma comment(linker, "/stack:200000000")
#include <bits/stdc++.h>
#define SIZE 500010
#define rep(i, a, b) for (long long i = a; i <= b; ++i)
#define int long long
using namespace std;
void io() { ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr); }
int n, m;
int t1[SIZE], t2[SIZE], a[SIZE];
int lowbit(int x) { return x & (-x); }
void add(int pos, int x, int t[]) { //因为要维护两个数组,加一个参数
for (; pos <= n; pos += lowbit(pos)) {
t[pos] += x;
}
}
void add(int l, int r, int x) { //[l, r] 区间+x
add(l, x, t1);
add(r + 1, -x, t1);
add(l, l * x, t2);
add(r + 1, -x * (r + 1), t2);
}
int query_presum(int pos, int t[]) { //单点查询,即对差分数组求前缀和
int ans = 0;
for (; pos > 0; pos -= lowbit(pos)) {
ans += t[pos];
}
return ans;
}
int query_sum2(int l, int r) { //区间修改下的区间查询
int p1 = l * query_presum(l - 1, t1) - query_presum(l - 1, t2);
int p2 = (r + 1) * query_presum(r, t1) - query_presum(r, t2);
return p2 - p1;
}
signed main() {
io(); cin >> n >> m;
rep(i, 1, n) cin >> a[i];
rep(i, 1, n) {
int x = a[i] - a[i - 1];
add(i, x, t1);
add(i, x * i, t2);
}
rep(i, 1, m) {
int op; cin >> op;
if (op == 1) {
int l, r, x; cin >> l >> r >> x;
add(l, r, x);
}
else {
int l, r; cin >> l >> r;
cout << query_sum2(l, r) << '\n';
}
}
}
简单应用
P1908 逆序对
链接:https://www.luogu.com.cn/problem/P1908
题解:求逆序对不仅可以归并排序,还能用树状数组解决。由于数据可能很大,所以我们需要先对数据离散化。离散化实际上就是建立原数组到一个 \(1,2,3, ..., n\) 的数组的映射关系;例如 24 33 1 99 25 等价于 2 4 1 5 3。
需要注意的是,原数组中如果有相等的元素,离散化后他们的相对位置不能变化
完成离散化后,我们考虑如何对离散化数组求逆序对:对于任意一个位置 \(pos\) 的元素而言,我们需要求的实际上就是在 \(a_{pos}\) 之前并且大于它的元素,联系到树状数组能够快速维护前缀和的性质,我们不难发现我们只需要把某一位置之前所有小于它的元素置为 \(1\) ,小于它的元素置为 \(0\) ,就能用前缀和快速计算贡献。
设离散化后的数组为 \(p[]\) ,对于这个数组我们从 \(1\) 到 \(n\) 遍历,在任意一个位置 \(j\) 做如下操作:
for (int j = 1; j <= n; ++j) {
add(j, 1); //单点修改,将 p[j] 置为 1
ans += j - presum(p[j]); //计算贡献
}
显然,对于 \(p_j\) 而言,要统计他的贡献不需要考虑 \(j\) 位置之后的元素,上方所述的操作就可以将所有逆序对找到。
#define _CRT_SECURE_NO_WARNINGS
#pragma GCC optimize(3)
#pragma GCC optimize("Ofast")
#pragma GCC target("sse,sse2,sse3,ssse3,sse4,popcnt,abm,mmx,avx,tune=native")
#pragma comment(linker, "/stack:200000000")
#include <bits/stdc++.h>
#define SIZE 500010
#define rep(i, a, b) for (long long i = a; i <= b; ++i)
#define int long long
using namespace std;
void io() { ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr); }
int n, m, ans;
int t[SIZE], a[SIZE];
int pos[SIZE]; //离散化
struct Node {
int val;
int id;
bool operator< (const Node& b) {
return (val < b.val) || (val == b.val && id < b.id);
}
}p[SIZE];
int lowbit(int x) { return x & (-x); }
void add(int pos, int x) {
for (; pos <= n; pos += lowbit(pos)) {
t[pos] += x;
}
}
int query_presum(int pos) {
int ans = 0;
for (; pos > 0; pos -= lowbit(pos)) {
ans += t[pos];
}
return ans;
}
signed main() {
io(); cin >> n;
rep(i, 1, n) cin >> p[i].val, p[i].id = i;
sort(p + 1, p + 1 + n);
rep(i, 1, n) pos[p[i].id] = i;
rep(i, 1, n) {
add(pos[i], 1);
ans += i - query_presum(pos[i]);
}
cout << ans;
}
P1972 [SDOI2009]HH的项链
链接:https://www.luogu.com.cn/problem/P1972
题解:刚开始想这道题的时候可能会认为需要一些可持久化的数据结构维护,事实上我们只需要通过树状数组维护即可。
首先,我们先要想到可以通过离线操作使得无序给出的查询区间有序,使得我们可以避免重复更新区间。先将所有区间读入,然后以区间右端点为关键字排序。然后我们维护一个树状数组,来记录贝壳的种类数量;但是某个贝壳重复出现怎么办?事实上对于重复出现的贝壳,我们只需要考虑最右边的贝壳:例如 1 2 3 1 2 ,实际上是 0 0 1 1 1 。更新过程如下:(自上而下对应 \(5\) 次更新)
1 0 0 0 0
1 1 0 0 0
1 1 1 0 0
0 1 1 1 0
0 0 1 1 1
为了实现这个过程,我们还需要一个数组来记录某种贝壳是否先前出现过,以及它出现的位置。于是,我们就可以对于每个询问区间更新到它的右端点,并且只保留最后出现的贝壳。这样,对于每次询问的区间 \([l,r]\) ,我们只需要记录 \(query\)_\(sum(l,r)\) 即可
#define _CRT_SECURE_NO_WARNINGS
#pragma GCC optimize(3)
#pragma GCC optimize("Ofast")
#pragma GCC target("sse,sse2,sse3,ssse3,sse4,popcnt,abm,mmx,avx,tune=native")
#pragma comment(linker, "/stack:200000000")
#include <bits/stdc++.h>
#define SIZE 500010
#define rep(i, a, b) for (long long i = a; i <= b; ++i)
#define int long long
using namespace std;
void io() { ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr); }
int n, m, k, ans, nxt;
int t[SIZE], a[SIZE];
int Map[SIZE];
int lowbit(int x) { return x & (-x); }
struct Node {
int l, r;
int id;
bool operator< (const Node& b) {
return (r < b.r) || (r == b.r && l < b.l);
}
}p[SIZE];
void add(int pos, int x) {
for (; pos <= n; pos += lowbit(pos)) {
t[pos] += x;
}
}
int query_presum(int pos) {
int ans = 0;
for (; pos > 0; pos -= lowbit(pos)) {
ans += t[pos];
}
return ans;
}
int query_sum(int l, int r) {
return query_presum(r) - query_presum(l - 1);
}
signed main() {
io(); cin >> n;
rep(i, 1, n) cin >> a[i];
cin >> m;
rep(i, 1, m) cin >> p[i].l >> p[i].r, p[i].id = i;
sort(p + 1, p + 1 + m);
nxt = 1;
vector<int> vec(m + 1);
rep(i, 1, m) {
rep(j, nxt, p[i].r) {
if (Map[a[j]]) add(Map[a[j]], -1);
add(j, 1);
Map[a[j]] = j;
}
nxt = p[i].r + 1;
vec[p[i].id] = query_sum(p[i].l, p[i].r);
}
rep(i, 1, m) cout << vec[i] << '\n';
}
P5673 【SWTR-02】Picking Gifts
链接:https://www.luogu.com.cn/problem/P5673
题解:显然,本题可以看作是前一题的升级版。不同点在于,上一题一个区间内不能存在相同元素;而这一题可以从右往左存在 \(k\) 个相同元素,处理方法和前一题类似。
#define _CRT_SECURE_NO_WARNINGS
#pragma GCC optimize(3)
#pragma GCC optimize("Ofast")
#pragma GCC target("sse,sse2,sse3,ssse3,sse4,popcnt,abm,mmx,avx,tune=native")
#pragma comment(linker, "/stack:200000000")
#include <bits/stdc++.h>
#define SIZE 500010
#define rep(i, a, b) for (long long i = a; i <= b; ++i)
#define int long long
using namespace std;
void io() { ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr); }
int n, m, k, ans, nxt;
int t[SIZE], a[SIZE], v[SIZE];
vector<int> q[SIZE];
vector<int> vec(SIZE >> 1);
int lowbit(int x) { return x & (-x); }
struct Node {
int l, r;
int id;
bool operator< (const Node& b) {
return (r < b.r) || (r == b.r && l < b.l);
}
}p[SIZE];
void add(int pos, int x) {
for (; pos <= n; pos += lowbit(pos)) {
t[pos] += x;
}
}
int query_presum(int pos) {
int ans = 0;
for (; pos > 0; pos -= lowbit(pos)) {
ans += t[pos];
}
return ans;
}
int query_sum(int l, int r) {
return query_presum(r) - query_presum(l - 1);
}
int main() {
io(); cin >> n >> m >> k; --k;
rep(i, 1, n) cin >> a[i];
rep(i, 1, n) cin >> v[i], add(i, v[i]);
rep(i, 1, m) {
cin >> p[i].l >> p[i].r;
p[i].id = i;
}
sort(p + 1, p + 1 + m);
nxt = 1;
rep(i, 1, m) {
rep(j, nxt, p[i].r) {
if (q[a[j]].size() >= k) {
add(q[a[j]][0], -v[q[a[j]][0]]);
q[a[j]].erase(q[a[j]].begin());
}
q[a[j]].emplace_back(j);
}
nxt = p[i].r + 1;
vec[p[i].id] = query_sum(p[i].l, p[i].r);
}
rep(i, 1, m) cout << vec[i] << '\n';
}
P3369 【模板】普通平衡树
链接:https://www.luogu.com.cn/problem/P3369
题解:首先肯定要离线操作,然后离散化,注意操作 \(4\) 不需要离散化。
单点加减操作我们已经很熟悉了,只需要分别对于元素所在位置 \(+1\) 和 \(-1\) 即可。
接着就是本题的核心操作求元素排名,第 \(k\) 大元素和前驱后继。为了方便表述,我们将离散化后的数组表示为 \(a[]\) 。
那么求元素 \(a[pos]\) 的排名就变得相当简单了,注意到增删元素只是 \(±1\) ,因此 \(a[pos]\) 的排名即为 \(query\)_\(presum(a[pos] - 1) + 1\) ,即求出所有比它小的元素数量然后 \(+1\) 。可以注意的一点是,求逆序对的操作就是求排名。
对于第 \(k\) 大元素,注意到树状数组的二进制特征,我们可以使用倍增快速找到其位置(不熟悉倍增思想可以回想一下快速幂的实现。由于树状数组的 \(lowbit\) 构成特征,我们可以通过倍增优化算法而不是二分查找)。具体实现可以参考代码中的 \(kth()\) 函数,并且结合树状数组的构成图理解。
有了上面的两种思想,我们不难发现求前驱和后继就是上述操作的综合,先求出元素 \(a[pos]\) 的排名 \(rank_{a[pos]}\) ,前驱和后继就能分别表示为第 \(rank_{a[pos]}-1\) 和 \(rank_{a[pos]} + 1\) 大元素。
#define _CRT_SECURE_NO_WARNINGS
#pragma GCC optimize(3)
#pragma GCC optimize("Ofast")
#pragma GCC target("sse,sse2,sse3,ssse3,sse4,popcnt,abm,mmx,avx,tune=native")
#pragma comment(linker, "/stack:200000000")
#include <bits/stdc++.h>
#define SIZE 500010
#define rep(i, a, b) for (long long i = a; i <= b; ++i)
#define int long long
using namespace std;
void io() { ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr); }
int n, m, k, ans, cnt;
int t[SIZE], op[SIZE], a[SIZE], p[SIZE];
int lowbit(int x) { return x & (-x); }
void add(int pos, int x) {
for (; pos <= n; pos += lowbit(pos)) {
t[pos] += x;
}
}
int query_presum(int pos) {
int ans = 0;
for (; pos > 0; pos -= lowbit(pos)) {
ans += t[pos];
}
return ans;
}
int query_sum(int l, int r) {
return query_presum(r) - query_presum(l - 1);
}
int kth(int k) {
int ans = 0, cnt = 0;
for (int i = 20; i >= 0; i--) {
ans += (1 << i);
if (ans > n || cnt + t[ans] >= k) ans -= (1 << i);
else cnt += t[ans];
}
return ++ans;
}
int main() {
io(); cin >> n;
rep(i, 1, n) {
cin >> op[i] >> a[i];
if (op[i] != 4) p[++cnt] = a[i];
}
sort(p + 1, p + 1 + cnt);
rep(i, 1, n) { //离散化
if (op[i] != 4) {
a[i] = lower_bound(p + 1, p + 1 + cnt, a[i]) - p;
}
}
rep(i, 1, n) {
if (op[i] == 1) add(a[i], 1);
else if (op[i] == 2) add(a[i], -1);
else if (op[i] == 3) cout << query_presum(a[i] - 1) + 1 << '\n';
else if (op[i] == 4) cout << p[kth(a[i])] << '\n';
else if (op[i] == 5) cout << p[kth(query_presum(a[i] - 1))] << '\n';
else cout << p[kth(query_presum(a[i]) + 1)] << '\n';
}
}
由于硬盘损坏,许多数据丢失,保留的笔记先挂到博客上。


