UVA - 13024 Saint John Festival 凸包+二分
题目链接:https://vjudge.net/problem/UVA-13024
题意:先给出\(L\)个点构造一个凸包,再给出\(S\)个点,询问有几个点在凸包内。
题解:判断点是否在凸包内的模板题。最暴力的想法是\(o(n^2)\)枚举每个点,但实际上我们可以使用二分优化。具体操作就是以凸包最左侧点为起点,对每个点按斜率排序,然后把凸包分割成数个三角形,在这些三角形中二分查找斜率。复杂度便优化为\(o(nlogn)\)如下图。
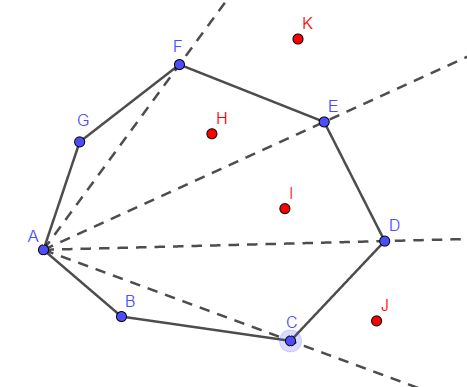
- 在凸包\(ABCDEFG\)中可二分查找\(H\),\(I\),\(J\),\(K\)点
完成二分后,通过叉积判断点是否在凸包内,如下图。

- \(\vec{FH}\times{\vec {HE}} < 0\),\(\vec{FK}\times{\vec {KE}} > 0\)
即叉积<0则在凸包内,>0在凸包外,同时还有叉积=0的情况(点在凸包的边上)。但是叉积=0时还应考虑一种情况,即在凸包一条边的延长线上,需要特判。如下图。
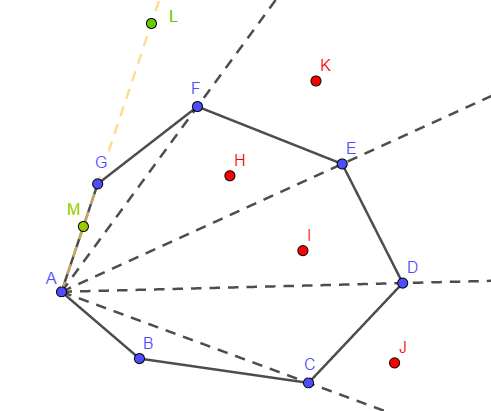
- 如图所示的\(L\)点和\(M\)点叉积均为0。
AC代码:
#include <bits/stdc++.h>
#define SIZE 100007
#define rep(i, a, b) for(int i = a; i <= b; ++i)
using namespace std;
typedef long long ll;
void io() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
}
ll n, m, t, num;
struct Point {
ll x, y;
double k;
friend bool operator<(const Point& a, const Point& b) { //为使用lower_bound进行运算符重载
return a.k <= b.k;
}
};
Point p[SIZE], ch[SIZE], tp[SIZE];
bool cmp(Point a, Point b) { //andrew算法排序预处理函数
if (a.x == b.x) return a.y < b.y;
else return a.x < b.x;
}
ll cross(Point a, Point b, Point c) { return (b.x - a.x) * (c.y - a.y) - (b.y - a.y) * (c.x - a.x); }
ll crossx(Point a, Point b, Point c) { return (a.x - b.x) * (c.y - a.y) - (a.y - b.y) * (c.x - a.x); }
ll andrew() { //采用安德鲁算法求凸包,返回顶点数
sort(p + 1, p + n + 1, cmp);
ll top = 0;
for (int i = 1; i <= n; ++i) {
while ((top > 1) && (cross(ch[top - 1], ch[top], p[i]) <= 0)) --top;
ch[++top] = p[i];
}
ll tmp = top;
for (int i = n - 1; i; --i) {
while ((top > tmp) && (cross(ch[top - 1], ch[top], p[i]) <= 0)) --top;
ch[++top] = p[i];
}
if (n > 1) top--;
return top;
}
bool InConvexHull(ll top, Point x) { //判断点x是否在凸包内
ll pos = lower_bound(ch + 1, ch + top + 1, x) - ch - 1; //二分查找
if (pos == 1) return false;
ll j = crossx(x, ch[pos], ch[pos + 1]);
if (j < 0) return true;
else if (j == 0) { //叉积为0时特判
ll minx = min(ch[pos].x, ch[pos + 1].x), maxx = max(ch[pos].x, ch[pos + 1].x);
ll miny = min(ch[pos].y, ch[pos + 1].y), maxy = max(ch[pos].y, ch[pos + 1].y);
if ((minx <= x.x) && (maxx >= x.x) && (miny <= x.y) && (maxy >= x.y)) return true;
else return false;
}
else return false;
}
int main() {
io();
while (cin >> n && n) { //多组输入
num = 0;
rep(i, 1, n) cin >> p[i].x >> p[i].y;
cin >> m;
ll top = andrew();
ll x = ch[1].x, y = ch[1].y;
rep(i, 2, top) { //计算斜率
double tx = ch[i].x - x, ty = ch[i].y - y;
if (!tx) { //若x坐标相同,则斜率设为1e18
if (ty < 0) ch[i].k = -1e18;
else ch[i].k = 1e18;
}
else ch[i].k = 1.0 * ty / tx;
}
ch[1].k = -1e18;
rep(i, 1, m) {
cin >> tp[i].x >> tp[i].y;
if (ch[1].x > tp[i].x) continue;
ll tx = tp[i].x - x, ty = tp[i].y - y;
Point x;
if (!tx) {
if (ty < 0) x.k = -1e18;
else x.k = 1e18;
}
else x.k = 1.0 * ty / tx;
x.x = tp[i].x, x.y = tp[i].y;
if (InConvexHull(top, x)) ++num; //计数
}
cout << num << endl;
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号