Codeforces Round #684 (Div. 2)E. Greedy Shopping（线段树区间最大值，最小值，区间和）

 

 

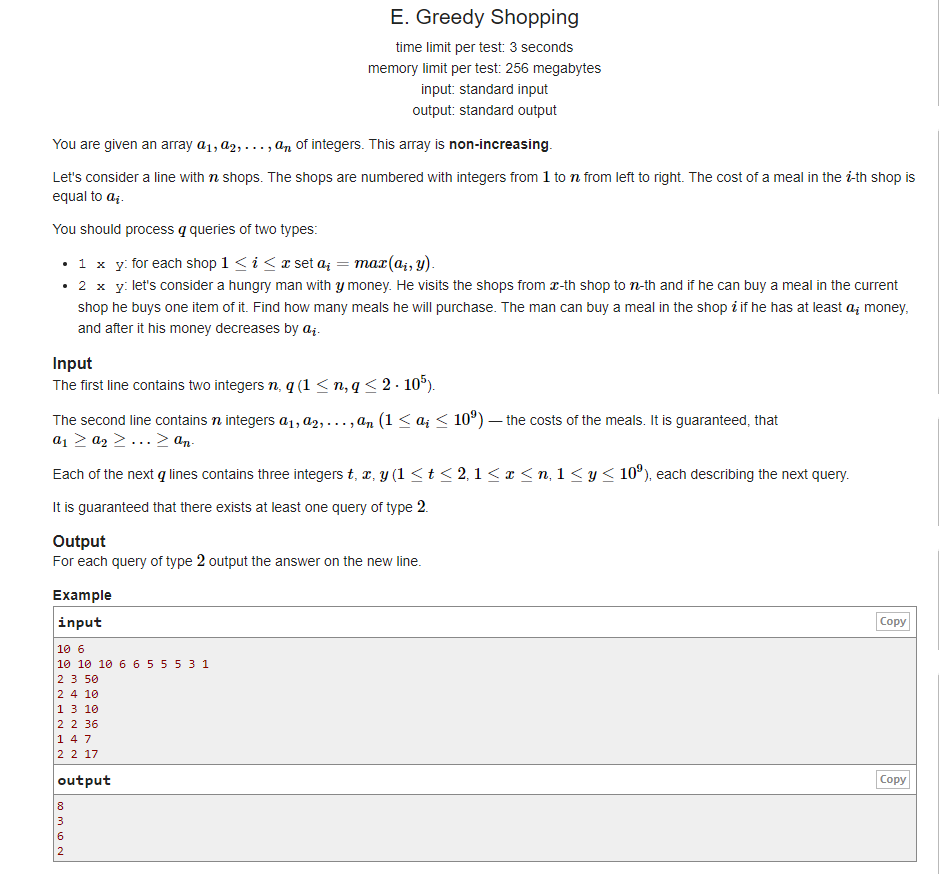
        题意：给出一个非严格递减的子序列，需要完成 m 次操作，分为下列两种类型：

     1>  1 x y：将区间 [ 1 , x ] 中的数进行 a[ i ] = max( a[ i ] , y ) 操作

     2>  2 x y：给出一个权值 y，从 x 开始往 n 走，遇到 a[ i ] 如果满足 a[ i ] <= y，购买该商品，问可以多少商品

思路：对于1操作我们可以维护一个区间最大值，如果当前值大于区间最大值，我们就把改区间修改掉。

          对于2操作，我么维护一个区间最小值，和区间和，如果当前的 y 小于区间的最小值，返回 0。如果当前的 y 大于当前区间的和，表示可以购买该区间所有的

         的商品，然后返回该区间的长度就可以了。

 

#include <iostream>
#include <string.h>
#include <string>
#include<cstdio>
#include <algorithm>
#define ll long long
using namespace std;
const int N=2e5+10;
int a[N];
int cnt;
ll ans;
struct node
{
    ll l,r;   // 左右区间的端点
    ll Mi,Mx,lazy;  //区间最大，最小，懒惰标记
    ll sum,len;   //区间和，该节点对应的区间长度。
} tree[N<<2];
void pushup(int n)
{
    tree[n].Mx=max(tree[n<<1].Mx,tree[n<<1|1].Mx);
    tree[n].Mi=min(tree[n<<1].Mi,tree[n<<1|1].Mi);
    tree[n].sum=tree[n<<1].sum+tree[n<<1|1].sum;
}
void pushdown(int n){
    if(tree[n].lazy){
        int val=tree[n].lazy;
        tree[n<<1].Mi=tree[n<<1].Mx=tree[n<<1].lazy=val;
        tree[n<<1|1].Mi=tree[n<<1|1].Mx=tree[n<<1|1].lazy=val;
        tree[n<<1].sum=tree[n<<1].len*val;
        tree[n<<1|1].sum=tree[n<<1|1].len*val;
        tree[n].lazy=0;
    }
}
void build_tree(int n,int l,int r){
    tree[n].l=l;
    tree[n].r=r;
    tree[n].lazy=0;
    tree[n].len=r-l+1;
    if(l==r) tree[n].Mi=tree[n].Mx=tree[n].sum=a[l];
    else{
        ll mid=(l+r)/2;
        int left_node= 2*n;
        int right_node=2*n+1;
        build_tree(left_node,l,mid);
        build_tree(right_node,mid+1,r);
        pushup(n);
    }
}
void update_tree(int n,int l,int r,int val )
{
    if(tree[n].Mi>=val) return ;
    if(tree[n].l>=l&&tree[n].r<=r&&tree[n].Mx<val){
        tree[n].sum=(tree[n].len)*val;
        tree[n].Mi=tree[n].Mx=tree[n].lazy=val;
        return ;
    }
    /*如果当前区间的最大值比我要更改的值要小，那么就把该区间修改掉。*/
    pushdown(n);   //向下更新。
    ll mid=(tree[n].l+tree[n].r)/2;
    if(l<=mid)  update_tree(n<<1,l,r,val);
    if(r>mid)   update_tree(n<<1|1,l,r,val);
    pushup(n);
}
int query_tree(int n,int l,int r)
{
    if(tree[n].Mi>cnt)   //很重要的一个减枝，不然递归会爆内存。
        return 0 ;
    if(tree[n].sum<=cnt&&tree[n].l>=l&&tree[n].r<=r){
        cnt-=tree[n].sum;
        return tree[n].len;
    }
     /*如果当前剩余的钱，可以购买该区间所有的商品，就把该区间所有的商品都买了*/
    pushdown(n);
    ll mid=(tree[n].l+tree[n].r)/2;
    int tp=0;
    if(l<=mid) tp+=query_tree(n<<1,l,r);
    if(r>mid)  tp+=query_tree(n<<1|1,l,r);
    return tp;
}
int main()
{
    int n,m;
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
        cin>>a[i];
    build_tree(1,1,n);
    while(m--){
        int op,x,y;
        scanf("%d%d%d",&op,&x,&y);
        if(op==1)
             update_tree( 1, 1, x, y );
        else
            cnt=y, printf("%d\n",query_tree( 1, x, n));
    }
}