最短路计数

 

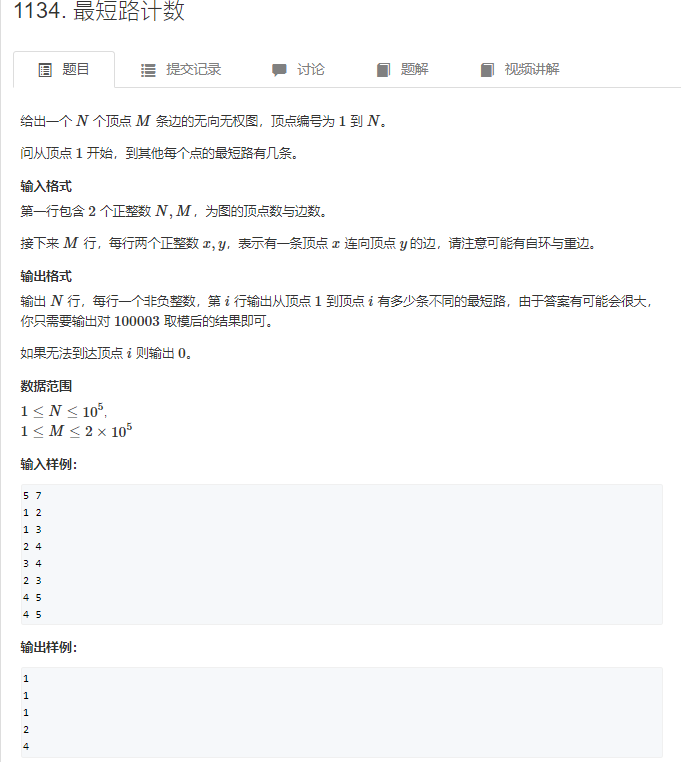
 题意：统计从1号点到所有的点的最短路的条数。

思路：权重都是1，开一个数组cnt [ N ], cnt[ i ]代表到 i 的最短路的个数。

如果dis[ v ]  >  dis[ u ] + 1,那么到 v 的最短路的个数也就是到 u 的个数( cnt [ v ]=cnt[ u ])。

 dis[ v ]  =  dis[ u ] + 1，那么到 v 的最短路的个数也就是到 u 的最短路个数+已经统计上的 到 v 的最短路的个数 (cnt[ v ]=cnt[ v ]+cnt[ u ] )。

#include <iostream>
#include <algorithm>
#include <queue>
#include <cstdio>
#include <cstring>
#include <vector>
using namespace std;
typedef long long ll;
#define pb push_back
const int N = 1e5+10;
int INF = 1e9+10;
const int mod=100003;
struct node
{
    int now, dis;
     friend bool operator<(node n1, node n2) //重载运算
    {
        return n1.dis> n2.dis;
    }
};
priority_queue<node>que;
struct Info{
    int to, dis;
};
vector<Info> E[N];
int dis[N], cost[N];
int cnt[N];
int vis[N];
int n, m;
void dijkstra(){
    for(int i = 0; i <= n; ++i){
        dis[i] = INF;
        cost[i] = INF;
        vis[i] = 0;
    }
    dis[1]=0;
    cnt[1]=1;
    que.push({1, dis[1]});
    while(!que.empty()){
        int now = que.top().now;   //当前到达的最短的那个点。
          que.pop();
        if(vis[now]==1)
        continue;
        vis[now]=1;
        int _size = E[now].size();
        for(int i = 0; i < _size; ++i){
            Info info = E[now][i];  //取出和now相连的点。
            if(dis[info.to] > dis[now] + 1)     //info.d  to和now的距离. dis[now] 从起点到now点的距离. dis[info.to] 从起点到info.to点的距离
            {
                dis[info.to] = dis[now] + 1;
                cnt[info.to]=cnt[now];
                que.push({info.to,dis[info.to]});
            }
            else if(dis[info.to] == dis[now] + 1){
                cnt[info.to]=(cnt[now]+cnt[info.to])%mod;
            }
        }
    }
}
void solve()
{

        scanf("%d%d", &n, &m);
        for(int i = 1; i <= m; i++){
            int u, v, d, w;
            scanf("%d%d", &u, &v);
            E[u].pb({v,w});
            E[v].pb({u,w});
        }
        dijkstra();
        for(int i=1;i<=n;i++)
            cout<<cnt[i]%mod<<endl;
        for(int i = 0; i < n; ++i){
            E[i].clear();
           cnt[i]=0;
        }
        while(!que.empty())
            que.pop();
}
int main()
{
    solve();
    return 0;
}