数据结构（七）排序---冒泡排序

冒泡排序是最容易想到的代码，也是最易写出的代码。但是当我学完这一节，发现我原来的冒泡排序写法，居然是伪冒泡....尴尬了

定义

冒泡排序（Bubble Sort）一种交换排序，他的基本思想是：两两比较相邻记录的关键字，如果反序则交换，知道没有反序的记录为止

数据：

int a[10] = { 5, 2, 6, 0, 3, 9, 1, 7, 4, 8 };

版本一---冒泡排序（我们最常想到的）

void BubbleSort01(SqList *L)
{
    int i, j;
    for (i = 1; i < L->length;i++)
    {
        for (j = i + 1; j <= L->length;j++)
        {
            if (L->r[i]>L->r[j])
                swap(L, i, j);    //交换顺序
        }
    }
}

严格来说，不是标准的冒泡排序，因为不满足“两两比较相邻记录”的冒泡排序思想。是使用第一个数据，从头比较到尾；然后选用第二个，以此类推，直到比较结束

int main()
{
    SqList s;
    s.length = 0;
    int i;
    int a[10] = { 5, 2, 6, 0, 3, 9, 1, 7, 4, 8 };
    for (i = 0; i < 10; i++)
    {
        s.r[i + 1] = a[i];
        s.length++;
    }

    BubbleSort01(&s);

    for (i = 1; i <= s.length; i++)
        printf("%d ", s.r[i]);

    system("pause");
    return 0;
}

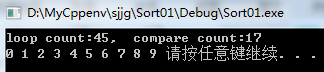
版本二---正宗冒泡排序

void BubbleSort02(SqList *L)
{
    int i, j, count1, count2;
    count1 = count2 = 0;
    for (i = 1; i < L->length; i++)
    {
        for (j = L->length-1; j >= i; j--)    //注意j是从后向前循环
        {
            count1++;
            if (L->r[j]>L->r[j+1])    //若前者大于后者
            {
                swap(L, j, j+1);    //交换顺序
                count2++;
            }
        }
    }
    printf("loop count:%d,  compare count:%d\n", count1, count2);
}

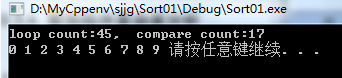
版本三：正宗冒泡排序优化（减少了循环次数）

冒泡排序会在某次比较后达到有序，此时我们就没有必要再去进行for循环比较了。我们可以设置一个标志位，若是在某次循环中没有发生序列变化，就代表了已经排序完成，我们不需要后面的排序了。

void BubbleSort03(SqList *L)
{
    int i, j, count1, count2, flag;
    count1 = count2 = 0;
    flag = 1;
    for (i = 1; i < L->length&&flag; i++)
    {
        flag = 0;
        for (j = L->length - 1; j >= i; j--)    //注意j是从后向前循环
        {
            count1++;
            if (L->r[j]>L->r[j + 1])    //若前者大于后者
            {
                swap(L, j, j + 1);    //交换顺序
                count2++;
                flag = 1;
            }
        }
//         if (flag == 0)    //上次排序中没有发生序列变化，说明已经完成排序
//             break;    
    }
    printf("loop count:%d,  compare count:%d\n", count1, count2);
}

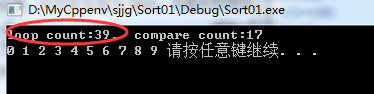
时间复杂度

最坏时间复杂度为O(n*(n-1)/2)--->O(n^2)