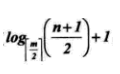数据结构（六）查找---多路查找树（B树）

B 树

B树与B+树

一：定义

B树（B-树）是一种平衡的多路查找树。2-3树和2-3-4树都是B树的特例。节点最大的孩子数组称为B树的阶（order），因此，2-3树是3阶B树，2-3-4树是4阶B树。 

（一）m阶下的B树

一棵m阶的B树满足下列条件：

1.树中每个结点至多有m个孩子。

2.除根结点和叶子结点外，其它每个结点至少有m/2个孩子。

3.根结点至少有2个孩子（如果B树只有一个结点除外）,这条性质是由B树的插入分裂策略决定的。

4.所有叶结点在同一层，B树的叶结点可以看成一种外部节点，不包含任何信息。

4.有k个关键字(关键字按递增次序排列)的非叶结点恰好有k+1个孩子。

5.一个节点如果由n个关键字，则节点内数据结构为P0，K1，P1，K2，P2.........Pn-1 Kn Pn 其中 p为指向其子节点的指针，因为父子的大小 关系和节点内大小关系，满足Kj 大于Pj指针所指向的子树上的所有关键字小雨Pj+1指针所指向子树上的所有关键字

（二）t度下的B树

一棵最小度为t的B树是满足如下四个条件的平衡多叉树：

1.每个节点最多包含2t−1个关键字；除根节点外的每个节点至少有t−1个关键字（t≥2），根节点至少有一个关键字；

2.一个节点u中的关键字按非降序排列：u.key1≤u.key2≤…u.keynu.key1≤u.key2≤…u.keyn；

3.每个节点的关键字对其子树的范围分割。设节点uu有n+1个指针，指向其n+1棵子树，指针为u.p1,…u.pn，关键字ki为u.pi所指的子树中的关键字，有k1≤u.key1≤k2≤u.key2…k1≤u.key1≤k2≤u.key2…成立；

4.所有叶子节点处于同一层次。这表明B树是平衡的。平衡性其实正是B树名字的来源，B表示的正是单词Balanced；

比如说要查找7，首先从外存读取得到根节点3,5,8三个元素，发现7不在，但是5、8之间，因此就通过A2再读取外存的6,7节点找到结束。

B树的插入和删除和2-3树、2-3-4树类似。

（三）度与阶的关系

t度 的B树就是 2t阶 的B树(这也是B树的分裂机制决定的)：

2t-1为奇数为存储的索引数据，2t偶数为指针指向子树。当裂变之后两边子树各自分配到t个指针

因为t度的B树节点最多有2t个孩子，2t-1个关键字；m阶的B树最多有m个孩子，

其实通过度定义的B树和通过阶数定义的B树，区别就是一个是用的这个B树节点的最小度数一个是用的这个树节点的最大度数。

二：用途

B树的数据结构为内外存的数据交互准备的

当要处理的数据很大时，无法一次全部装入内存。
这时对B树调整，使得B树的阶数与硬盘存储的页面大小相匹配。
比如说一棵B树的阶为1001（即1个节点包含1000个关键字），高度为2（从0开始），它可以存储超过10亿个关键字（1001x1001x1000+1001x1000+1000）,
只要让根节点持久的保留在内存中，那么在这颗树上，寻找某一个关键字至多需要两次硬盘的读取即可。

三：性能

对于n个关键字的m阶B树，最坏情况查找次数计算 

第一层至少1个节点，第二层至少2个节点，由于除根节点外每个分支节点至少有⌈m/2⌉棵子树，则第三层至少有2x⌈m/2⌉个节点...
这样第k+1层至少有2x(⌈m/2⌉)^(k-1),实际上，k+1层的节点就是叶子节点。
若m阶B树有n个关键字，那么当你找到叶子节点，其实也就等于查找不成功的节点为n+1，
因此n+1>=2x(⌈m/2⌉)^(k-1),即 

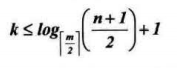
在含有n个关键字的B树上查找时，从根节点到关键字节点的路径上涉及的节点数不超多