数据结构（六）查找---多路查找树（2-3树）

前提

多路查找树-B树

普通树或二叉树等一个结点只能存一个元素，比如BST、AVL、红黑等都是为了内存而设计；
B树每个结点可以有n个元素和n+1个孩子，减少树的高度，减少树的度，所以可以降低内存读取外存的次数；( 对二叉查找树的改进。它的设计思想是，将相关数据尽量集中在一起，以便一次读取多个数据，减少硬盘操作次数）。
B树为了 磁盘 或其它 存储设备 而设计的一种 多叉平衡查找树；

多路查找树(muitl-way search tree)，其每一个节点的孩子数可以多于两个，且每一个节点处可以存储多个元素。主要有4中特殊形式。2-3树，2-3-4树，B树，B+树

一：2-3树

（一）定义

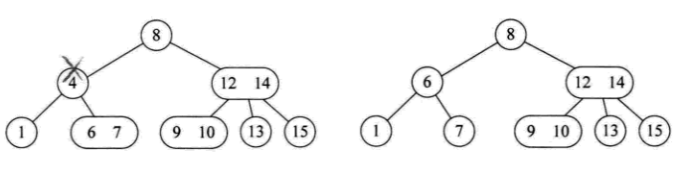
其中的每一个节点都具有两个孩子（称为2节点）或者三个孩子（称为3节点）。 
并且2-3树中所有的叶子都在同一层上。
一个2节点包含一个元素和两个孩子（或者没有孩子）。
一个3节点包含一小一大两个元素和三个孩子（或者没有孩子）。 

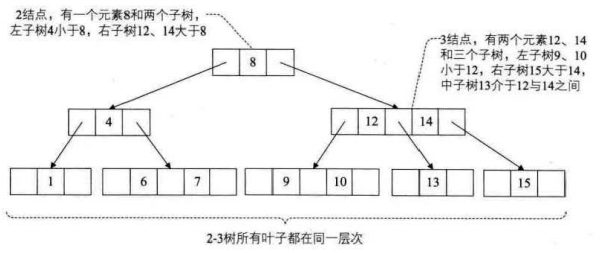
（二）2-3树的插入实现（含分裂）

（1）对于空树，插入一个2节点即可；

（2）插入节点到一个2节点的叶子上。由于本身就只有一个元素，所以只需要将其升级为3节点即可。

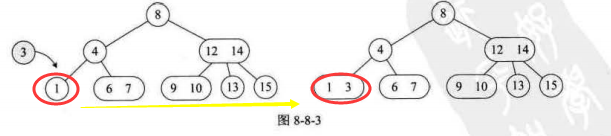
（3）插入节点到一个3节点的叶子上。因为3节点本身最大容量，因此需要拆分，且将树中两元素或者插入元素的三者中选择其一向上移动一层。 （复杂，分情况）

三种情况：

1）升级父节点

2）升级根节点 （一条路上的父节点都变为3结点，只有去找根）

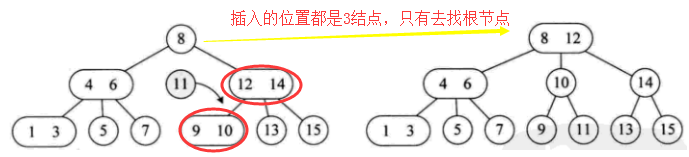
3）增加树高度（当我们根节点也变为3结点后，我们就要去升级树的高度）

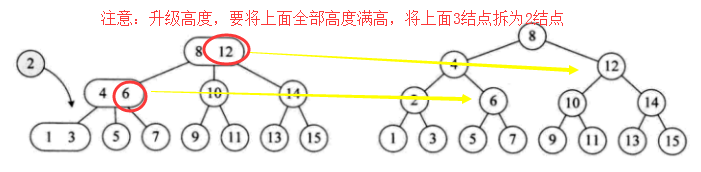
（三） 2-3树的删除实现（含合并）

（1）所删元素位于一个3节点的叶子节点上，直接删除，不会影响树结构。 

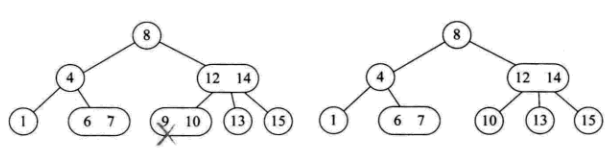
（2）所删元素位于一个2节点上，直接删除，破坏树结构，所以需要分情况讨论

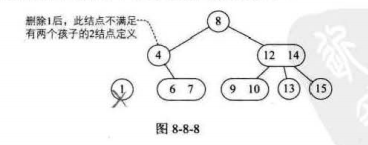
分4种情况

1）此节点双亲也是2节点，且拥有一个3节点的右孩子； 

2）此节点的双亲是2节点，它右孩子也是2节点；

3）此节点的双亲是3节点； 

4）当前树是一个满二叉树，降低树高； 

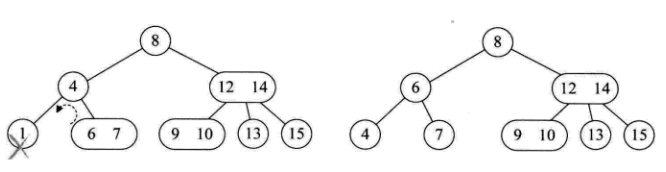
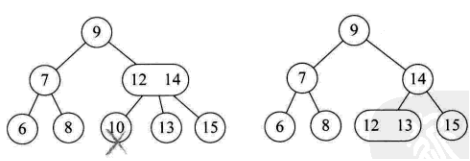
（3）所删元素位于非叶子的分支节点。此时按树中序遍历得到此元素的前驱或后续元素，补位

分两种情况

1）分支节点是2节点 

2）分支节点是3节点