数据结构（六）查找---线性索引查找

前提

我们前面提到的几种高效查找方法都是基于有序的基础上的，但是实际上，很多数据集可能增长非常快。例如空间动态信息等，
对于这样的查找表，我们若是保证记录全部按照当中某个关键字有序，其维护的时间代价非常高，
所以这种数据通常是按照先后顺序存储。

对于这样的查找表，我们如何快速的查找到所需要的数据？---》通过索引

数据结构的最终目的就是提高数据的处理速度，索引是为了加快查找速度而设计的一种数据结构。索引就是把一个关键字与他对应的记录相关联的过程

一个索引由若干个索引项构成，每个索引项至少应包含关键字和其对应的记录在存储器中的位置等信息。

索引技术是组织大型数据库以及磁盘文件的一种重要技术。

索引按照结构可以分为线性索引，树形索引和多级索引。

所谓线性索引就是将索引项集合组织为线性结构，也称为索引表。

下面我们需要了解三种线性索引索引方式：稠密索引，分块索引和倒排索引

一：稠密索引

稠密索引文件的每个记录都有一个索引项，记录在数据区存放是任意的，但索引是按序的，这种索引称为稠密索引。

稠密索引是指在线性索引中，将数据集中的每个记录对应一个索引项。

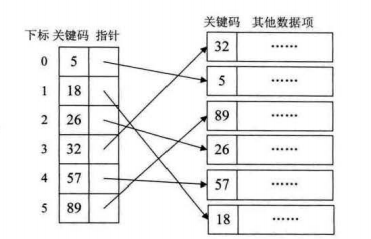
由上图可以知道：对于稠密索引这个索引表而言，索引项一定是按照关键码有序的排列。

优点

索引项有序也就意味着，我们要查找关键字时，可以用折半，插值及斐波那契等有序查找算法。

比如要查找关键字18的记录，如果直接从右侧的数据表中查找，那只能顺序查找。

需要查找6次才可以看到结果

而如果是从侧的索引表中查找，只需两次折半查找就可以得到18对应的指针。对应找到结果。

好吧！以上显然是稠密所以优点。

缺点

如果数据集非常大，比如上亿，那也就意味着索引也得同样的数据集长度规模。

对于内存有限的计算机来说，可能就需要反复去访问磁盘，查找性能大大下降。

稠密索引文件的索引查找、更新都较方便，但由于索引项多，占用空间较大。

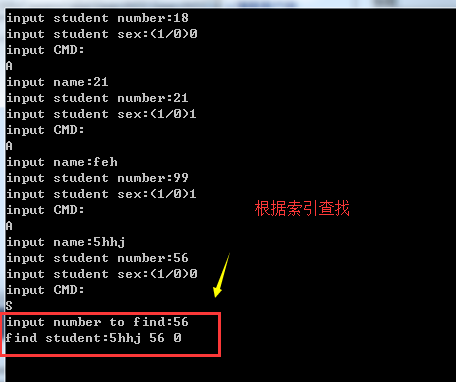
案例实现：年级最多1000个学生，现在进行稠密索引

#define MAXSIZE 1000

typedef struct _Student        //记录
{
    int No;
    char name[32];
    bool sex;
    struct _Student* next;
}Student;    

typedef struct _Index    //索引
{
    int No;
    Student* ind;
}Index;

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>

#define MAXSIZE 1000

typedef struct _Student        //记录
{
    int No;
    char name[32];
    bool sex;
    struct _Student* next;
}Student;    

typedef struct _Index
{
    int No;
    Student* ind;
}Index;

Student* S;
Index I[MAXSIZE];

void AddInfo(int No, char* name, int sex)
{
    //创建数据
    Student *ST;
    int loc,i;
    ST = (Student *)malloc(sizeof(Student));
    strcpy(ST->name, name);
    ST->No = No;
    ST->sex = sex;
    ST->next = S;
    S = ST;
    //插入索引

    if (Insert_Search(I, I[0].No, ST->No, &loc)==-1)
    {
        for (i = I[0].No + 1; i > loc; i--)
        {
            I[i].No = I[i - 1].No;
            I[i].ind = I[i - 1].ind;
        }

        I[i].No = ST->No;
        I[i].ind = ST;

        I[0].No++;    //存储数组大小
    }
}

int Search_Info(int no,Student** stu)
{
    int loc;
    loc = Insert_Search(I, I[0].No, no, &loc);
    if (loc != -1)
        *stu = I[loc].ind;
    else
        return -1;
    return 1;
}

int Insert_Search(Index *ind, int n, int key,int *loc)
{
    int low, high, mid;
    low = 1;
    high = n;
    if (n <= 1)
        mid = n+1;
    if (key<I[low].No)
    {
        *loc = low;
        return -1;
    }
    else if (key > I[high].No)
    {
        *loc = high + 1;
        return -1;
    }
    else
    {
        while (low < high)
        {
            mid = low + (key - ind[low].No) / (ind[high].No - ind[low].No)*(high - low);
            if (ind[mid].No < key)
                low = mid + 1;
            else if (ind[mid].No>key)
                high = mid - 1;
            else
                return mid;
        }
        mid++;
    }
    *loc = mid;

    return -1;
}

int main()
{
    char name[32];
    int no;
    int sex;
    char cmd;
    Student* info;
    I[0].No = 0;

    while (1)
    {
        printf("input CMD:\n");
        scanf("%c", &cmd);
        switch (cmd)
        {
        case 'A':
            printf("input name:");
            scanf("%s", name);
            printf("input student number:");
            scanf("%d", &no);
            printf("input student sex:(1/0)");
            scanf("%d", &sex);
            AddInfo(no, name, sex);
            break;
        case 'S':
            printf("input number to find:");
            scanf("%d", &no);
            if (Search_Info(no, &info) == 1)
                printf("find student:%s %d %d", info->name, info->No, info->sex);
            else
                printf("no find");
            break;
        case 'Q':
            exit(0);
        default:
            break;
        }
        getchar();
    }

}

二：分块索引

注意理解：稠密索引是因为索引项和数据集的记录个数相同，所以空间代价很大。

 如何减少索引项的个数呢？

我们可以对数据集进行分块，使其分块有序，然后再对每一块建立一个索引项（类似于图书馆的分块）。

前提：

分块有序是把数据集的记录分成了若干块，并且这些块需要满足两个条件：

（1）块内无序

每一块内的记录不要求有序

（2）块间有序

比如要求第二块所以记录的关键字均要大于第一块中所有记录的关键字，第三块要大于第二块。

只有块间有序才有可能在查找时带来效率。

对于分块有序的数据集，将每块对应一个索引项，这种索引方法叫做分块索引。

结构

分块索引的索引项结构分为三个数据项：

a: 最大关键码--存储每一块中的最大关键字。

b: 存储每一块中记录的个数以便于循环时使用。

c: 用于指向块首数据元素的指针，便于开始对这一块中记录进行遍历。

查找

在分块索引表中查找，可以分为两步：

a: 在分块索引表中查找要查的关键字所在块。

由于分块索引表是块间有序的，因此很容易利用折半插值等算法得到结果。

b:根据块首指针找到相应的块，并在块中顺序查找关键码。

因为块中可以是无序的，因此只能顺序查找。

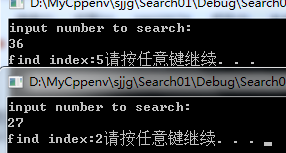
代码实现：结合二分查找和顺序查找

数据源于上图

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>

#define MAXSIZE 100

typedef struct _blockIndex
{
    int key;
    int len;
    int *first;
}blockInfo,BlockIndex[MAXSIZE];

int Binary_Search(BlockIndex B, int key, int n,int *loc)
{
    int low, high, mid;
    low = 0;
    high = n-1;
    while (low<=high)
    {
        mid = (high + low) / 2;
        if (B[mid].key == key)
            return mid;
        else if (B[mid].key < key)
            low = mid + 1;
        else
            high = mid - 1;
    }
    if (B[mid].key < key&&key < B[mid + 1].key)
        *loc = mid + 1;
    else
        *loc = mid;
    return -1;
}

int main()
{
    int a[9] = { 18, 5, 27, 13, 57, 36, 96, 62, 77 };
    BlockIndex BI;
    int n,loc,ret;
    //初始化分块索引
    BI[0].key = 27;
    BI[0].len = 4;
    BI[0].first = a;

    BI[1].key = 57;
    BI[1].len = 2;
    BI[1].first = a+4;

    BI[2].key = 96;
    BI[2].len = 3;
    BI[2].first = a + 6;

    printf("input number to search:\n");
    scanf("%d", &n);
    ret = Binary_Search(BI, n, 3, &loc);
    if (ret != -1)
        loc = ret;
    for (int i = BI[loc].first - a; i < BI[loc].first - a + BI[loc].len; i++)
        if (a[i] == n)
        {
            printf("find index:%d", i);
            break;
        }

    system("pause");
    return 0;
}

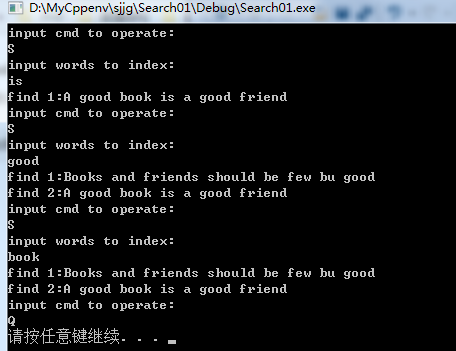
三：倒排索引

倒排索引1

倒排索引2

最基础的搜索技术

案例：

忽略大小写和复数，得出单词表，找到他们分别出现在哪篇文章中

我们输入某个单词，就能够索引处对应的文章，而且由于单词有序，索引很快，根据单词直接找到文章，所以整体速度很快。但是当文章数量一大，就难以实现

其中记录号表存储具有相同次关键字的所有记录的记录号（可以是指向记录的指针或者是该记录的主关键字）。这种索引方法就是倒排索引

查找快，维护困难

代码实现

typedef struct _wordsRec
{
    char word[32];
    int record[10];
}wordsRec, WordsRec[MAXSIZE];

void createTable(WordsRec WR)
{
    strcpy(WR[0].word, "a");
    WR[0].record[0] = 2;

    strcpy(WR[1].word, "and");
    WR[1].record[0] = 1;

    strcpy(WR[2].word, "be");
    WR[2].record[0] = 1;

    strcpy(WR[3].word, "book");
    WR[3].record[0] = 1;
    WR[3].record[1] = 2;

    strcpy(WR[4].word, "but");
    WR[4].record[0] = 1;

    strcpy(WR[5].word, "few");
    WR[5].record[0] = 1;

    strcpy(WR[6].word, "friend");
    WR[6].record[0] = 1;
    WR[6].record[1] = 2;

    strcpy(WR[7].word, "good");
    WR[7].record[0] = 1;
    WR[7].record[1] = 2;

    strcpy(WR[8].word, "is");
    WR[8].record[0] = 2;

    strcpy(WR[9].word, "should");
    WR[9].record[0] = 1;
}

int Binary_Search(WordsRec WR, int n, char *str)
{
    int low, high,mid;
    low = 0; 
    high = n-1;
    while (low<=high)
    {
        mid = (low + high) / 2;
        if (strcmp(WR[mid].word, str) > 0)
            high = mid - 1;
        else if (strcmp(WR[mid].word, str) < 0)
            low = low + 1;
        else
            return mid;
    }
    return -1;
}

int main()
{
    int i, index;
    char cmd;
    char arti[2][50] = {
        "Books and friends should be few bu good",
        "A good book is a good friend"
    };
    char words[32];

    WordsRec WR;
    for (i = 0; i < MAXSIZE;i++)
        memset(WR[i].record, 0, 10 * sizeof(int));

    createTable(WR);

    while (1)
    {
        printf("input cmd to operate:\n");
        scanf("%c",&cmd);
        if (cmd=='Q')
            break;
        printf("input words to index:\n");
        scanf("%s", words);
        index = Binary_Search(WR, 10, words);
        if (index == -1)
            printf("no found\n");
        else
        {
            for (i = 0; WR[index].record[i]!=0;i++)
                printf("find %d:%s\n", i + 1, arti[WR[index].record[i]-1]);
        }
        getchar();
    }

    system("pause");
    return 0;
}