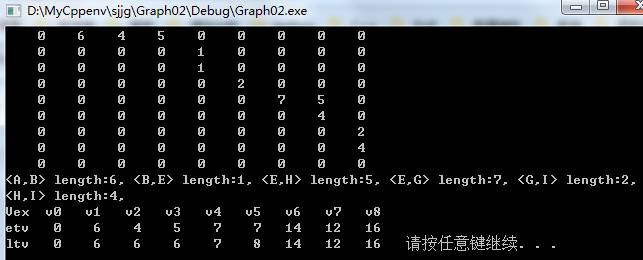
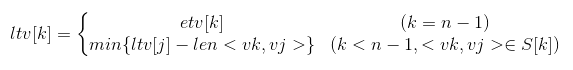一:定义
(一)最短时间
我们要对一个流程图获得最短时间,就要分析他们的拓扑关系,并且找到当中的最关键的流程,这个流程的时间就是最短时间
(二)AOE网(Activity On Edge Network)
在一个表示工程的带权有向图中,用到的表示时间,用有向边表示活动,用边上权值表示活动的持续时间,这种有向图的边表示活动的网,我们称之为AOE网
我们将AOE网中没有入边的顶点称为源点或始点,没有出边的顶点称为终点或者汇点
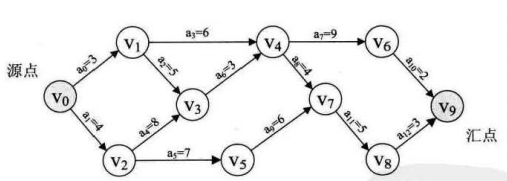
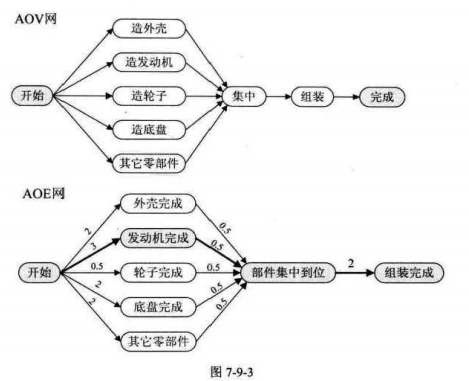
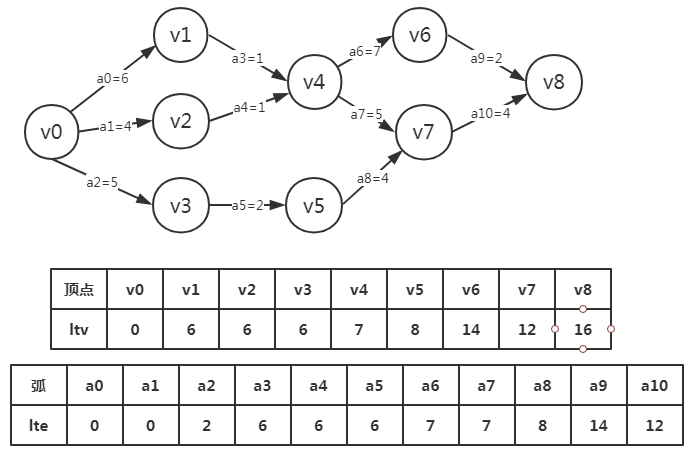
例如下图AOE网,
v0为源点,表示整个工程的开始,v9为终点,表示这个工程的结束。
顶点v0,v1,....v9分别表示事件
弧<v0,v1>,<v0,v2>,...,<v8,v9>都表示一个活动,用a0,a1,...,a12表示
补充:相比于AOV网
AOV中不在意边的权值,不局限一个源点和一个终点,关注的是是否构成环
AOE关注边的权值,来求得最短时间等信息,源点和终点都只有一个
(三)关键路径
路径上各个活动所持续的事件之和称为路径长度,从源点到终点具有最大长度的路径叫关键路径,在关键路径上的活动叫关键活动
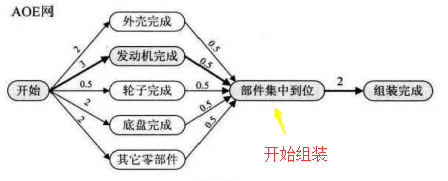
例如我们开始组装时候,我们就要等到前面的所有装备工作全部完成(按照最长路径来算),才能开始我们的组装任务。所以我们的关键路径需要是最大长度的路径
二:AOE和AOV(活动和事件|顶点与弧)
AOE网是表示工程流程的,所以它就具有明显的工程的特性。
只有在某顶点所表示的事件发生后,从该顶点出发的各活动才能开始。
只有在进入某顶点的各活动都已经结束,该顶点所代表的事件才能发生。
AOE与AOV对比
虽然都是用来对工程建模,但是还是有很大不同。主要体现在:
AOV网是顶点表示活动的网,他只描述活动之间的制约更新,
AOE网是用边表示活动的网,边上的权值表示活动持续的时间
AOE网是要建立在活动之间制约关系没有矛盾的基础之上,再来分析完成整个工程至少需要多少时间,或者为缩短完成工程所需时间,应该加快哪些活动等问题
三:四个必要参数
(一)事件最早发生时间etv(earliest time of vertex)
(二)事件最晚发生时间ltv(lastest time of vertex)
即顶点Vk的最晚发生时间,也就是每个顶点对应的事件最晚需要开始的事件,超出此事件将会延误整个工期
(三)活动的最早开工时间ete(earliest time of edge)
(四)活动的最晚开工时间lte(lastest time if edge)
即弧的最晚发生时间,也就是不推迟工期的最晚开工时间
总结(重点):
我们可以由事件的最早发生时间和事件的最晚发生时间求出活动的最早和最晚开工时间。
由1,2可以求得3,4,然后在根据ete[k]是否与lte[k]相等来判断ak是否是关键活动
活动的最早开始时间和活动的最晚开始时间,若是相等,就意味着此活动是关键活动
四:案例推导
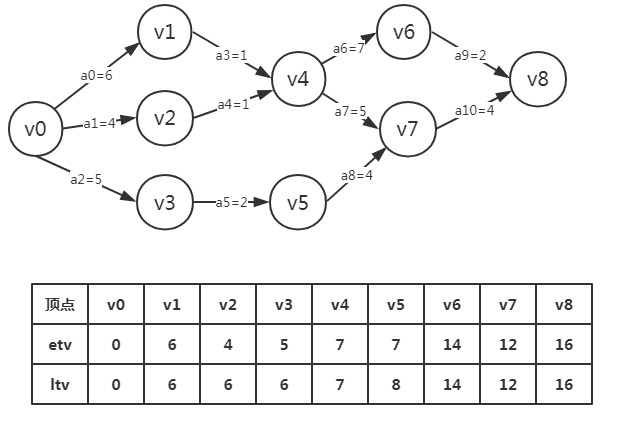
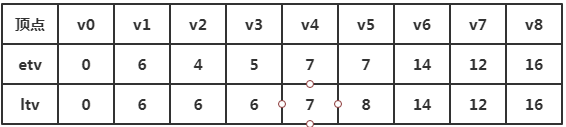
(一)etv从左向右推导

其中P[k]表示所有到达顶点vk的弧的集合。比如P[1]就只有<v0,v1>,P[4]就有<v1,v4>,<v2,v4>是所有以顶点vk为弧头的弧的集合
例如:我们只推导v0-v4
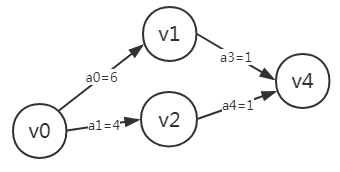
etv[0]=0,因为k=0
etv[1]=6,etv[1]=max{etv[i]+len<vi,vk>},因为<vi,vk>属于P[k],所以i=0,etv[i]=etv[0]+len<v0,v1>=6
etv[2]=4
--------------------------------------------------------------------上面可以看出来--------------------------------------------------------------------
etv[4]的推导,我们先看他的P[k]弧的集合,有<v1,v4>,<v2,v4>两个,所以我们从{etv[1]+len<v1,v4>,etv[2]+len<v2,v4>}集合中选取最大的,就是etv[4]=etv[1]+len<v1,v4>=7

(二)ltv从右向左推导
是在我们得出etv之后,我们利用etv反推ltv。其实就是把拓扑序列倒过来继续的,可以得出计算得到vk即求ltv[k]的最晚发生时间
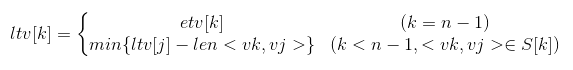
其中n是顶点(事件个数),而我们的数组下标最大为n-1
其中S[k]是表示所有从顶点vk出发的弧的集合。例如下图中S[6]就只是<v6,v8>的集合,S[4]就是<v4,v6>,<v4,v7>两个弧的集合,是以顶点vk为弧尾的弧
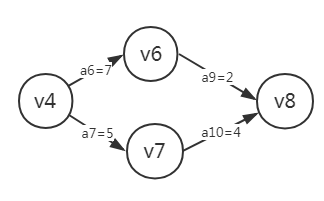
例如:我们推导上图
ltv[8]=etv[8]=16 k=9-1,9是顶点个数
ltv[6]=min{ltv[j]-len<vk,vj>},其中以v6为弧尾的弧只有一条,<v6,v8>,是以ltv[6]=ltv[8]-len<v6,v8>=14
ltv[7]同上为12
---------------------------------------------------------下面推导v4-------------------------------------------------------
ltv[4]中以v4为弧尾的弧有:<v4,v6>和<v4,v7>,所以我们需要比较ltv[6]-len<v4,v6>,和ltv[7]-len<v4,v7>
其中ltv[6]-len<v4,v6>=7,ltv[7]-len<v4,v7>7,所以v4就是7
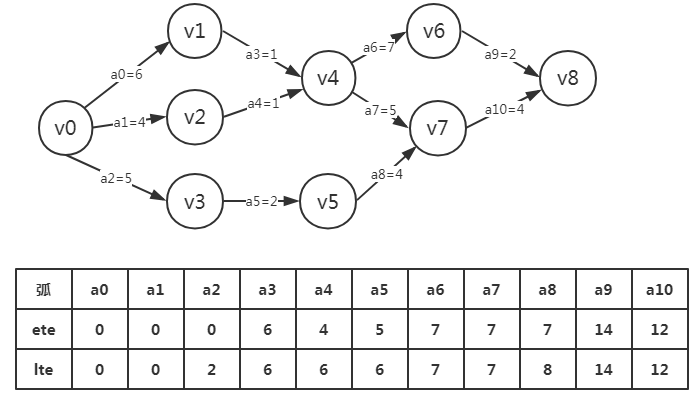
(三)ete:活动最早开工时间需要和etv事件最早发生时间结合
因为前面说了:只有在某顶点所表示的事件发生后,从该顶点出发的各活动才能开始。
所以我们要获取某个活动的最早开始时间,我们就要知道,发起该活动的事件的最早开始时间,只有事件一开始,活动才进行,就相当于口哨一响起来,我们就开始跑步
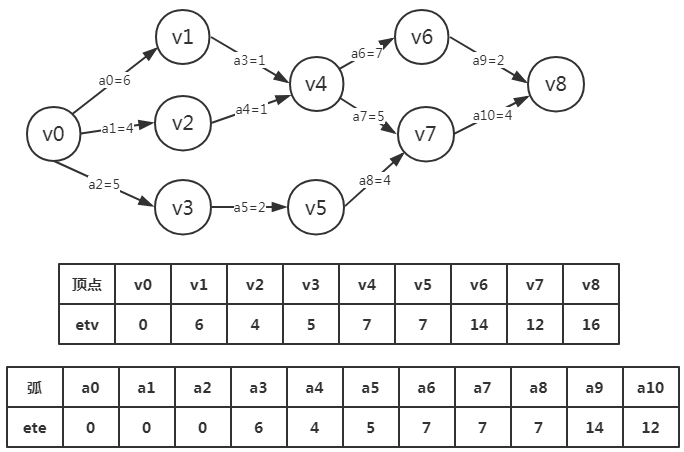
活动a0,a1,a2全部由事件v0发起,所以我们的活动最早开始时间是elv[0]
活动a3的发起者事件是v1,所以我们最早开始时间就是elv[1]=6
活动a4的发起者事件是v2,所以活动最早开始时间是elv[2]=4
.....
(四)lte:活动最晚开工时间需要和ltv事件最晚发生时间结合(都是倒序获得)
活动的最晚发生时间取决于弧所指向的事件的最晚开始时间-活动的持续时间
例如:
a9指向v8,所以获得a9的最晚开工时间是ltv[8]-len<a8>=16-2=14
a10也是指向v8,所以a10的最晚开工时间是ltv[8]-len<a10>=16-4=12
.....
总结:AOE网中活动的最早/最晚开工时间取决于事件的最早/最晚开始时间,所以我们求出etv和ltv就可以获取ete和lte
五:算法实现
(一)求elv数组
int *etv, *ltv; //事件最早发生时间和最晚发生时间数组
int *stack2; //用于存储拓扑序列的栈,因为几乎是etv,ltv,ete,lte数组求取都需要拓扑序列,所以我们将它存储在全局变量中
int top2; //用于stack2的指针,后面求关键路径时需要
改进后的拓扑序列算法:在判断是否有回路时,获取全部拓扑序列放入全局栈stack2中,同时将获取到etv数组内容
Status TopologicalSort(AdjGraphList AG)
{
EdgeNode* e;
int i, j, k, gettop;
int count = 0; //用于统计输出顶点个数
int top = -1; //这是我们要创建的栈的指针
int *stack = (int*)malloc(sizeof(int)*AG.numVertexes); //这是我们创建的临时栈
//最开始将所有入度为0的顶点入栈
for (i = 0; i < AG.numVertexes; i++)
if (!AG.adjlist[i].in)
stack[++top] = i;
//初始化全局数组stack2,etv,ltv
top2 = -1;
etv = (int *)malloc(AG.numVertexes*sizeof(int));
for (i = 0; i < AG.numVertexes; i++)
etv[i] = 0; //初始化为0
stack2 = (int *)malloc(sizeof(int)*AG.numVertexes);
//下面进入主循环,直到栈中无数据结束
while (top != -1)
{
//出栈数据
gettop = stack[top--]; //出栈
count++;
stack2[++top2] = gettop; //将弹出的栈顶序号压入拓扑序列的栈中,将每一个顶点事件都入栈,变为拓扑序列
//对他出栈数据的所有邻接点的入度减一
for (e = AG.adjlist[gettop].firstedge; e; e = e->next)
{
k = e->adjvex;
if (!(--AG.adjlist[k].in))
stack[++top] = k;
if ((etv[gettop] + e->weight) > etv[k]) //求各个顶点事件最早发生时间
etv[k] = etv[gettop] + e->weight;
}
}
//进行判断,若是count小于顶点数,则有环
if (count < AG.numVertexes)
return ERROR;
return OK;
}
解释:第三处的红线代码
if ((etv[gettop] + e->weight) > etv[k]) //求各个顶点事件最早发生时间
etv[k] = etv[gettop] + e->weight;

其中gettop是顶点v[i]的下标,而k就是顶点v[i]的邻接点的下标k = e->adjvex;可以看做v[k],我们获取的就是etv[k]
(二)求ltv数组
EdgeNode* e;
int i, j, k, gettop;
int ete, lte; //声明获得最早发生时间和最迟发生时间变量
TopologicalSort(AG); //求得拓扑序列,获得etv数组和stack2数组
ltv = (int *)malloc(sizeof(int)*AG.numVertexes); //事件最晚发生时间数组
for (i = 0; i < AG.numVertexes; i++)
ltv[i] = etv[AG.numVertexes - 1]; //全部初始化为倒序第一个
while (top2!=-1)
{
gettop = stack2[top2--]; //倒序获取每个顶点,从终点开始,由于终点都没有邻接点,所以我们不会修改数据,始终保持etv[n-1],公式情况一
//根据求ltv的公式,我们开始补全ltv数组
for (e = AG.adjlist[gettop].firstedge; e;e=e->next) //这个for循环针对的是非终点,有出度边,情况二
{
k = e->adjvex; //k是他的下一个邻接点的下标,我们会修改他,按照情况二
if (ltv[k] - e->weight < ltv[gettop]) //求各个顶点事件的最晚发生时间
ltv[gettop] = ltv[k] - e->weight;
}
}
(三)求ete,lte和关键活动
活动的最早开始时间和活动的最晚开始时间,若是相等,就意味着此活动是关键活动
根据前面求得的etv和ltv,我们可以获取活动的最早和最晚开始时间,然后对其进行对比,即可判断是否在关键路径上
另外注意:这里的ete和lte是获得是针对边,所以我们操作的是出度边集
for (i = 0; i < AG.numVertexes;i++) //i代表顶点下标
{
for (e = AG.adjlist[i].firstedge; e;e=e->next)
{
k = e->adjvex; //获取邻接点
ete = etv[i]; //ete是由顶点i发起的活动,这是其活动最早开始时间
lte = ltv[k] - e->weight; //获取其中某一个邻接点的活动最迟发生时间,我们针对一个顶点会对其所有邻接点进行获取判断
//我们获取的是活动,是弧,弧的尾由i结点,头由k决定
if (ete==lte)
printf("<%c,%c> length:%d, ", AG.adjlist[i].data, AG.adjlist[k].data, e->weight);
}
}
(四)全部代码


#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <stdbool.h>
#define MAXVEX 100 //最大顶点数
#define INFINITY 65535 //用0表示∞
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
typedef int Status;
typedef char VertexType; //顶点类型,字符型A,B,C,D...
typedef int EdgeType; //边上权值类型10,15,...
//邻接矩阵结构
typedef struct
{
VertexType vers[MAXVEX]; //顶点表
EdgeType arc[MAXVEX][MAXVEX]; //邻接矩阵,可看作边表
int numVertexes, numEdges; //图中当前的顶点数和边数
}MGraph;
typedef struct EdgeNode //边表结点
{
int adjvex;
int weight;
struct EdgeNode* next;
}EdgeNode;
typedef struct VertexNode //顶点表结点
{
int in;
VertexType data;
EdgeNode* firstedge;
}VertexNode, AdjList[MAXVEX];
//邻接表结构
typedef struct
{
AdjList adjlist;
int numVertexes, numEdges; //图中当前的顶点数和边数
}AdjGraphList;
int *etv, *ltv; //事件最早发生时间和最晚发生时间数组
int *stack2; //用于存储拓扑序列的栈
int top2; //用于stack2的指针,后面求关键路径时需要
//创建邻接矩阵
void CreateMGraph(MGraph* G);
//显示邻接矩阵
void showGraph(MGraph G);
//邻接矩阵转邻接表
void MGragp2AdjList(MGraph G, AdjGraphList* AG);
//拓扑排序
Status TopologicalSort(AdjGraphList AG);
//获取求ete,lte和关键活动
void CriticalPath(AdjGraphList AG);
//显示事件的最早和最晚发生时间
void ShowVertexTime(int n);
int main()
{
MGraph MG;
AdjGraphList AG;
CreateMGraph(&MG);
showGraph(MG);
MGragp2AdjList(MG, &AG);
CriticalPath(AG);
ShowVertexTime(AG.numVertexes);
system("pause");
return 0;
}
//生成邻接矩阵
void CreateMGraph(MGraph* G)
{
int i, j, k, w;
G->numVertexes = 9;
G->numEdges = 11;
//读入顶点信息
G->vers[0] = 'A';
G->vers[1] = 'B';
G->vers[2] = 'C';
G->vers[3] = 'D';
G->vers[4] = 'E';
G->vers[5] = 'F';
G->vers[6] = 'G';
G->vers[7] = 'H';
G->vers[8] = 'I';
//getchar(); //可以获取回车符
for (i = 0; i < G->numVertexes; i++)
for (j = 0; j < G->numVertexes; j++)
G->arc[i][j] = INFINITY; //邻接矩阵初始化
//创建了有向邻接矩阵
G->arc[0][1] = 6;
G->arc[0][2] = 4;
G->arc[0][3] = 5;
G->arc[1][4] = 1;
G->arc[2][4] = 1;
G->arc[3][5] = 2;
G->arc[4][6] = 7;
G->arc[4][7] = 5;
G->arc[5][7] = 4;
G->arc[6][8] = 2;
G->arc[7][8] = 4;
}
//显示邻接矩阵
void showGraph(MGraph G)
{
for (int i = 0; i < G.numVertexes; i++)
{
for (int j = 0; j < G.numVertexes; j++)
{
if (G.arc[i][j] != INFINITY)
printf("%5d", G.arc[i][j]);
else
printf(" 0");
}
printf("\n");
}
}
void MGragp2AdjList(MGraph G, AdjGraphList* AG)
{
int i, j;
EdgeNode* edge;
AG->numEdges = G.numEdges;
AG->numVertexes = G.numVertexes;
for (i = 0; i < G.numVertexes; i++)
{
AG->adjlist[i].data = G.vers[i];
AG->adjlist[i].in = 0;
AG->adjlist[i].firstedge = NULL;
}
for (i = 0; i < G.numVertexes; i++)
{
for (j = 0; j < G.numVertexes; j++)
{
if (G.arc[i][j] != INFINITY)
{
edge = (EdgeNode*)malloc(sizeof(EdgeNode));
edge->adjvex = j;
edge->weight = G.arc[i][j];
edge->next = AG->adjlist[i].firstedge;
AG->adjlist[i].firstedge = edge;
AG->adjlist[j].in++;
}
}
}
}
Status TopologicalSort(AdjGraphList AG)
{
EdgeNode* e;
int i, j, k, gettop;
int count = 0; //用于统计输出顶点个数
int top = -1; //这是我们要创建的栈的指针
int *stack = (int*)malloc(sizeof(int)*AG.numVertexes); //这是我们创建的临时栈
//最开始将所有入度为0的顶点入栈
for (i = 0; i < AG.numVertexes; i++)
if (!AG.adjlist[i].in)
stack[++top] = i;
//初始化全局数组stack2,etv,ltv
top2 = -1;
etv = (int *)malloc(AG.numVertexes*sizeof(int));
for (i = 0; i < AG.numVertexes; i++)
etv[i] = 0; //初始化为0
stack2 = (int *)malloc(sizeof(int)*AG.numVertexes);
//下面进入主循环,直到栈中无数据结束
while (top != -1)
{
//出栈数据
gettop = stack[top--]; //出栈
count++;
stack2[++top2] = gettop; //将弹出的栈顶序号压入拓扑序列的栈中
//对他出栈数据的所有邻接点的入度减一
for (e = AG.adjlist[gettop].firstedge; e; e = e->next)
{
k = e->adjvex;
if (!(--AG.adjlist[k].in))
stack[++top] = k;
if ((etv[gettop] + e->weight) > etv[k]) //求各个顶点事件最早发生时间
etv[k] = etv[gettop] + e->weight;
}
}
//进行判断,若是count小于顶点数,则有环
if (count < AG.numVertexes)
return ERROR;
return OK;
}
void CriticalPath(AdjGraphList AG)
{
EdgeNode* e;
int i, j, k, gettop;
int ete, lte; //声明获得最早发生时间和最迟发生时间变量
TopologicalSort(AG); //求得拓扑序列,获得etv数组和stack2数组
ltv = (int *)malloc(sizeof(int)*AG.numVertexes); //事件最晚发生时间数组
for (i = 0; i < AG.numVertexes; i++)
ltv[i] = etv[AG.numVertexes - 1]; //全部初始化为倒序第一个
while (top2!=-1)
{
gettop = stack2[top2--]; //倒序获取每个顶点,从终点开始,由于终点都没有邻接点,所以我们不会修改数据,始终保持etv[n-1],公式情况一
//根据求ltv的公式,我们开始补全ltv数组
for (e = AG.adjlist[gettop].firstedge; e;e=e->next) //这个for循环针对的是非终点,有出度边,情况二
{
k = e->adjvex; //k是他的下一个邻接点的下标,我们会修改他,按照情况二
if (ltv[k] - e->weight < ltv[gettop]) //求各个顶点事件的最晚发生时间
ltv[gettop] = ltv[k] - e->weight;
}
}
for (i = 0; i < AG.numVertexes;i++) //i代表顶点下标
{
for (e = AG.adjlist[i].firstedge; e;e=e->next)
{
k = e->adjvex; //获取邻接点
ete = etv[i]; //ete是由顶点i发起的活动,这是其活动最早开始时间
lte = ltv[k] - e->weight; //获取其中某一个邻接点的活动最迟发生时间,我们针对一个顶点会对其所有邻接点进行获取判断
//我们获取的是活动,是弧,弧的尾由i结点,头由k决定
if (ete==lte)
printf("<%c,%c> length:%d, ", AG.adjlist[i].data, AG.adjlist[k].data, e->weight);
}
}
printf("\n");
}
void ShowVertexTime(int n)
{
int i;
printf("Vex ");
for (i = 0; i < n; i++)
{
printf("v%d ", i);
}
printf("\netv ");
for (i = 0; i < n; i++)
{
printf("%2d ", etv[i]);
}
printf("\nltv ");
for (i = 0; i < n; i++)
{
printf("%2d ", ltv[i]);
}
}
View Code