数据结构(五)图---最短路径(迪杰斯特拉算法)
一:最短路径问题
(一)定义
在网络中,求两个不同顶点之间的所有路径中,边的权值之和最小的那条路径
1.这条路径就是两点之间的最短路径 2.第一个顶点为源点 3.最后一个顶点终点
(二)分类
单源最短路径--->有权,无权--->有向,无向
从某固定源点触发,求其到所有其他顶点的最短路径
多源最短路径
求任意两顶点间的最短路径
可以通过对每个顶点使用一次单源(不是最好)
二:无权图的单源最短路径(有向)
不考虑无向,无向我们使用BFS,进行层次遍历时,就可以获取
(一)定义
按照递增(非递减)的顺序找出各个顶点的最短路径
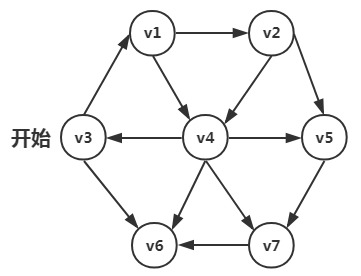
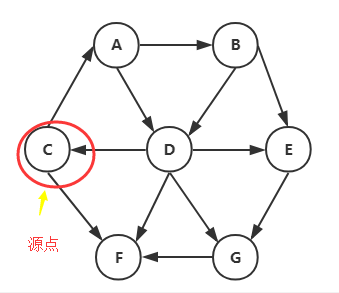
找出视图源点v3到每个顶点的最短路径
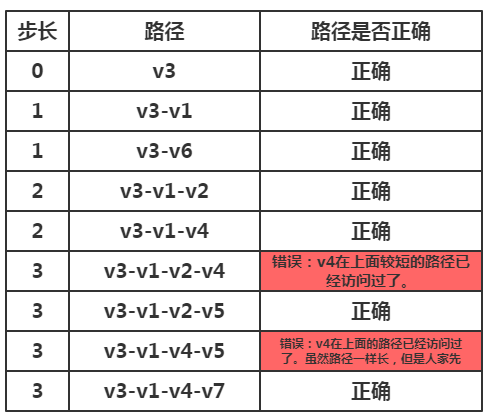
(二)思考
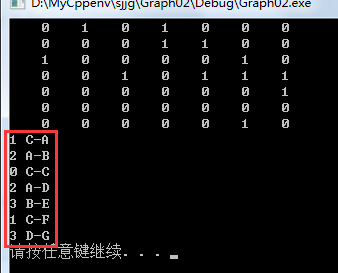
从上图路径表我们可以看出,其路径是按照BFS(有所不同),使用队列进行递增访问各个顶点,从而遍历了所有顶点。
注意:这里我们不使用栈来实现,因为栈用到回溯法,而且使用栈不能很好找到最短路径长
(三)代码实现
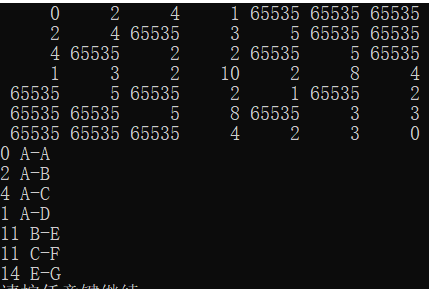
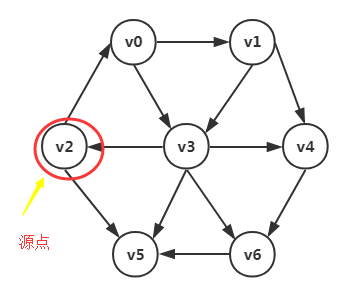
创建邻接矩阵时看这个图 进行结果对比用这个
void unWeight(MGraph G, int s) { int dist[MAXVEX]; //记录达到下标对应顶点的最小距离 int path[MAXVEX]; //记录每个下标对应顶点的前一个经过的顶点 int i, v, w; //生成队列一会使用 LinkQueue Q; InitQueue(&Q); for (i = 0; i < MAXVEX; i++) dist[i] = -1; //全部初始化为-1,表示该顶点未被访问过,没有找到最短路径到这个顶点 //将源点入队 EnQueue(&Q, s); dist[s] = 0; path[s] = s; //将这里设置为他自己是自己的上一步,因为后面根本不会去设置他了 while (!EmptyQueue(Q)) { DeQueue(&Q, &v); for (w = 0; w < G.numVertexes; w++) { if (G.arc[v][w] == 1) //找到邻接点w { if (dist[w] == -1) { dist[w] = dist[v] + 1; path[w] = v; EnQueue(&Q, w); } } } } for (i = 0; dist[i] != -1; i++) //对各个顶点的最短路径长度进行打印,以及他的上一步路径也打印 { printf("%d %c-%c\n", dist[i], G.vers[path[i]], G.vers[i]); } }
(四)全部代码

#pragma once #ifndef _QUEUE_H #define _QUEUE_H #include <stdio.h> #include <stdlib.h> #define OK 1 #define ERROR 0 #define TRUE 1 #define FALSE 0 #define MAXSIZE 100 typedef int ElemType; typedef int Status; typedef struct _qNode { ElemType data; struct _qNode* next; }QNode,*QNodePtr; typedef struct { QNodePtr front,rear; //队头队尾指针 }LinkQueue; Status InitQueue(LinkQueue* Q); Status EnQueue(LinkQueue* Q, ElemType e); Status DeQueue(LinkQueue* Q, ElemType* e); Status EmptyQueue(LinkQueue Q); Status getHead(LinkQueue Q,ElemType* e); #endif

#include "queue.h" Status InitQueue(LinkQueue* Q) { if (!Q) return ERROR; Q->front = Q->rear = (QNodePtr)malloc(sizeof(QNode)); if (!Q->front) return ERROR; Q->front->next = NULL; return OK; } Status EnQueue(LinkQueue* Q, ElemType e) { //尾插法 if (!Q) return ERROR; QNodePtr q = (QNodePtr)malloc(sizeof(QNode)); if (!q) return ERROR; q->data = e; q->next = (*Q).rear->next; (*Q).rear->next = q; Q->rear = q; return OK; } Status DeQueue(LinkQueue* Q, ElemType* e) { QNodePtr q; if (!Q || !e || EmptyQueue(*Q)) return ERROR; q = Q->front->next; Q->front->next = q->next; *e = q->data; if (Q->rear == q) Q->rear = Q->front; free(q); return OK; } Status EmptyQueue(LinkQueue Q) { if (!Q.front->next) return TRUE; return FALSE; } Status getHead(LinkQueue Q,ElemType* e) { QNodePtr q; if (EmptyQueue(Q)) return ERROR; q = Q.front->next; *e = q->data; return OK; }

#define _CRT_SECURE_NO_WARNINGS #include <stdio.h> #include <stdlib.h> #include <string.h> #include <stdbool.h> #include "queue.h" #define MAXVEX 100 //最大顶点数 #define INFINITY 65535 //用0表示∞ typedef char VertexType; //顶点类型,字符型A,B,C,D... typedef int EdgeType; //边上权值类型10,15,... //邻接矩阵结构 typedef struct { VertexType vers[MAXVEX]; //顶点表 EdgeType arc[MAXVEX][MAXVEX]; //邻接矩阵,可看作边表 int numVertexes, numEdges; //图中当前的顶点数和边数 }MGraph; //创建邻接矩阵 void CreateMGraph(MGraph* G); //显示邻接矩阵 void showGraph(MGraph G); //进行最小路径获取 void unWeight(MGraph G); int main() { MGraph MG; CreateMGraph(&MG); showGraph(MG); unWeight(MG,2); system("pause"); return 0; } //生成邻接矩阵 void CreateMGraph(MGraph* G) { int i, j, k, w; G->numVertexes = 7; G->numEdges = 12; //读入顶点信息 G->vers[0] = 'A'; G->vers[1] = 'B'; G->vers[2] = 'C'; G->vers[3] = 'D'; G->vers[4] = 'E'; G->vers[5] = 'F'; G->vers[6] = 'G'; G->vers[7] = 'H'; G->vers[8] = 'I'; //getchar(); //可以获取回车符 for (i = 0; i < G->numVertexes; i++) for (j = 0; j < G->numVertexes; j++) G->arc[i][j] = INFINITY; //邻接矩阵初始化 //创建了有向邻接矩阵 G->arc[0][1] = 1; G->arc[0][3] = 1; G->arc[1][3] = 1; G->arc[1][4] = 1; G->arc[2][0] = 1; G->arc[2][5] = 1; G->arc[3][2] = 1; G->arc[3][4] = 1; G->arc[3][5] = 1; G->arc[3][6] = 1; G->arc[4][6] = 1; G->arc[6][5] = 1; } //显示邻接矩阵 void showGraph(MGraph G) { for (int i = 0; i < G.numVertexes; i++) { for (int j = 0; j < G.numVertexes; j++) { if (G.arc[i][j] != INFINITY) printf("%5d", G.arc[i][j]); else printf(" 0"); } printf("\n"); } } void unWeight(MGraph G, int s) { int dist[MAXVEX]; //记录达到下标对应顶点的最小距离 int path[MAXVEX]; //记录每个下标对应顶点的前一个经过的顶点 int i, v, w; //生成队列一会使用 LinkQueue Q; InitQueue(&Q); for (i = 0; i < MAXVEX; i++) dist[i] = -1; //全部初始化为-1,表示该顶点未被访问过,没有找到最短路径到这个顶点 //将源点入队 EnQueue(&Q, s); dist[s] = 0; path[s] = s; //将这里设置为他自己是自己的上一步,因为后面根本不会去设置他了 while (!EmptyQueue(Q)) { DeQueue(&Q, &v); for (w = 0; w < G.numVertexes; w++) { if (G.arc[v][w] == 1) //找到邻接点w { if (dist[w] == -1) { dist[w] = dist[v] + 1; path[w] = v; EnQueue(&Q, w); } } } } for (i = 0; dist[i] != -1; i++) { printf("%d %c-%c\n", dist[i], G.vers[path[i]], G.vers[i]); } }
三:有权的单源最短路径算法(迪杰斯特拉Dijkstra算法)
(一)了解
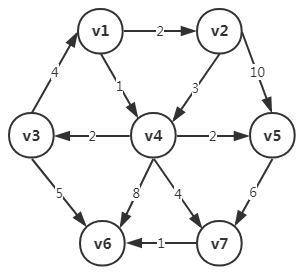
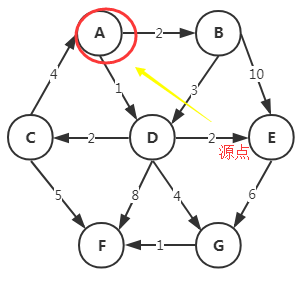
从v1-v6最小为6,即v1-v4-v7-v6。不一定为经过顶点最小的路,和上面的无权最短路径不同
注意:我们不考虑负值圈

会导致一直循环,获取无穷收益。导致所有算法都失效
(二)解决方法
方法和上面的无权路径还是相似的,就是按照递增的顺序找出各个顶点的最短路
(三)迪杰斯特拉Dijkstra算法

#define _CRT_SECURE_NO_WARNINGS #include <stdio.h> #include <stdlib.h> #include <string.h> #include <stdbool.h> #include "queue.h" #define MAXVEX 100 //最大顶点数 #define INFINITY 65535 //用0表示∞ typedef char VertexType; //顶点类型,字符型A,B,C,D... typedef int EdgeType; //边上权值类型10,15,... //邻接矩阵结构 typedef struct { VertexType vers[MAXVEX]; //顶点表 EdgeType arc[MAXVEX][MAXVEX]; //邻接矩阵,可看作边表 int numVertexes, numEdges; //图中当前的顶点数和边数 }MGraph; //创建邻接矩阵 void CreateMGraph(MGraph* G); //显示邻接矩阵 void showGraph(MGraph G); //迪卡斯特拉算法,获取最短路径 void Dijkatra(MGraph G, int s); void Dijkatra(MGraph G,int s) { int path[MAXVEX]; //是数组下标表示的顶点所经历的前一个顶点 int dist[MAXVEX]; //是数组下标表示的顶点的最小权值路径和 //上面两个数组都有作用,和无权最短路径一致,但是无权最短路径可以使用dist是否被设置来判断一个顶点是否被访问, //但是这里无法使用,因为dist和普里姆算法中的lowcost一样,是使用贪心算法时,每到一个顶点,我们都会全部更新dist //所以我们需要另外一个数组来标志各个顶点是否被访问 int final[MAXVEX]; int i,j,k,min; //对数据进行初始化 for (i = 0; i < G.numVertexes;i++) { final[i] = 0; //0表示该数组下标所表示的顶点未被访问 path[i] = 0; //初始化路径数组为0,表示当前每个都是独立的根节点 dist[i] = G.arc[s][i]; //这一步是重点:初始化路径数组的值为起始v0到各个点的权值 } dist[s] = 0; //到源点自己的路径为0 path[s] = s; //设置源点的前一个顶点就是自己 final[s] = 1; //源点被访问过了 //开始主循环,每次求的v0(s)到某个v顶点的最短路径 for (i = 0; i < G.numVertexes;i++) { min = INFINITY; //和普里姆算法相似 for (j = 0; j < G.numVertexes;j++) //由于是有向图所以都要从0开始,找到他的每个邻接点 { if (!final[j]&&dist[j]<min) //若是该顶点没有被访问过,且该点到s点的距离小于min,我们就将min设置为他 { k = j; //记录下该v到s点的下标和min最小路径 min = dist[j]; } } final[k] = 1; //将目前找到的距离v0(S)最近的顶点置为1 for (j = 0; j < G.numVertexes;j++) //修正当前最短路径即距离 { //修正方法就是循环k的每个邻接点,我们作为三角形来看,若是两边之和小于第三边,那我们原来找的那条直接的最短边就失效了,用这两条直接代替 //所以我们将距离修改,路径设置为他的上一步k, if (!final[j]&&(min+G.arc[k][j])<dist[j]) { //说明找到了更短的路径,修改dist和path数组 dist[j] = min + G.arc[k][j]; //修改当前路径长度 path[j] = k; } } } for (i = 0; i<G.numVertexes; i++) { printf("%d %c-%c\n", dist[i], G.vers[path[i]], G.vers[i]); } } int main() { MGraph MG; CreateMGraph(&MG); showGraph(MG); Dijkatra(MG,0); system("pause"); return 0; } //生成邻接矩阵 void CreateMGraph(MGraph* G) { int i, j, k, w; G->numVertexes = 7; G->numEdges = 12; //读入顶点信息 G->vers[0] = 'A'; G->vers[1] = 'B'; G->vers[2] = 'C'; G->vers[3] = 'D'; G->vers[4] = 'E'; G->vers[5] = 'F'; G->vers[6] = 'G'; G->vers[7] = 'H'; G->vers[8] = 'I'; //getchar(); //可以获取回车符 for (i = 0; i < G->numVertexes; i++) for (j = 0; j < G->numVertexes; j++) G->arc[i][j] = INFINITY; //邻接矩阵初始化 //创建了有向邻接矩阵 G->arc[0][1] = 2; G->arc[0][3] = 1; G->arc[1][3] = 3; G->arc[1][4] = 10; G->arc[2][0] = 4; G->arc[2][5] = 5; G->arc[3][2] = 2; G->arc[3][4] = 2; G->arc[3][5] = 8; G->arc[3][6] = 4; G->arc[4][6] = 6; G->arc[6][5] = 1; } //显示邻接矩阵 void showGraph(MGraph G) { for (int i = 0; i < G.numVertexes; i++) { for (int j = 0; j < G.numVertexes; j++) { if (G.arc[i][j] != INFINITY) printf("%5d", G.arc[i][j]); else printf(" 0"); } printf("\n"); } }
void Dijkatra(MGraph G,int s) { int path[MAXVEX]; //是数组下标表示的顶点所经历的前一个顶点 int dist[MAXVEX]; //是数组下标表示的顶点的最小权值路径和 //上面两个数组都有作用,和无权最短路径一致,但是无权最短路径可以使用dist是否被设置来判断一个顶点是否被访问, //但是这里无法使用,因为dist和普里姆算法中的lowcost一样,是使用贪心算法时,每到一个顶点,我们都会全部更新dist //所以我们需要另外一个数组来标志各个顶点是否被访问 int final[MAXVEX]; int i,j,k,min; //对数据进行初始化 for (i = 0; i < G.numVertexes;i++) { final[i] = 0; //0表示该数组下标所表示的顶点未被访问 path[i] = 0; //初始化路径数组为0,表示当前每个都是独立的根节点 dist[i] = G.arc[s][i]; //这一步是重点:初始化路径数组的值为起始v0到各个点的权值 } dist[s] = 0; //到源点自己的路径为0 path[s] = s; //设置源点的前一个顶点就是自己 final[s] = 1; //源点被访问过了 //开始主循环,每次求的v0(s)到某个v顶点的最短路径 for (i = 0; i < G.numVertexes;i++) { min = INFINITY; //和普里姆算法相似 for (j = 0; j < G.numVertexes;j++) //由于是有向图所以都要从0开始,找到他的每个邻接点 { if (!final[j]&&dist[j]<min) //若是该顶点没有被访问过,且该点到s点的距离小于min,我们就将min设置为他 { k = j; //记录下该v到s点的下标和min最小路径 min = dist[j]; } } final[k] = 1; //将目前找到的距离v0(S)最近的顶点置为1 for (j = 0; j < G.numVertexes;j++) //修正当前最短路径即距离 { //修正方法就是循环k的每个邻接点,我们作为三角形来看,若是两边之和小于第三边,那我们原来找的那条直接的最短边就失效了,用这两条直接代替 //所以我们将距离修改,路径设置为他的上一步k, if (!final[j]&&(min+G.arc[k][j])<dist[j]) { //说明找到了更短的路径,修改dist和path数组 dist[j] = min + G.arc[k][j]; //修改当前路径长度 path[j] = k; } } } for (i = 0; i<G.numVertexes; i++) { printf("%d %c-%c\n", dist[i], G.vers[path[i]], G.vers[i]); } }
解释:
迪杰斯特拉算法和普里姆算法和上面的无权最短路径算法相似,前两个红线处也是重点。自己想想。
下面来看第三处
for (j = 0; j < G.numVertexes;j++) //修正当前最短路径即距离 { //修正方法就是循环k的每个邻接点,我们作为三角形来看,若是两边之和小于第三边,那我们原来找的那条直接的最短边就失效了,用这两条直接代替 //所以我们将距离修改,路径设置为他的上一步k, if (!final[j]&&(min+G.arc[k][j])<dist[j]) { //说明找到了更短的路径,修改dist和path数组 dist[j] = min + G.arc[k][j]; //修改当前路径长度 path[j] = k; } }
我们选取源点的第一次循环来讲解
1.首先:我们前面的代码已经确定了源点(0)的最短路径
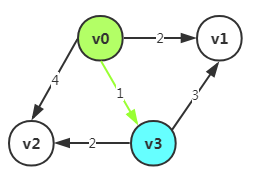
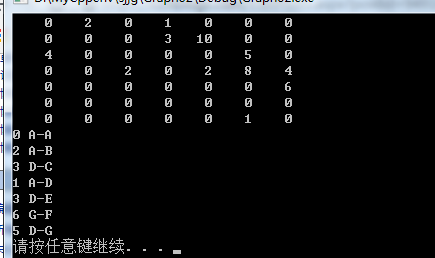
例如上图:我们确定了v0点的最短距离是v0-v3是1,所以我们将final[3]=1
2.我们在第三处,for循环中,修正的最短距离,不是我们v3距离,而是我们v3的邻接点的最短距离。
原来我们的dist是:
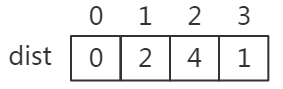
现在我们的for循环将去修正他,修正的方法是:
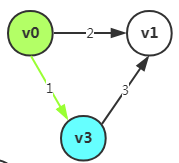
因为v1未被标记,而且min(就是d(v0-v3))+d(v3-v1)=1+3大于原来的dist[1]=2,所以不予理会

因为v2未被标记,而且min(就是d(v0-v3))+d(v3-v2)=1+2小于原来的dist[2]=4,所以我们将他的距离修改,变为dist[2]=min+E(3,2),将他的路径也做修正,他的是一个顶点变为v3,path[2]=3
修正后的dist数组是:
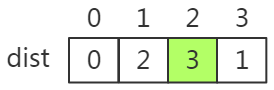
for (j = 0; j < G.numVertexes;j++) //修正当前最短路径即距离 { //修正方法就是循环k的每个邻接点,我们作为三角形来看,若是两边之和小于第三边,那我们原来找的那条直接的最短边就失效了,用这两条直接代替 //所以我们将距离修改,路径设置为他的上一步k, if (!final[j]&&(min+G.arc[k][j])<dist[j]) { //说明找到了更短的路径,修改dist和path数组 dist[j] = min + G.arc[k][j]; //修改当前路径长度 path[j] = k; } }
最后:说一句
有向图和无向图无非就是矩阵不对称而已,求最短路径几乎是一致的。所以不必考虑太多
Dijkstra算法解决了从某个顶点到其余各顶点的最短路径。其时间复杂度是O(n*2)
四:基于无向图的顶点加权Dijkstra算法

#define _CRT_SECURE_NO_WARNINGS #include <stdio.h> #include <stdlib.h> #include <stdbool.h> #define MAXVEX 100 #define INFINITY 65535 typedef char VertexType; typedef int EdgeType; typedef struct { VertexType vers[MAXVEX]; //顶点表 EdgeType arc[MAXVEX][MAXVEX]; //邻接矩阵 int numVertexes, numEdges; //图中的顶点数和边数 }MGraph; //创建邻接矩阵 void CreateMGraph(MGraph* G); //显示邻接矩阵 void showGraph(MGraph G); //迪杰斯特拉算法,获取最短路径 void Dijkatra(MGraph G, int s);

//显示邻接矩阵 void showGraph(MGraph G) { for (int i = 0; i < G.numVertexes; i++) { for (int j = 0; j < G.numVertexes; j++) printf("%6d", G.arc[i][j]); printf("\n"); } }
(一)创建拓扑图
void CreateMGraph(MGraph* G) { int i, j; G->numVertexes = 7; G->numEdges = 12; //读入顶点信息 G->vers[0] = 'A'; G->vers[1] = 'B'; G->vers[2] = 'C'; G->vers[3] = 'D'; G->vers[4] = 'E'; G->vers[5] = 'F'; G->vers[6] = 'G'; G->vers[7] = 'H'; G->vers[8] = 'I'; for (i = 0; i < G->numVertexes; i++) for (j = 0; j < G->numVertexes; j++) G->arc[i][j] = INFINITY; //邻接矩阵初始化 //创建了有向邻接矩阵 G->arc[0][1] = G->arc[1][0] = 2; G->arc[0][3] = G->arc[3][0] = 1; G->arc[1][3] = G->arc[3][1] = 3; G->arc[1][4] = G->arc[4][1] = 5; G->arc[2][0] = G->arc[0][2] = 4; G->arc[2][5] = G->arc[5][2] = 5; G->arc[3][2] = G->arc[2][3] = 2; G->arc[3][4] = G->arc[4][3] = 2; G->arc[3][5] = G->arc[5][3] = 8; G->arc[3][6] = G->arc[6][3] = 4; G->arc[4][6] = G->arc[6][4] = 2; G->arc[6][5] = G->arc[5][6] = 3;
//读入顶点信息 for (i = 0; i < G->numVertexes; i++) G->arc[i][i] = 0; G->arc[1][1] = 4; G->arc[2][2] = 2; G->arc[3][3] = 10; G->arc[4][4] = 1; G->arc[5][5] = 3; }
(二)实现基于顶点加权算法
void Dijkatra(MGraph G, int s) { int path[MAXVEX]; //是数组下标表示的顶点所经历的前一个顶点 int dist[MAXVEX]; //是数组下标表示的顶点的最小权值路径和 //上面两个数组都有作用,和无权最短路径一致,但是无权最短路径可以使用dist是否被设置来判断一个顶点是否被访问, //但是这里无法使用,因为dist和普里姆算法中的lowcost一样,是使用贪心算法时,每到一个顶点,我们都会全部更新dist //所以我们需要另外一个数组来标志各个顶点是否被访问 int final[MAXVEX]; int i, j, k, min; //对数据进行初始化 for (i = 0; i < G.numVertexes; i++) { final[i] = 0; //0表示该数组下标所表示的顶点未被访问 path[i] = 0; //初始化路径数组为0,表示当前每个都是独立的根节点 dist[i] = G.arc[s][i]; //这一步是重点:初始化路径数组的值为起始v0到各个点的权值 } dist[s] = 0; //到源点自己的路径为0 path[s] = s; //设置源点的前一个顶点就是自己 final[s] = 1; //源点被访问过了 //开始主循环,每次求的v0(s)到某个v顶点的最短路径----(找到距离源点s,并且没有被访问过的顶点的最近顶点) for (i = 0; i < G.numVertexes; i++) { min = INFINITY; //和普里姆算法相似 for (j = 0; j < G.numVertexes; j++) //由于是有向图所以都要从0开始,找到他的每个邻接点 { if (!final[j] && dist[j] < min) //若是该顶点没有被访问过,且该点到s点的距离小于min,我们就将min设置为他 { k = j; //记录下该v到s点的下标和min最小路径 min = dist[j]; } } final[k] = 1; //将目前找到的距离v0(S)最近的顶点置为1 for (j = 0; j < G.numVertexes; j++) //修正当前最短路径即距离 { //修正方法就是循环k的每个邻接点,我们作为三角形来看,若是两边之和小于第三边,那我们原来找的那条直接的最短边就失效了,用这两条直接代替 //所以我们将距离修改,路径设置为他的上一步k, if (!final[j] &&k!=j&&(min + G.arc[k][j]+G.arc[k][k]) < dist[j]) //开始加上了经过的顶点权值进行比较 { //说明找到了更短的路径,修改dist和path数组 dist[j] = min + G.arc[k][j] + G.arc[k][k]; //修改当前路径长度,是加上途经的顶点权值 path[j] = k; } } } for (i = 0; i < G.numVertexes; i++) { printf("%d %c-%c\n", dist[i], G.vers[path[i]], G.vers[i]); } }
(三)结果显示
int main() { MGraph MG; CreateMGraph(&MG); showGraph(MG); Dijkatra(MG, 0); system("pause"); return 0; }