从图的某一顶点出发访遍其余顶点,且使每一个顶点仅被访问一次,这一过程就叫做图的遍历
一:深度优先遍历(邻接矩阵实现)
(一)定义
假设给定图G的初态是所有顶点均未曾访问过。在G中任选一顶点v为初始出发点(源点),则深度优先遍历可定义如下:首先访问出发点v,并将其标记为已访问过;然后依次从v出发搜索v的每个邻接点w。若w未曾访问过,则以w为新的出发点继续进行深度优先遍历,直至图中所有和源点v有路径相通的顶点(亦称为从源点可达的顶点)均已被访问为止。若此时图中仍有未访问的顶点(未连通),则另选一个尚未访问的顶点作为新的源点重复上述过程,直至图中所有顶点均已被访问为止。
图的深度优先遍历类似于树的前序遍历。采用的搜索方法的特点是尽可能先对纵深方向进行搜索。这种搜索方法称为深度优先搜索(Depth-First Search)。相应地,用此方法遍历图就很自然地称之为图的深度优先遍历
(二)实现思路
(1)访问顶点v;
(2)从v的未被访问的邻接点中选取一个顶点w,从w出发进行深度优先遍历;
(3)重复上述两步,直至图中所有和v有路径相通的顶点都被访问到。
(三)递归实现伪代码
(1)访问顶点v;visited[v]=1;//算法执行前visited[n]=0
(2)w=顶点v的第一个邻接点;
(3)while(w存在)
if(w未被访问)
从顶点w出发递归执行该算法;
w=顶点v的下一个邻接点;
(四)非递归实现伪代码
(1)栈S初始化;visited[n]=0;
(2)访问顶点v;visited[v]=1;顶点v入栈S
(3)while(栈S非空)
x=栈S的顶元素(不出栈);
if(存在并找到未被访问的x的邻接点w)
访问w;visited[w]=1;
w进栈;
else
x出栈;
(五)代码实现(递归+非递归)
头文件


#pragma once
#ifndef _STACK_H
#define _STACK_H
#include <stdio.h>
#include <stdlib.h>
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXSIZE 100
typedef int ElemType;
typedef int Status;
typedef struct
{
ElemType data[MAXSIZE];
int top;
}Stack;
Status InitStack(Stack* S);
Status Push(Stack* S, ElemType e);
Status Pop(Stack* S, ElemType* e);
Status EmptyStack(Stack S);
ElemType getTop(Stack S);
#endif
stack.h

#pragma once
#ifndef _SEARCH_H
#define _SEARCH_H
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <stdbool.h>
#define MAXVEX 100 //最大顶点数
#define INFINITY 0 //用0表示∞
typedef char VertexType; //顶点类型,字符型A,B,C,D...
typedef int EdgeType; //边上权值类型10,15,...
typedef struct
{
VertexType vers[MAXVEX]; //顶点表
EdgeType arc[MAXVEX][MAXVEX]; //邻接矩阵,可看作边表
int numVertexes, numEdges; //图中当前的顶点数和边数
}MGraph;
#endif
01search.h源文件


#include "stack.h"
Status InitStack(Stack* S)
{
if (!S)
return ERROR;
S->top = -1;
return OK;
}
Status Push(Stack* S, ElemType e)
{
if (!S)
return ERROR;
S->data[++S->top] = e;
return OK;
}
Status Pop(Stack* S, ElemType* e)
{
if (!S || !e)
return ERROR;
*e = S->data[S->top--];
return OK;
}
Status EmptyStack(Stack S)
{
if (S.top != -1)
return FALSE;
return TRUE;
}
ElemType getTop(Stack S)
{
if (S.top == -1)
return NULL;
return S.data[S.top];
}
stack.c
#include "01search.h"
#include "stack.h"
bool visited[MAXVEX]; //访问标志的数组
void CreateMGraph(MGraph* G); //创建邻接矩阵
void DFSTraverse(MGraph M); //深度优先遍历前会进行初始化
void DFS(MGraph M, int i); //邻接矩阵深度优先算法
void DFSInter(MGraph M, int i); //邻接矩阵深度非递归优先算法
void showGraph(MGraph G); //显示矩阵


void CreateMGraph(MGraph* G)
{
int i, j, k, w;
// printf("please input number of vertex and edge:\n");
// scanf("%d,%d", &G->numVertexes, &G->numEdges); //输入顶点数和边数
// getchar(); //可以获取回车符
// for (i = 0; i < G->numVertexes; i++) //读入顶点信息,建立顶点表
// scanf("%c", &G->vers[i]);
G->numVertexes = 9;
G->numEdges = 15;
//读入顶点信息
G->vers[0] = 'A';
G->vers[1] = 'B';
G->vers[2] = 'C';
G->vers[3] = 'D';
G->vers[4] = 'E';
G->vers[5] = 'F';
G->vers[6] = 'G';
G->vers[7] = 'H';
G->vers[8] = 'I';
//getchar(); //可以获取回车符
for (i = 0; i < G->numVertexes; i++)
for (j = 0; j < G->numVertexes; j++)
G->arc[i][j] = INFINITY; //邻接矩阵初始化
G->arc[0][1] = 1;
G->arc[0][5] = 1;
G->arc[1][2] = 1;
G->arc[1][8] = 1;
G->arc[1][6] = 1;
G->arc[2][3] = 1;
G->arc[2][8] = 1;
G->arc[3][4] = 1;
G->arc[3][7] = 1;
G->arc[3][6] = 1;
G->arc[3][8] = 1;
G->arc[4][5] = 1;
G->arc[4][7] = 1;
G->arc[5][6] = 1;
G->arc[6][7] = 1;
for (k = 0; k < G->numVertexes; k++) //读入numEdges条边,建立邻接矩阵
{
for (i = k; i < G->numVertexes; i++)
{
G->arc[i][k] = G->arc[k][i]; //因为是无向图,所有是对称矩阵
}
}
}
CreateMGraph创建邻接矩阵

void showGraph(MGraph G)
{
for (int i = 0; i < G.numVertexes; i++)
{
for (int j = 0; j < G.numVertexes; j++)
printf("%2d", G.arc[i][j]);
printf("\n");
}
}
showGraph显示邻接矩阵

void DFSTraverse(MGraph M)
{
int i;
for (i = 0; i < M.numVertexes; i++)
visited[i] = false; //初始化所有顶点状态都是未访问过的未访问状态
for (i = 0; i < M.numVertexes; i++)
if (!visited[i]) //对未访问的顶点调用DFS,若是连通图,只会调用一次
DFSInter(M, i);
//DFS(M, i);
}
DFSTraverse深度优先前的初始化和调用

void DFS(MGraph M, int i) //邻接矩阵深度优先算法
{
int j;
visited[i] = true; //访问后我们会一直向后退,去访问其他结点,不会再访问这个结点,所有我们不需要再置为false
printf("%c", M.vers[i]);
for (j = 0; j < M.numVertexes; j++)
if (M.arc[i][j] == 1 && !visited[j]) //因为邻接矩阵是对称的,所以当我们访问到下半部时,有一些结点时前面已经访问过的,我们就不要重复了
DFS(M, j); //对未访问过的邻接顶点递归调用
}
DFS深度优先递归实现

void DFSInter(MGraph M, int i) //邻接矩阵深度非递归优先算法
{
int j,flag;
Stack s;
InitStack(&s);
visited[i] = true; //访问后我们会一直向后退,去访问其他结点,不会再访问这个结点,所有我们不需要再置为false
printf("%c", M.vers[i]);
Push(&s, i);
while (!EmptyStack(s))
{
i = getTop(s);
for (j = 0; j < M.numVertexes; j++)
if (M.arc[i][j] == 1 && !visited[j]) //因为邻接矩阵是对称的,所以当我们访问到下半部时,有一些结点时前面已经访问过的,我们就不要重复了
{
visited[j] = true;
printf("%c", M.vers[j]);
flag = 1;
Push(&s, j);
break;
}
if (!flag)
Pop(&s, &i);
flag = 0;
}
}
DFSInter深度优先非递归实现
int main()
{
MGraph MG;
CreateMGraph(&MG);
showGraph(MG);
DFSTraverse(MG);
system("pause");
return 0;
}
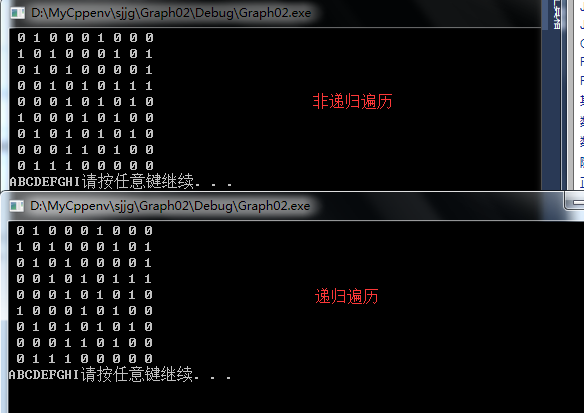
注意:深度优先遍历的方法不止一种,结果也有不同种,当我们使用方法一致时,结果是一样的,无论递归还是迭代
(六)应用:马踏棋盘
规则
8*8方格,将马放在任意位置,按照马走日,进行移动,要求一个方格进入一次,最后使得马走遍64个方格
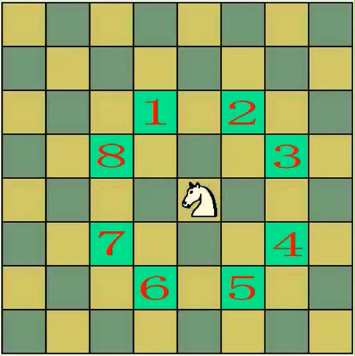
回溯法
一条路走到黑,碰壁了再回来一条路走。可以与递归很好搭配,也可以和深度优先搜索一起
哈密尔顿路径
是指结果图G中的每个顶点,且只经过一次的一条轨迹。如果这条轨迹是一个闭合的路径(从起点出发不重复的遍历所有点后仍能回到起始点),那么这条路径叫做哈密尔顿回路
代码实现


#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define X 8
#define Y 8
int chess[X][Y];
//找到x,y位置的下一个可走位置,并返回,其中count代表了我们尝试了多少次,一个有八种走法,所有count从0-7
//按照棋盘显示的来走
int nextxy(int* x, int* y, int count)
{
switch (count)
{
case 0:
if ((*x + 2) < X && (*y - 1) >= 0 && !chess[*x + 2][*y - 1])
{
*x += 2;
*y -= 1;
return 1;
}
break;
case 1:
if ((*x + 2) < X && (*y + 1) < Y && !chess[*x + 2][*y + 1])
{
*x += 2;
*y += 1;
return 1;
}
break;
case 2:
if ((*x + 1) < X && (*y - 2) >= 0 && !chess[*x + 1][*y - 2])
{
*x += 1;
*y -= 2;
return 1;
}
break;
case 3:
if ((*x + 1) < X && (*y + 2) < Y && !chess[*x + 1][*y + 2])
{
*x += 1;
*y += 2;
return 1;
}
break;
case 4:
if ((*x - 2) >= 0 && (*y - 1) >= 0 && !chess[*x - 2][*y - 1])
{
*x -= 2;
*y -= 1;
return 1;
}
break;
case 5:
if ((*x - 2) >= 0 && (*y + 1) < Y && !chess[*x - 2][*y + 1])
{
*x -= 2;
*y += 1;
return 1;
}
break;
case 6:
if ((*x - 1) >= 0 && (*y - 2) >= 0 && !chess[*x - 1][*y - 2])
{
*x -= 1;
*y -= 2;
return 1;
}
break;
case 7:
if ((*x - 1) >= 0 && (*y + 2) < Y && !chess[*x - 1][*y + 2])
{
*x -= 1;
*y += 2;
return 1;
}
break;
default:
break;
}
return 0;
}
void ShowChess()
{
for (int i = 0; i < X;i++)
{
for (int j = 0; j < Y;j++)
{
printf("%5d", chess[i][j]);
}
printf("\n");
}
}
//深度优先遍历棋盘
//(x,y)为位置坐标
//第一次调用为我们输入的参数
//之后就是递归进行
//tag代表我们在棋盘上走的正确步数
TravelChessBoard(int x, int y, int tag)
{
int flag,count=0;
int x1, y1;
x1 = x;
y1 = y;
chess[x][y] = tag;
if (tag==X*Y)
{
//打印棋盘
ShowChess();
return 1;
}
flag = nextxy(&x1, &y1, count); //我们只找了其中一种走法,如果没有找到,我们下面需要去遍历其他走法
while (++count < 8 && !flag)
{
flag = nextxy(&x1, &y1, count);
}
//找到路径了
while (flag) //我们对这个点周围的所有可以走的位置都要遍历一下
{
if (TravelChessBoard(x1, y1, tag + 1))
return 1;
//若是这条路走不通,我们需要继续换下一条路,上面的count代表我们走到第几条路
x1 = x;
y1 = y;
flag = nextxy(&x1, &y1, count);
while (++count < 8 && !flag)
{
flag = nextxy(&x1, &y1, count);
}
}
//如果这个点各个方向都不行,我们就要换点了,先将这个点置为0
if (0 == flag)
{
chess[x][y] = 0; //因为这里要用到原来x,y,所以我们需要保留他
}
return 0;
}
int main()
{
clock_t start, end;
int i, j;
start = clock();
for (i = 0; i < X; i++)
for (j = 0; j < Y; j++)
chess[i][j] = 0;
if (!TravelChessBoard(2, 0, 1))
printf("find ways failure!\n");
end = clock();
printf("time speed:%f(ms)\n", (double)(end - start)/CLOCKS_PER_SEC);
system("pause");
return 0;
}
View Code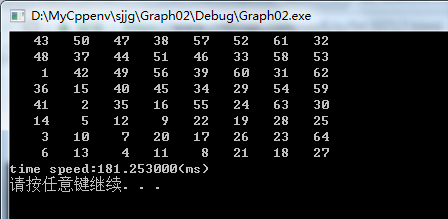
二:广度优先遍历(邻接矩阵)
(一)定义
图的广度优先遍历BFS算法是一个分层搜索的过程,和树的层序遍历算法类同,它也需要一个队列以保持遍历过的顶点顺序,以便按出队的顺序再去访问这些顶点的邻接顶点。
(二)实现思路
(1)顶点v入队列。
(2)当队列非空时则继续执行,否则算法结束。
(3)出队列取得队头顶点v;访问顶点v并标记顶点v已被访问。
(4)查找顶点v的第一个邻接顶点col。
(5)若v的邻接顶点col未被访问过的,则col入队列。
(6)继续查找顶点v的另一个新的邻接顶点col,转到步骤(5)。
直到顶点v的所有未被访问过的邻接点处理完。转到步骤(2)。
广度优先遍历图是以顶点v为起始点,由近至远,依次访问和v有路径相通而且路径长度为1,2,……的顶点。为了使“先被访问顶点的邻接点”先于“后被访问顶点的邻接点”被访问,需设置队列存储访问的顶点。
(三)伪代码
(1)初始化队列Q;visited[n]=0;
(2)访问顶点v;visited[v]=1;顶点v入队列Q;
(3) while(队列Q非空)
v=队列Q的对头元素出队;
w=顶点v的第一个邻接点;
while(w存在)
如果w未访问,则访问顶点w;
visited[w]=1;
顶点w入队列Q;
w=顶点v的下一个邻接点。
(四)代码实现


#pragma once
#ifndef _QUEUE_H
#define _QUEUE_H
#include <stdio.h>
#include <stdlib.h>
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXSIZE 100
typedef int ElemType;
typedef int Status;
typedef struct _qNode
{
ElemType data;
struct _qNode* next;
}QNode,*QNodePtr;
typedef struct
{
QNodePtr front,rear; //队头队尾指针
}LinkQueue;
Status InitQueue(LinkQueue* Q);
Status EnQueue(LinkQueue* Q, ElemType e);
Status DeQueue(LinkQueue* Q, ElemType* e);
Status EmptyQueue(LinkQueue Q);
Status getHead(LinkQueue Q,ElemType* e);
#endif
queue.h

#include "queue.h"
Status InitQueue(LinkQueue* Q)
{
if (!Q)
return ERROR;
Q->front = Q->rear = (QNodePtr)malloc(sizeof(QNode));
if (!Q->front)
return ERROR;
Q->front->next = NULL;
return OK;
}
Status EnQueue(LinkQueue* Q, ElemType e)
{
//尾插法
if (!Q)
return ERROR;
QNodePtr q = (QNodePtr)malloc(sizeof(QNode));
if (!q)
return ERROR;
q->data = e;
q->next = (*Q).rear->next;
(*Q).rear->next = q;
Q->rear = q;
return OK;
}
Status DeQueue(LinkQueue* Q, ElemType* e)
{
QNodePtr q;
if (!Q || !e || EmptyQueue(*Q))
return ERROR;
q = Q->front->next;
Q->front->next = q->next;
*e = q->data;
if (Q->rear == q)
Q->rear = Q->front;
free(q);
return OK;
}
Status EmptyQueue(LinkQueue Q)
{
if (!Q.front->next)
return TRUE;
return FALSE;
}
Status getHead(LinkQueue Q,ElemType* e)
{
QNodePtr q;
if (EmptyQueue(Q))
return ERROR;
q = Q.front->next;
*e = q->data;
return OK;
}
queue.c

void BFSTraverse(MGraph G)
{
LinkQueue Q;
int i,j,k;
for (i = 0; i < G.numVertexes; i++)
visited[i] = false; //初始化所有顶点状态都是未访问过的未访问状态
InitQueue(&Q);
for (i = 0; i < G.numVertexes;i++)
{
if (!visited[i]) //若是未访问过的就处理
{
visited[i] = true; //设置当前顶点被访问过了
printf("%c", G.vers[i]); //打印顶点
EnQueue(&Q, i); //将此顶点入队
while (!EmptyQueue(Q)) //若当前顶点不为空
{
DeQueue(&Q, &k); //出队,获取出队行的相关列
for (j = 0; j < G.numVertexes;j++)
{
if (G.arc[k][j]==1&&!visited[j]) //若是该列未被访问
{
visited[j] = true; //标记访问过
printf("%c", G.vers[j]); //输出数据
EnQueue(&Q, j); //将其入队
}
}
}
}
}
}
void BFSTraverse(MGraph G)广度优先实现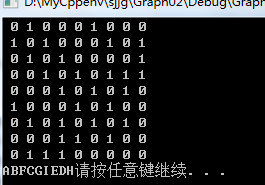
三:邻接表实现深度优先和广度优先
队列和栈的实现代码如上面一致


#pragma once
#ifndef _SEARCH_H
#define _SEARCH_H
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <stdbool.h>
#define MAXVEX 100 //最大顶点数
#define INFINITY 0 //用0表示∞
typedef char VertexType; //顶点类型,字符型A,B,C,D...
typedef int EdgeType; //边上权值类型10,15,...
//邻接矩阵结构
typedef struct
{
VertexType vers[MAXVEX]; //顶点表
EdgeType arc[MAXVEX][MAXVEX]; //邻接矩阵,可看作边表
int numVertexes, numEdges; //图中当前的顶点数和边数
}MGraph;
//邻接表结构
//边表结点
typedef struct _EdgeNode
{
int adjvex; //存放邻接点
struct _EdgeNode* next; //指向下一个
}EdgeNode;
//顶点表结点
typedef struct _VertexNode
{
VertexType data; //顶点域,存储顶点信息
EdgeNode* fisrtedge; //边表头指针
}VertexNode, AdjList[MAXVEX];
//邻接表指针
typedef struct
{
AdjList adjList; //邻接表数组
int numVertexes, numEdges; //图中所存储的顶点数和边表数
}GraphAdjList;
#endif
01search.h
#include "01search.h"
#include "stack.h"
#include "queue.h"
bool visited[MAXVEX]; //访问标志的数组
void CreateMGraph(MGraph* G);
void CreateALGraph(MGraph G, GraphAdjList *GL);//利用邻接矩阵构建邻接表
void DFSTraverse(GraphAdjList M);
void DFS(GraphAdjList G, int i); //邻接矩阵深度优先算法
void DFSInter(GraphAdjList G, int i); //邻接矩阵深度非递归优先算法
void BFSTraverse(GraphAdjList G); //广度优先遍历
void showGraph(MGraph G); //显示邻接矩阵
void ShowGraphAdjList(GraphAdjList GL); //显示邻接表
int main()
{
MGraph MG;
GraphAdjList GL;
CreateMGraph(&MG);
showGraph(MG);
CreateALGraph(MG, &GL);
ShowGraphAdjList(GL);
DFSTraverse(GL);
BFSTraverse(GL);
system("pause");
return 0;
}
void CreateMGraph(MGraph* G)
{
int i, j, k, w;
// printf("please input number of vertex and edge:\n");
// scanf("%d,%d", &G->numVertexes, &G->numEdges); //输入顶点数和边数
// getchar(); //可以获取回车符
// for (i = 0; i < G->numVertexes; i++) //读入顶点信息,建立顶点表
// scanf("%c", &G->vers[i]);
G->numVertexes = 9;
G->numEdges = 15;
//读入顶点信息
G->vers[0] = 'A';
G->vers[1] = 'B';
G->vers[2] = 'C';
G->vers[3] = 'D';
G->vers[4] = 'E';
G->vers[5] = 'F';
G->vers[6] = 'G';
G->vers[7] = 'H';
G->vers[8] = 'I';
//getchar(); //可以获取回车符
for (i = 0; i < G->numVertexes; i++)
for (j = 0; j < G->numVertexes; j++)
G->arc[i][j] = INFINITY; //邻接矩阵初始化
G->arc[0][1] = 1;
G->arc[0][5] = 1;
G->arc[1][2] = 1;
G->arc[1][8] = 1;
G->arc[1][6] = 1;
G->arc[2][3] = 1;
G->arc[2][8] = 1;
G->arc[3][4] = 1;
G->arc[3][7] = 1;
G->arc[3][6] = 1;
G->arc[3][8] = 1;
G->arc[4][5] = 1;
G->arc[4][7] = 1;
G->arc[5][6] = 1;
G->arc[6][7] = 1;
for (k = 0; k < G->numVertexes; k++) //读入numEdges条边,建立邻接矩阵
{
for (i = k; i < G->numVertexes; i++)
{
G->arc[i][k] = G->arc[k][i]; //因为是无向图,所有是对称矩阵
}
}
}
//利用邻接矩阵构建邻接表
void CreateALGraph(MGraph G, GraphAdjList *GL)
{
EdgeNode* e;
int i,j;
//设置顶点数和边表数
GL->numEdges = G.numEdges;
GL->numVertexes = G.numVertexes;
//建立顶点表
for (i = 0; i < G.numVertexes;i++)
{
GL->adjList[i].data = G.vers[i];
GL->adjList[i].fisrtedge = NULL;
}
//建立边表
for (i = 0; i < G.numVertexes;i++)
{
for (j = 0; j < G.numVertexes;j++)
{
if (G.arc[i][j]==1)
{
e = (EdgeNode*)malloc(sizeof(EdgeNode));
e->adjvex = j;
e->next = GL->adjList[i].fisrtedge;
GL->adjList[i].fisrtedge = e;
}
}
}
}
void DFSTraverse(GraphAdjList G)
{
int i;
for (i = 0; i < G.numVertexes; i++)
visited[i] = false; //初始化所有顶点状态都是未访问过的未访问状态
for (i = 0; i < G.numVertexes; i++)
if (!visited[i]) //对未访问的顶点调用DFS,若是连通图,只会调用一次
//DFSInter(G, i);
DFS(G, i);
printf("\n");
}
void DFS(GraphAdjList G, int i) //邻接矩阵深度优先算法
{
int j;
EdgeNode* p;
visited[i] = true; //访问后我们会一直向后退,去访问其他结点,不会再访问这个结点,所有我们不需要再置为false
printf("%c", G.adjList[i].data); //打印顶点
p = G.adjList[i].fisrtedge;
while (p)
{
if (!visited[p->adjvex])
DFS(G, p->adjvex);
p = p->next;
}
}
void DFSInter(GraphAdjList G, int i) //邻接矩阵深度非递归优先算法
{
int j, flag;
Stack s;
EdgeNode* e;
InitStack(&s);
visited[i] = true; //访问后我们会一直向后退,去访问其他结点,不会再访问这个结点,所有我们不需要再置为false
printf("%c", G.adjList[i].data);
Push(&s, i);
while (!EmptyStack(s))
{
i = getTop(s);
e = G.adjList[i].fisrtedge;
while (e)
{
if (!visited[e->adjvex])
{
printf("%c", G.adjList[e->adjvex].data);
visited[e->adjvex] = true;
flag = 1;
Push(&s, e->adjvex);
break;
}
e = e->next;
}
if (!flag)
Pop(&s, &i);
flag = 0;
}
}
void BFSTraverse(GraphAdjList G)
{
LinkQueue Q;
int i, j, k;
EdgeNode* q;
for (i = 0; i < G.numVertexes; i++)
visited[i] = false; //初始化所有顶点状态都是未访问过的未访问状态
InitQueue(&Q);
for (i = 0; i < G.numVertexes; i++)
{
if (!visited[i]) //若是未访问过的就处理
{
visited[i] = true; //设置当前顶点被访问过了
printf("%c", G.adjList[i].data); //打印顶点
EnQueue(&Q, i); //将此顶点入队
while (!EmptyQueue(Q)) //若当前顶点不为空
{
DeQueue(&Q, &k); //出队,获取出队行的相关列
q = G.adjList[k].fisrtedge;
while (q)
{
if (!visited[q->adjvex])
{
visited[q->adjvex] = true; //标记访问过
printf("%c", G.adjList[q->adjvex].data); //输出数据
EnQueue(&Q, q->adjvex); //将其入队
}
q = q->next;
}
}
}
}
printf("\n");
}
void showGraph(MGraph G)
{
for (int i = 0; i < G.numVertexes; i++)
{
for (int j = 0; j < G.numVertexes; j++)
printf("%2d", G.arc[i][j]);
printf("\n");
}
}
void ShowGraphAdjList(GraphAdjList GL)
{
EdgeNode* e;
for (int i = 0; i < GL.numVertexes;i++)
{
printf("%d: ", i);
e = GL.adjList[i].fisrtedge;
while (e)
{
printf("%5d", e->adjvex);
e = e->next;
}
printf("\n");
}
}




















