数据结构（五）图---图的存储结构5种

一：图的抽象数据类型

ADT 图(Graph)

Data
    顶点的有穷非空集合和边的集合

Operation
    CreateGraph(*G,V,VR)：按照顶点集V和边弧集VR的定义构造图G
    DestroyGraph(*G)：图G存在则销毁
    LocateVex(G,u)：若图G中存在顶点u,则返回图中位置
    GetVex(G,v)：返回图中顶点v的值
    PutVex(G,v,value)：将图G中顶点v赋值给value
    FirstAdjVex(G,*v)：返回顶点v的一个邻接顶点，若顶点在G中无邻接顶点则返回空
    NextAdjVex(G,v,*w)：返回顶点v相对于顶点w的下一个邻接顶点，若w是v的最后一个邻接点则返回空
    InsertVex(*G,v)：在图G中增加新顶点v
    DeleteVex(*G,v)：删除图G中顶点v及其相关的弧
    InsertArc(*G,v,w)：在图G中添加弧<v,w>,若G是无向图，还需要添加对称弧<w,v>
    DeleteArc(*G,v,w)：在图G中删除弧<v,w>,若G是无向图，则需要删除对称弧<w,v>
    DFSTraverse(G)：对图G中进行深度优先遍历，在遍历过程对每个顶点调用
    HFSTraverse(G)：对图G中进行广度优先遍历，在遍历过程对每个顶点调用
endADT

二：图的存储结构讨论

对于线性表来说，是一对一的关系，所以用数组或者链表均可以简单存放。
对于树结构是一对多的关系，所以我们要将数组和链表的特性结合在一起才能更好的存放。
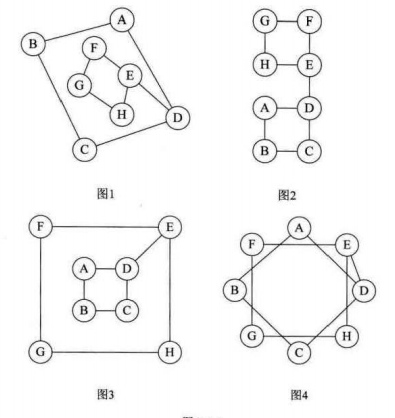
对于图来说，是多对多的情况，另外图上的任意一个顶点都可以被看做是第一个顶点，任一顶点的邻接点之间也不存在次序关系

如下图：实际是一个图结构，只不过顶点位置不同。

由于图的结构复杂，任意两个顶点之间都可能存在联系，因此无法以数据元素在内存中的物理位置来表示元素之间的关系，也就是说，图不可能用简单的顺序存储结构来表示。
内存物理位置是线性的，图的元素关系是平面的。

虽然我们可以向树结构中说到的那样使用多重链表，但是我们需要先确定最大的度，然后按照这个度最大的顶点设计结点结构，若是每个顶点的度数相差较大，就会造成大量的存储单元浪费。

三：图的存储结构（1）---邻接矩阵

考虑到图是由顶点和边（弧）两部分组成的，合在一起是比较困难的，那就很自然的考虑到分为两个结构来分别存储

顶点因为不区分大小，主次，所以用一个一维数组来存储时不错的选择。
而边或弧由于是顶点与顶点之间的关系，所以我们最好使用二维数组来存储

图的邻接矩阵存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息，一个二维数组（称为邻接矩阵）存储图中的边或弧的信息。

（一）无向图

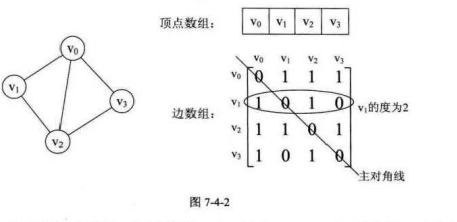
其中1表示两个顶点之间存在关系，0表示无关，不存在顶点间的边。

对称矩阵：就是n阶矩阵满足a[i][j]=a[j][i](0<=i,j<=n）。即从矩阵的左上角到右下角的主对角线为轴，右上角的源与左下角相对应的元都是相等的。

根据这个矩阵，我们可以很容易的知道图中的信息。
1.我们要判定容易两顶点是否有边无边就非常容易了。
2.我们要知道某个顶点的度，其实就是这个顶点vi在邻接矩阵中第i行（或第i列）的元素之和。比如上图顶点v1的度就是1+0+1+0=2
3.求顶点vi的所有邻接点就是将矩阵第i行元素扫描一遍，arc[i][j]为1就是邻接点

（二）有向图

对于上面的无向图，二维对称矩阵似乎浪费了一半的空间。若是存放有向图，会更大程度利用起来空间

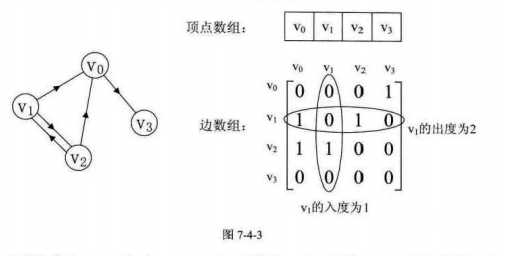
其中顶点数组是一样的和无向图，弧数组也是一个矩阵，但因为是有向图，所以这个矩阵并不对称：例如v1->v0有弧，arc[1][0]=1,而v0到v1没有弧，所以arc[0][1]=0。
另外有向图，要考虑入度和出度，顶点v1的入度为1，正好是第v1列的各数之和，顶点v1的出度为2，正好是第v2行的各数之和

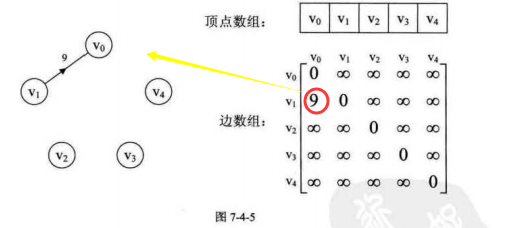
（三）网

每条边上带有权的图就叫做网

这里‘∞’表示一个计算机允许的，大于所有边上权值的值

（四）实现无向网图创建

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define MAXVEX 100    //最大顶点数
#define INFINITY 65535    //用65535表示∞

typedef char VertexType;    //顶点类型，字符型A,B,C,D...
typedef int EdgeType;    //边上权值类型10,15,...

typedef struct
{
    VertexType vers[MAXVEX];    //顶点表
    EdgeType arc[MAXVEX][MAXVEX];    //邻接矩阵，可看作边表
    int numVertexes, numEdges;    //图中当前的顶点数和边数
}MGraph;

void CreateMGraph(MGraph* G)
{
    int i, j, k, w;
    printf("please input number of vertex and edge:\n");
    scanf("%d,%d", &G->numVertexes, &G->numEdges);    //输入顶点数和边数
    getchar();    //可以获取回车符
    for (i = 0; i < G->numVertexes; i++)    //读入顶点信息，建立顶点表
        scanf("%c", &G->vers[i]);
    getchar();    //可以获取回车符
    for (i = 0; i < G->numVertexes;i++)
        for (j = 0; j < G->numVertexes;j++)
            G->arc[i][j] = INFINITY;    //邻接矩阵初始化

    for (k = 0; k < G->numEdges;k++)    //读入numEdges条边，建立邻接矩阵
    {
        printf("input edge(vi,vj) row(i),col(j),weight(w):\n");
        scanf("%d,%d,%d", &i, &j, &w);    //输入边(vi,vj),以及上面的权值
        getchar();    //可以获取回车符
        G->arc[i][j] = w;
        G->arc[j][i] = G->arc[i][j];    //因为是无向图，所有是对称矩阵
    }
}

int main()
{
    MGraph MG;
    CreateMGraph(&MG);

    system("pause");
    return 0;
}

n个顶点，e条边创建无向网图，时间复杂度是O(n+n^2+e),初始化时耗费了O(n^2)

 

四：图的存储结构（2）---邻接表

上面的邻接矩阵是一种不错的图存储结构，便于理解，但是当我们的边数相对于顶点较少的图，这种结构是存在对存储空间的极大的浪费。

我们可以考虑使用链表来动态分配空间，避免使用数组一次分配而造成空间浪费问题。

同树中，孩子表示法，我们将结点存放入数组，对结点的孩子进行链式存储，不管有多少孩子，都不会存在空间浪费。这种思路也适用于图的存储。我们把这种数组与链表相结合的存储方法称为邻接表

邻接表处理办法

1.图中顶点用一个一维数组。当然，顶点也可以用单链表来存储，不过数组可以较容易的读取顶点信息，更加方便。另外，对于顶点数组中，每个数据元素还需要存储指向第一个邻接点的指针，以便于查找该顶点的边信息

2.图中每个顶点vi的所有邻接点构成一个线性表，由于邻接点的个数不定，所以用单链表存储，无向图称为顶点vi的边表，有向图则称为顶点vi作为弧尾的出边表

（一）无向图

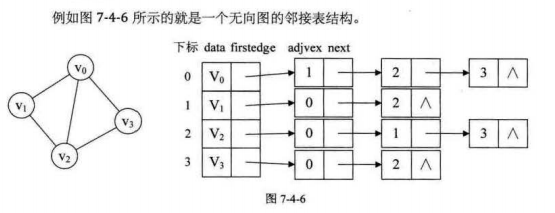
这样的结构，对于我们要获得图的相关信息也是很方便。比如：
我们要获取某个顶点的度，就要去查找这个顶点的边表中结点的个数。
我们要判断vi到vj是否存在边，只需要测试vi的边表链表中是否存在结点vj的下标j即可。
我们若是要获取顶点的所有邻接点，就是对此顶点的边表进行遍历。

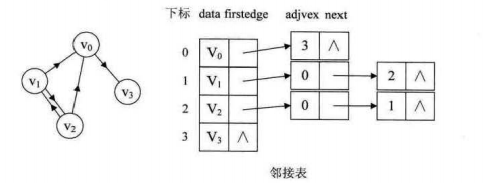
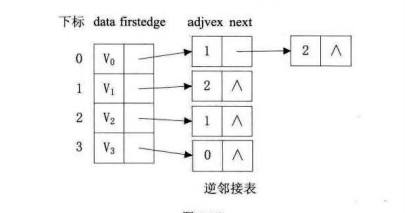
（二）有向图

有向图由于有方向，我们是以顶点为弧尾来存储边表的，这样很容易就可以得到每个顶点的出度。但是由于有时也需要确定顶点的入度或以顶点作为弧头的弧，我们可以建立一个有向图的逆邻接表，即对每个顶点vi都建立一个链接为vi为弧头的表

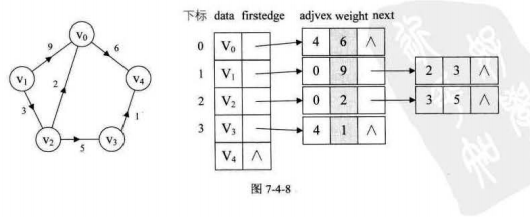
（三）带权值的网图

我们可以在边表结点定义中再增加一个weight数据域，存储权值信息即可

（四）实现无向网图

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define MAXVEX 100    //最大顶点数

typedef char VertexType;    //顶点类型，字符型A,B,C,D...
typedef int EdgeType;    //边上权值类型10,15,...

typedef struct EdgeNode    //边表结点
{
    int adjvex;            //邻接点域，存放该顶点对应的下标
    int weight;            //用于存放权值，对于非网图可以不需要
    struct EdgeNode* next;    //链域，指向下一个邻接点
}EdgeNode;

typedef struct VertexNode   //顶点表结点
{
    VertexType data;    //顶点域，存储顶点信息
    EdgeNode* firstedge;    //边表头指针
}VertexNode,AdjList[MAXVEX];

typedef struct
{
    AdjList adjList;    //邻接表数组
    int numVertexes, numEdges;    //图中所存储的顶点数和边数
}GraphAdjList;

void CreateALGraph(GraphAdjList* G)
{
    int i, j ,k,w;
    EdgeNode *e;
    printf("please input number of vertex and edge:\n");
    scanf("%d,%d",&G->numVertexes,&G->numEdges);    //输入顶点数和边数
    getchar();    //可以获取回车符
    for (i = 0; i < G->numVertexes;i++)    //输入顶点信息
    {
        scanf("%c", &G->adjList[i].data);    //输入顶点信息
        G->adjList[i].firstedge = NULL;    //将边表置为空
    }
    getchar();    //可以获取回车符
    for (k = 0; k < G->numEdges;k++)
    {
        printf("input edge(vi,vj) vertexs series and the weight:\n");
        scanf("%d,%d,%d", &i, &j,&w);
        getchar();
        //由于是无向图，对称矩阵，当我们设置边以后，需要在两个地方设置结点
        e = (EdgeNode *)malloc(sizeof(EdgeNode));
        //使用头插法将数据插入（主要是头插法方便），我们插入不需要考虑顺序，因为链表结点都是与数组顶点相连接的
        e->adjvex = j;
        e->next = G->adjList[i].firstedge;    
        e->weight = w;
        G->adjList[i].firstedge = e;

        e = (EdgeNode*)malloc(sizeof(EdgeNode));
        e->adjvex = i;
        e->next = G->adjList[j].firstedge;
        e->weight = w;
        G->adjList[j].firstedge = e;
    }
}

int main()
{
    GraphAdjList gl;
    CreateALGraph(&gl);
    system("pause");
    return 0;
}

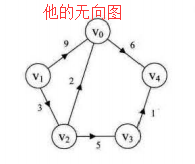
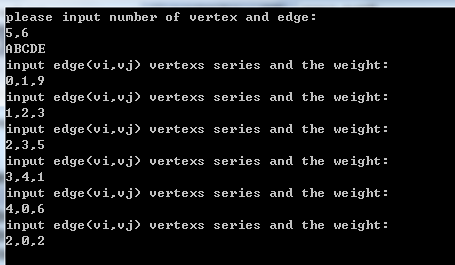
注意：上面的两种存储结构是针对顶点，下面的三种存储结构是针对边

五：图的存储结构（3）---十字链表

我们想要知道出度方向的顶点，可以使用邻接表，我们要了解入度就需要使用逆邻接表。但是我们既想要了解入度有想要了解出度，那么我们该如何处理？
这时就需要使用到有向图的一种存储方法：十字链表

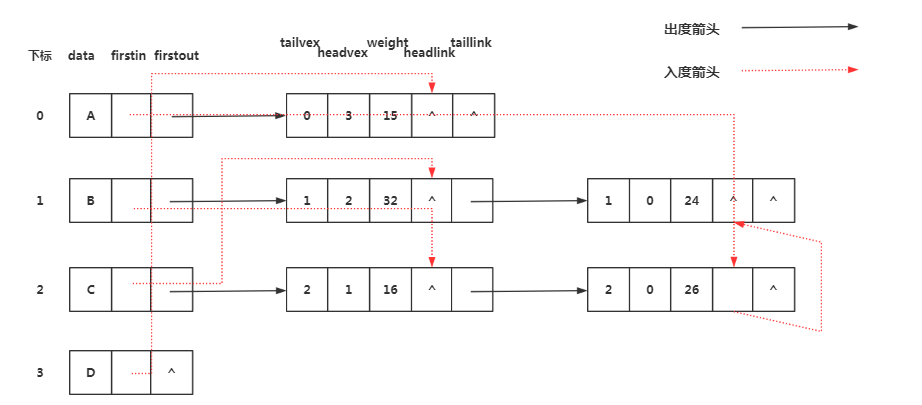
顶点表结点结构

firstin表示入边表头指针，指向该顶点的入边表中第一个结点。
firstout表示出边表头指针，指向该顶点的出边表中第一个结点。

边表结点结构

其中tailvex是指弧起点在顶点表的下标，headvex是指弧终点在顶点表的下标。
headlink是指入边表指针域，指向终点相同的下一条边，taillink是指边表指针域，指向起点相同的下一条边。
如果是网，我们还要在其中加入权值域，来存储权值

我们可以看做横向是出度，竖向是入度

顶点的出度和入度。除了结构复杂一点外，其实创建图算法的时间复杂度和邻接表是相同的，因此很好的应用在有向图中。

注意：整张图的出度和入度是一致的（不是某个顶点，而是这张图）

代码实现

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define MAXVEX 100    //最大顶点数

typedef char VertexType;    //顶点类型，字符型A,B,C,D...
typedef int EdgeType;    //边上权值类型10,15,...

typedef struct OLNode    //十字链表结点
{
    int tailvex, headvex;    //表示两个顶点下标，构成了一条边。tailvex是箭头尾，弧尾，headvex是箭头头，是弧头
    int weight;            //用于存放权值，对于非网图可以不需要
    struct OLNode* taillink;    //十字链域，指向下一个邻接点，是出度方向
    struct OLNode* headlink;    //十字链域，指向下一个邻接点，是入度方向
}OLNode;

typedef struct VertexNode   //顶点表结点
{
    VertexType data;    //顶点域，存储顶点信息
    OLNode* firstin;    //边表头指针,入度
    OLNode* firstout;    //边表头指针,出度
}VertexNode, CrossList[MAXVEX];

typedef struct
{
    CrossList adjList;    //邻接表数组
    int numVertexes, numEdges;    //图中所存储的顶点数和边数（出度指针和入度指针是和边数是一致的）
}GraphCrossList;

void CreateCrossGraph(GraphCrossList* G)
{
    int i, j ,k,w;
    OLNode *e;
    printf("please input number of vertex and edge:\n");
    scanf("%d,%d",&G->numVertexes,&G->numEdges);    //输入顶点数和边数
    getchar();    //可以获取回车符
    for (i = 0; i < G->numVertexes;i++)    //输入顶点信息
    {
        scanf("%c", &G->adjList[i].data);    //输入顶点信息
        G->adjList[i].firstin = NULL;    //将边表置为空
        G->adjList[i].firstout = NULL;    //将边表置为空
    }
    getchar();    //可以获取回车符

    //先循环获取出度结点，出度数和入度数是一致的
    for (k = 0; k < G->numEdges;k++)
    {
        printf("Out-->input edge(vi,vj) vertexs series and the weight:\n");
        scanf("%d,%d,%d", &i, &j,&w);
        getchar();
        //创建十字链表结点
        e = (OLNode *)malloc(sizeof(OLNode));
        //使用头插法将数据插入（主要是头插法方便），我们插入不需要考虑顺序，因为链表结点都是与数组顶点相连接的
        e->tailvex = i;
        e->headvex = j;
        e->weight = w;
        e->taillink = G->adjList[i].firstout;
        G->adjList[i].firstout = e;
    }

    //再循环获取入度结点，在上面的出度结点建立了所有结点的基础上，我们再建立入度指针指向
    //例如我们要获取v0的入度v1，我们先输入入度点0，再输入出度点1,不需要权值，权值在上面对有向图都赋值了
    //我们进行第二个指针v0的入度v2,我们使用相同输入，但是开始使用头插法修改链表firstin指向
    for (k = 0; k < G->numEdges; k++)
    {
        printf("In-->input edge(vi,vj) vertexs series:\n");
        scanf("%d,%d", &i, &j);
        getchar();
        //根据上面的输入，我们将当前的顶点域firstin指向我们获取的新的入度域
        //先找入度域
        e = G->adjList[j].firstout;
        while (e->headvex!=i)
            e = e->taillink;    //循环十字链表结点，获取我们要的入度结点
        //使用头插法插入入度指针域
        e->headlink = G->adjList[i].firstin;
        G->adjList[i].firstin = e;
    }
}

int main()
{
    GraphCrossList gl;
    CreateCrossGraph(&gl);
    gl;
    system("pause");
    return 0;
}

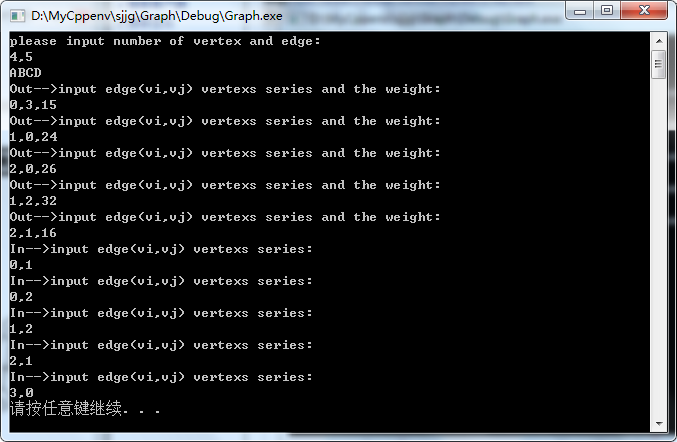
六：图的存储结构（4）---邻接多重表

邻接多重表是对无向图的存储结构的优化

问题：

对于无向图的邻接表，我们更加关注的重点是顶点，那么是不错的选择，但是我们要是关注的是边的操作。
比如：删除一条边，那么我们的操作将变得复杂，我们需要找到这条边的两个顶点，方便去其链表中删除所表示的边。稍微有点麻烦。

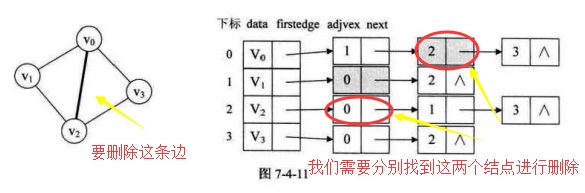
改进：

 

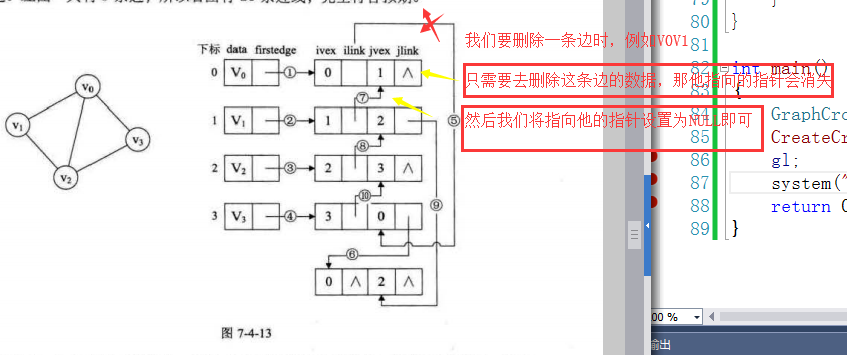
我们只出现无向图中对应条数的边表结点，其他的结构，我们全部由指针来联系，所以当我们想要删除一条边时，就只需要删除对应的边表结点。指向她的指针会置为空，他自己产生的指针会消失。就完成了对边的操作。

例如上图，我们若是使用邻接表：是要10个顶点结点去表示5条边，而我们若是使用邻接多重表，只需要5个边结点即可。删除一条边就不存在重复操作

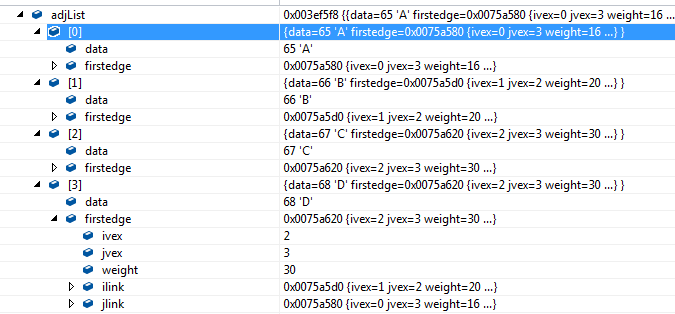
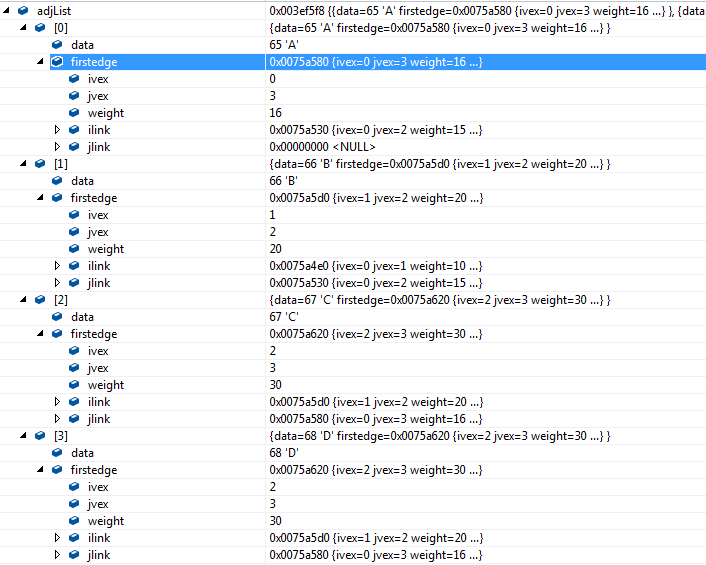
定义

邻接多重表结构

其中ivex和jvex是指某条边依附的两个顶点在顶点表中的下标。ilink指向依附顶点ivex的下一条边，jlink指向依附顶点jvex的下一条边。

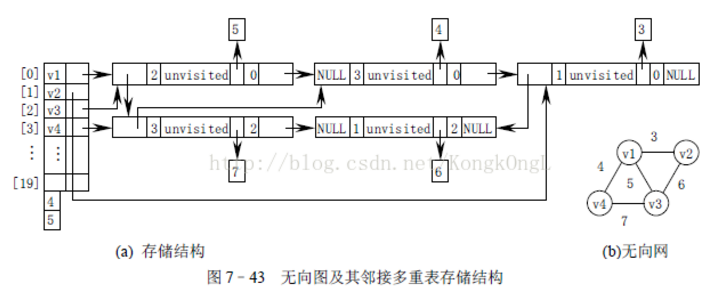
如上图有4个顶点和5条边，先将边表结点画出来。由于是无向图，所以ivex，jvex正反过来都可以，为了绘图方便，都将ivex值设置的与一旁的顶点下标相同

1.将边表结点画出来

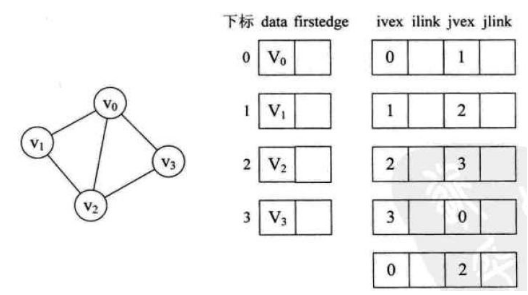
2.开始连线

首先连线的（1）（2）（3）（4）是将顶点的firstedge指向一条边，顶点下标要与ivex的值相同。

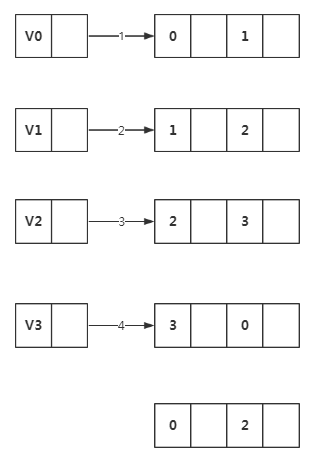
接着，由于顶点v0的(v0,v1)边的邻边有(v0,v3)和(v0,v2)。因此（5）（6）的连线就是满足指向下一条依附于顶点v0的边的目标，注意ilink指向的结点的jvex（ivex）一定要与它本身的ivex的值相同。

注意ilink指向的结点的jvex（ivex）一定要与它本身的ivex的值相同。而且为了方便，我们和jvex相同，那么全部指向都要与之一样

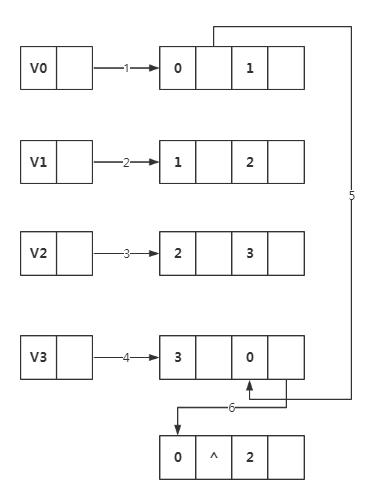
同理，连线（7）就是指（v1,v0）这条边，它是相当于顶点v1指向（v1,v2）边后的下一条。

v2有三条边依附，所以（3）之后就有了（8）（9）。

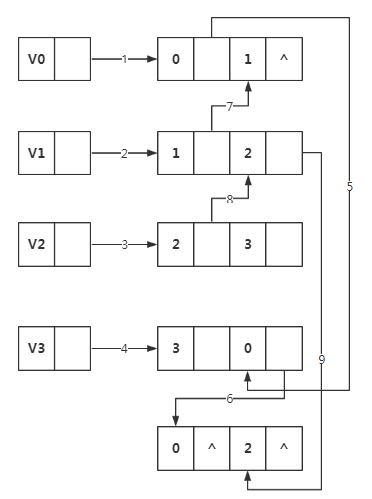
连线（10）就是顶点v3在连线（4）之后的下一条边

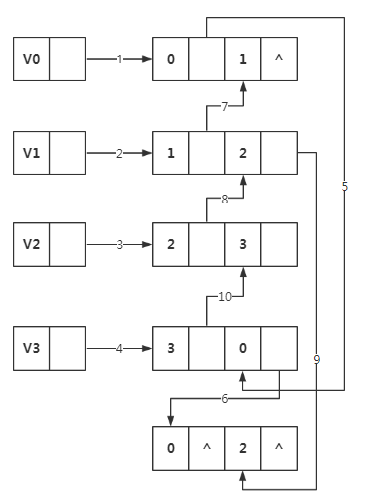
左图一共有5条边，所以右图有10条连线，完全符合预期。

总结

邻接多重表与邻接表的差别，仅仅是在于同一条边在邻接表中用两个边表结点表示，而在邻接多重表中只有一个结点。这样对边的操作就方便多了，
若要删除左图的(v0,v2)这条边，只需要将右图的（6）（9）的链接指向改为^即可。

代码实现前的思考：

MMP,怎么就想不出来用什么方法去存储这些边呢？顶点和边不对应呀....吐血....，去网上找找其他关于邻接多重表的信息吧

数据结构之图(2-2)【邻接多重表】适用于无向图

无向图的邻接多重表存储结构

这两篇文章来了思路，将表的结构修改一下，我们只需要保证邻接多重表的根本，就是创建边表，而不是创建顶点表，因为顶点表是边表的两倍，在删除时会导致重复操作，而我们的边表只需要创建对应边数的结点，删除某条边，就删除对应结点即可。不需要重复操作。

 

 

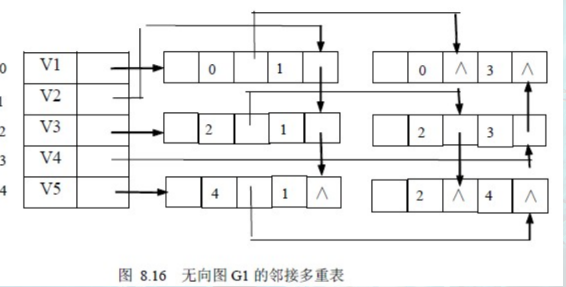
上面这种表示方法，但是好像没说清楚为啥这么排列。

于是决定测试将对应顶点的邻接边全部放入顶点后面

步骤一：先排序第一个顶点的所有邻接边

步骤二：我们再排序第二个顶点的所有邻接边

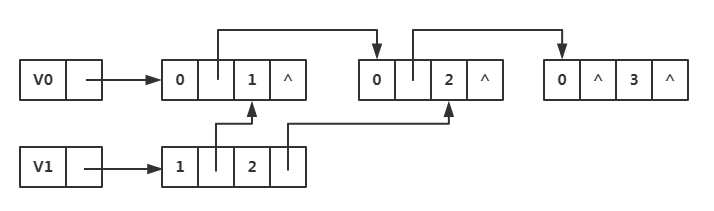
步骤三：我们接着排序第三个顶点的所有邻接边

步骤四：开始排序最后一个顶点所有邻接边

 

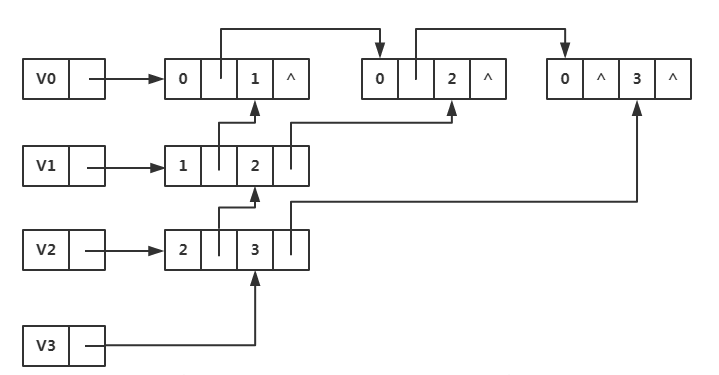
 通过上面排序，我们可以获取所有邻接点和邻接边

 按照上面来实现代码

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define MAXVEX 100    //最大顶点数

typedef char VertexType;    //顶点类型，字符型A,B,C,D...
typedef int EdgeType;    //边上权值类型10,15,...

typedef struct ENode    //十字链表结点
{
    int ivex, jvex;    //表示两个顶点下标，构成了一条边。
    int weight;            //用于存放权值，对于非网图可以不需要
    struct ENode* ilink;    //邻接多重表，指向下一个邻接点，
    struct ENode* jlink;    //邻接多重表，指向下一个邻接点，
}ENode;

typedef struct VertexNode   //顶点表结点
{
    VertexType data;    //顶点域，存储顶点信息
    ENode* firstedge;    //边表头指针
}VertexNode, AMLList[MAXVEX];

typedef struct
{
    AMLList adjList;    //邻接多重表数组
    int numVertexes, numEdges;    //图中所存储的顶点数和边数
}AMLGraphList;

//根据ivex找到第几行，我们去前面几行查找,jvex获取下标
ENode* GetNode(AMLGraphList* G,int ivex,int jvex)
{
    int i;
    ENode *e;
    for (i = ivex-1; i >=0;i--)
    {
        e = G->adjList[i].firstedge;
        while (e)
        {
            if (e->jvex==jvex)
            {
                return e;
            }
            e = e->ilink;
        }
    }

    return NULL;
}

void CreateAMLGraph(AMLGraphList* G)
{
    int i, j, k, w,flag;
    ENode *e;
    ENode *tempNode;
    printf("please input number of vertex and edge:\n");
    scanf("%d,%d", &G->numVertexes, &G->numEdges);    //输入顶点数和边数
    getchar();    //可以获取回车符
    for (i = 0; i < G->numVertexes; i++)    //输入顶点信息
    {
        scanf("%c", &G->adjList[i].data);    //输入顶点信息
        G->adjList[i].firstedge = NULL;    //将边表置为空
    }
    getchar();    //可以获取回车符

    //先循环获取边信息。创建所有边信息,放在对应的顶点后面，
    for (k = 0; k < G->numEdges; k++)
    {
        printf("Out-->input edge(vi,vj) vertexs series and the weight:\n");
        scanf("%d,%d,%d", &i, &j, &w);
        getchar();
        //创建邻接多重表结点
        e = (ENode *)malloc(sizeof(ENode));
        //使用头插法将数据插入（主要是头插法方便），我们插入不需要考虑顺序，因为链表结点都是与数组顶点相连接的
        e->ivex = i;
        e->jvex = j;
        e->weight = w;
        e->ilink = G->adjList[i].firstedge;
        e->jlink = NULL;
        G->adjList[i].firstedge = e;
    }

    //开始连接多张表之间的关系，并且判断ilink和jlink，从第二个顶点开始
    for (i = 1; i < G->numVertexes;i++)
    {
        e = G->adjList[i].firstedge;
        if (e)
        {
            flag = 0;    //用来标识是不是最后一个结点
            while (e&&!flag)    //需要将最后一个单独处理
            {
                if (e->ilink == NULL)
                {
                    tempNode = GetNode(G, i, e->ivex);
                    e->ilink = tempNode;
                    flag = 1;
                }
                tempNode = GetNode(G, i, e->jvex);
                e->jlink = tempNode;

                e = e->ilink;
            }
            //e = GetNode(G, i, e->jvex);    //处理最后一个
        }
        else
            G->adjList[i].firstedge = GetNode(G, i, i);
    }
}

int main()
{
    AMLGraphList gl;
    CreateAMLGraph(&gl);
    gl;
    system("pause");
    return 0;
}

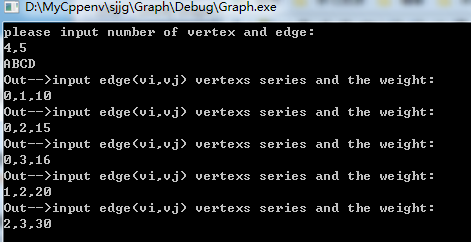
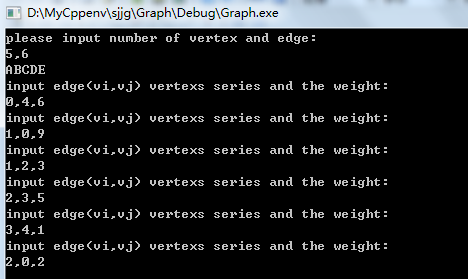
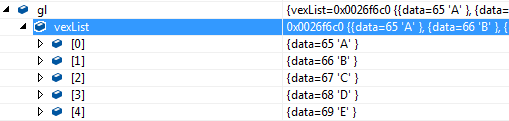
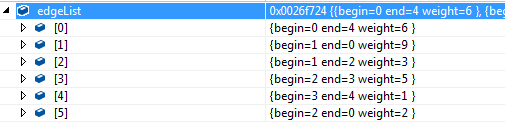
七：图的存储结构（5）---边集数组

边集数组是由两个一维数组构成。一个是存储顶点的信息；另一个是存储边的信息。
这个边数组每个数据元素由一条边的起点下标（begin）、终点下标（end）和权（weight）组成。

结构

表现

如上图所示，边集数组关注的是边的集合，在边集数组中要查找一个顶点的度需要扫描整个边数组，效率并不高。
因此它更适合对边依次进行处理的操作，而不适合对顶点相关的操作。

 代码实现

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define MAXVEX 100    //最大顶点数

typedef char VertexType;    //顶点类型，字符型A,B,C,D...
typedef int EdgeType;    //边上权值类型10,15,...

typedef struct VertexNode   //顶点表结点
{
    VertexType data;    //顶点域，存储顶点信息
}VertexNode, VertexList[MAXVEX];

typedef struct EdgeNode   //边集表结点
{
    int begin, end, weight;
}EdgeNode, EdgeList[MAXVEX];

typedef struct
{
    VertexList vexList;    //顶点表
    EdgeList edgeList;    //边集表
    int numVertexes, numEdges;    //图中所存储的顶点数和边数
}EdgeGraphList;


void CreateEdgeGraph(EdgeGraphList* G)
{
    int i, j ,k,w;
    printf("please input number of vertex and edge:\n");
    scanf("%d,%d",&G->numVertexes,&G->numEdges);    //输入顶点数和边数
    getchar();    //可以获取回车符

    //获取顶点数组信息
    for (i = 0; i < G->numVertexes;i++)    //输入顶点信息
    {
        scanf("%c", &G->vexList[i].data);    //输入顶点信息
    }

    //获取边数组
    for (k = 0; k < G->numEdges;k++)
    {
        printf("input edge(vi,vj) vertexs series and the weight:\n");
        scanf("%d,%d,%d", &i, &j,&w);
        getchar();
        //由于是无向图，对称矩阵，当我们设置边以后，需要在两个地方设置结点
        G->edgeList[k].begin = i;
        G->edgeList[k].end = j;
        G->edgeList[k].weight = w;
    }
}

int main()
{
    EdgeGraphList gl;
    CreateEdgeGraph(&gl);
    gl;
    system("pause");
    return 0;
}