数据结构(四)树---树的转换
(一)树转二叉树
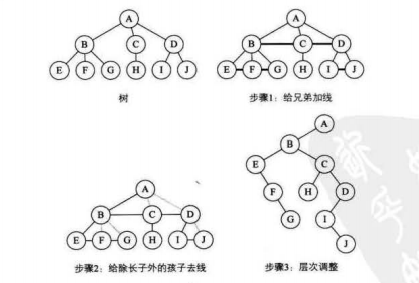
步骤
1.加线:在所有兄弟结点之间加一条连线 2.去线:对树中每个结点,只保留他与第一个长子结点的连线,删除他与其他孩子结点之间的连线 3.层次调整。以树的根节点为轴心,将整棵树顺时针旋转一定角度,使结构层次分明。 注意:第一个孩子是二叉树结点的左孩子,兄弟转换过来的孩子是结点的右孩子
转换后,根节点只有左子树,最左侧链表不改变
(二)森林转二叉树

步骤
1.将每个树转换为二叉树 2.第一棵二叉树不动,从第二棵二叉树开始,依次吧后一棵二叉树的根节点作为前一棵二叉树的根节点的右子树,用线连接起来。当所有的二叉树连接起来,就得到了由森林转换而来的二叉树
(三)二叉树转换为树

步骤
1.若某结点的左孩子存在,则将该左孩子的右孩子结点,以及该左孩子的右孩子的右孩子结点,以及...,就是左孩子的n个右孩子结点都作为此结点的孩子。将该结点与这些右孩子结点用线连接 2.去线:删除原二叉树中所有结点与其右孩子结点的连线
(四)二叉树转森林
我们从一:知道树转二叉树只有左子树,森林转二叉树会同时存在左子树和右子树
所以判断一棵树能够转换为一棵树还是一个森林,就看这个二叉树的根节点有没有右孩子
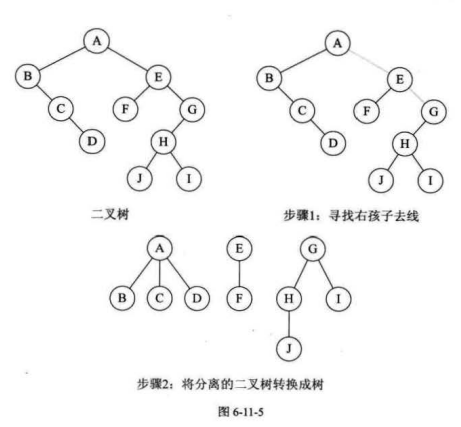
步骤
1.从根节点开始,若是右孩子存在,将右链拆开,所有的右孩子连线都删除。得到分离的二叉树。
2.再将每棵分离后的二叉树转换为树即可
(五)树的遍历
法一:先根遍历
先根遍历树,即先访问树的根节点,然后依次先根遍历根的每棵子树(类似于先序遍历)
法二:后根遍历
后根遍历,即先依次后根遍历每棵子树,然后再访问根节点。(类似于后序遍历)
(六)森林的遍历
法一:前序遍历
先访问森林的第一棵树的根节点,然后依次先根遍历....,再依次用同样方法遍历下一棵树....
法二:后序遍历
先访问森林的第一棵树的根节点,然后依次后根遍历....,再依次用同样方法遍历下一棵树....
(七)总结
树,森林的前根(序)遍历和二叉树的前序遍历结果相同,树,森林的后根(序)遍历和二叉树的中序遍历结果相同
可以根据(一)和(二)轻松推出结论,然后利用这种规律,解决这些复杂的树,森林遍历问题
(八)代码实现:创建树,实现树转换二叉树,利用二叉树打印出树的结果
#define _CRT_SECURE_NO_WARNINGS #include <stdio.h> #include <stdlib.h> typedef char TElemType;//树的孩子兄弟表示法结构定义 typedef struct TNode //结点结构 { TElemType data; //结点数据 struct TNode *lchild, *rsibling; //左孩子,右兄弟指针 }TNode, *Tree; //二叉树的二叉链表结点结构定义 typedef struct BiTNode //结点结构 { TElemType data; //结点数据 struct BiTNode *lchild, *rchild; //左右孩子指针 }BiTNode, *BiTree; //使用孩子兄弟法创建一棵树 //创建一棵树ABDG#H#I###CEJ##F#### void createTree(Tree *T) { TElemType ch; scanf("%c", &ch); if (ch == '#') *T = NULL; else { *T = (Tree)malloc(sizeof(TNode)); (*T)->data = ch; createTree(&(*T)->lchild); //构造左孩子 createTree(&(*T)->rsibling);//构造右兄弟 } } void Tree2BiTree(Tree T,BiTree *BT) { if (T) { *BT = (BiTree)malloc(sizeof(BiTNode)); (*BT)->data = T->data; Tree2BiTree(T->lchild, &(*BT)->lchild); //利用对应的结点来构造二叉树 Tree2BiTree(T->rsibling, &(*BT)->rchild); } else *BT = NULL; } //传入的是转换为二叉树的树 void PreOrderTraverseForTree(BiTree BT) { if (BT) { printf("%c", BT->data); PreOrderTraverseForTree(BT->lchild); PreOrderTraverseForTree(BT->rchild); } } int main() { Tree T; BiTree BT; createTree(&T); Tree2BiTree(T,&BT); PreOrderTraverseForTree(BT); system("pause"); return 0; }




