(一)前提
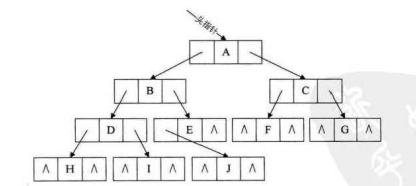
对于我们的二叉树,依旧有n+1个指针域未被利用起来,也就是存在着n+1个空指针域。我们要做的就是:要么节省要么利用。
对于上面的案例:我们选用中序遍历获取结果
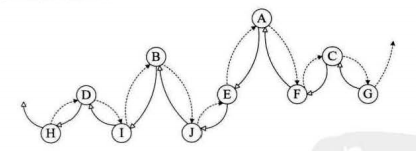
利用中序遍历:刚好他们处于字符中间,所以我们可以很好的利用这些空指针域,使他来存放前驱和后继的指针。方便我们进行遍历,形成类似于双向链表的形式
当然,上面我们只是拿出来一个特殊的案例,还有很多普通案例,例如一个结点中只有一个空指针域等等...,我们应该思考一个结点的指针域中到底是存放指针还是线索
(二)定义
我们把这种指向前驱和后继的指针称为线索,加上线索的二叉链表称为线索链表,相应的二叉树就称为线索二叉树Threaded Binary Tree
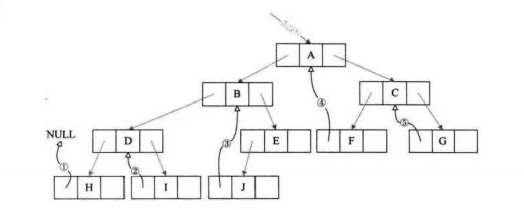
其实线索二叉树,就是把一棵二叉树转变为一个双向链表,这样我们的插入删除结点,查找某个结点都带来了方便。所以我们对二叉树一某种次序遍历使其变为线索二叉树的过程称作是线索化
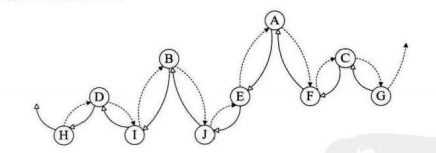

注意:新加入的两个标志域ltag和rtag只是存放0或1数字的布尔型变量,其内存占用小于指针变量
(三)二叉树线索化实现
1.创建二叉树
#include <stdio.h>
#include <stdlib.h>
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
typedef char TElemType;
typedef int Status;
typedef enum {Link,Thread} PointerTag;
//二叉树的二叉链表结点结构定义
typedef struct BiTNode //结点结构
{
TElemType data; //结点数据
struct BiTNode *lchild, *rchild; //左右孩子指针
PointerTag ltag;
PointerTag rtag;
}BiThrNode, *BThriTree;
//按照前序输入二叉树中结点的值(一个字符)
//#表示空树,构造二叉树表表示二叉树T
void CreateBiThrTree(BThriTree *T)
{
TElemType ch;
scanf("%c", &ch);
if (ch == '#')
*T = NULL;
else
{
*T = (BThriTree)malloc(sizeof(BiThrNode));
if (!*T)
exit(ERROR);
(*T)->data = ch; //生成根节点数据
(*T)->ltag = Link;
(*T)->rtag = Link;
CreateBiTree(&(*T)->lchild); //构造左子树
CreateBiTree(&(*T)->rchild); //构造右子树
}
}
2.线索化二叉树
注意:对于二叉树原来的边都是Link,我们后加的都是Thread,不能破坏二叉树
BThriTree pre; //始终指向前驱结点,使用它来保存前驱,会在线索化函数中实时修改
//进行线索化
//中序遍历线索化
void InThreading(BThriTree T)
{
if (T)
{
InThreading(T->lchild); //递归左子树线索化
//进行线索化操作
if (!T->lchild) //若是没有左孩子,进行线索化
{
T->ltag = Thread; //前驱线索
T->lchild = pre; //左孩子指针指向前驱
}
//我们这里是想要对该T结点进行线索化
/*
if (!T->rchild)
{
T->rtag = Thread;
T->rchild = 下一个后继结点
}
*/
//但是我们无法知道下一个后继结点位置
//我们可以反向思考,我们根据当前节点去推断前驱结点是不是可以向右线索化,来配置
if (!pre->rchild) //前驱没有右孩子
{
pre->rtag = Thread; //后继线索
pre->rchild = T; //前驱有孩子指向后继(当前节点p)
}
pre = T; //将前驱推移,始终保持pre执行p的前驱
InThreading(T->rchild); //递归右子树线索化
}
}
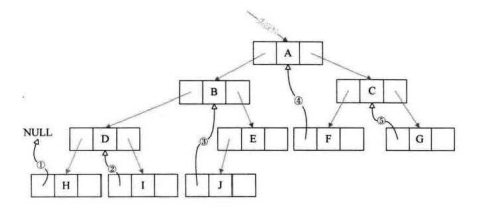
上面红色部分的pre指针,会在函数调用的时候就会跟着去调用,但是此时的pre指针为0,空指针异常,所以一定会报错,那么我们应该如何处理
3.思考pre指针
注意:此时我们的pre为空,但是我们在开始线索化时候就已经开始使用pre指针,这会导致出错
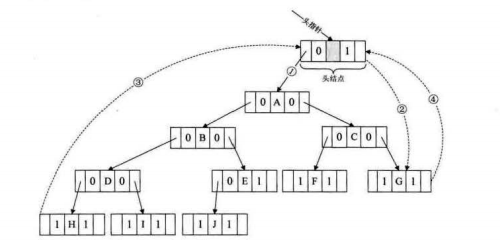
使头结点的左lchild(Link)指向二叉树的根节点,右rchild域(Thread)的指针指向中序遍历访问的最后一个结点。
反之,使二叉树的中序序列的第一个结点的lchild域指针和最后一个结点的rchild与指针均指向头结点。
这样我们就可以既可以从第一个结点起,按后继进行遍历,也可以从最后一个结点起,按前驱进行遍历
//在线索化前设置头结点
InOrderThreading(BThriTree* p,BThriTree T)
{
*p = (BThriTree)malloc(sizeof(BiThrNode));
(*p)->ltag = Link;
(*p)->rtag = Thread;
//按树的结构设置头结点
//使他指向自己,下面判断是不是空树,再进行指向
(*p)->rchild = *p;
if (!T) //T是空树的情况
{
(*p)->lchild = *p;
}
else
{
//使得头结点指向根节点
(*p)->lchild = T;
pre = *p;
//对所有的含有空指针域的结点进行线索化,从根节点开始,不包含头结点
InThreading(T);
//线索化后将中序遍历最后的结点指向头结点
pre->rchild = *p;
pre->rtag = Thread;
(*p)->rchild = pre;
}
}
既然不能是pre为空,那我们就去利用他,使他变为头结点。方便我们进行遍历。注意:头结点是指向根节点的,不能破坏原来二叉树的结构
(四)根据线索化的二叉树进行非递归遍历(遍历双向链表)
//我们是使用中序方法来线索化二叉树,所以使用中序来遍历是最方便的
void InOrderTraverse(BThriTree T) //我们传入的是线索化带有头结点的树
{
BThriTree p;
p = T->lchild; //这是根节点
while (p != T) //可以直接按照双向链表来处理二叉树了
{
while (p->ltag == Link) //当我们找到了Thread时就是找到了最左边的结点,是双向链表的开始结点
{
p = p->lchild;
}
printf("%c", p->data);
while (p->rtag==Thread&&p->rchild!=T) //while我们可以通过特殊二叉树,左斜二叉树看出是有必要的
{
p = p->rchild;
printf("%c", p->data);
}
p = p->rchild;
}
}
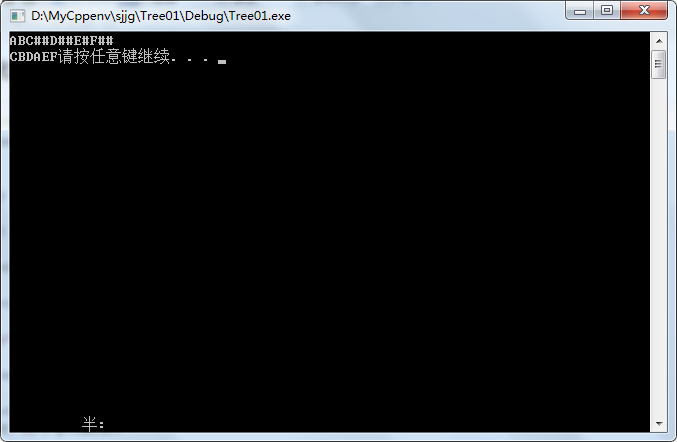
int main()
{
BThriTree T,P;
CreateBiThrTree(&T);
InOrderThreading(&P, T);
InOrderTraverse(P);
system("pause");
return 0;
}
(五)全部代码
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
typedef char TElemType;
typedef int Status;
typedef enum {Link,Thread} PointerTag;
//二叉树的二叉链表结点结构定义
typedef struct BiTNode //结点结构
{
TElemType data; //结点数据
struct BiTNode *lchild, *rchild; //左右孩子指针
PointerTag ltag;
PointerTag rtag;
}BiThrNode, *BThriTree;
//按照前序输入二叉树中结点的值(一个字符)
//#表示空树,构造二叉树表表示二叉树T
void CreateBiThrTree(BThriTree *T)
{
TElemType ch;
scanf("%c", &ch);
if (ch == '#')
*T = NULL;
else
{
*T = (BThriTree)malloc(sizeof(BiThrNode));
if (!*T)
exit(ERROR);
(*T)->data = ch; //生成根节点数据
(*T)->ltag = Link;
(*T)->rtag = Link;
CreateBiThrTree(&(*T)->lchild); //构造左子树
CreateBiThrTree(&(*T)->rchild); //构造右子树
}
}
BThriTree pre; //始终指向前驱结点
//进行线索化
//中序遍历线索化
void InThreading(BThriTree T)
{
if (T)
{
InThreading(T->lchild); //递归左子树线索化
//进行线索化操作
if (!T->lchild) //若是没有左孩子,进行线索化
{
T->ltag = Thread; //前驱线索
T->lchild = pre; //左孩子指针指向前驱
}
//我们这里是想要对该T结点进行线索化
/*
if (!T->rchild)
{
T->rtag = Thread;
T->rchild = 下一个后继结点
}
*/
//但是我们无法知道下一个后继结点位置
//我们可以反向思考,我们根据当前节点去推断前驱结点是不是可以向右线索化,来配置
if (!pre->rchild) //前驱没有右孩子
{
pre->rtag = Thread; //后继线索
pre->rchild = T; //前驱有孩子指向后继(当前节点p)
}
pre = T; //将前驱推移,始终保持pre执行p的前驱
InThreading(T->rchild); //递归右子树线索化
}
}
//在线索化前设置头结点
InOrderThreading(BThriTree* p,BThriTree T)
{
*p = (BThriTree)malloc(sizeof(BiThrNode));
(*p)->ltag = Link;
(*p)->rtag = Thread;
//按树的结构设置头结点
//使他指向自己,下面判断是不是空树,再进行指向
(*p)->rchild = *p;
if (!T) //T是空树的情况
{
(*p)->lchild = *p;
}
else
{
//使得头结点指向根节点
(*p)->lchild = T;
pre = *p;
//对所有的含有空指针域的结点进行线索化,从根节点开始,不包含头结点
InThreading(T);
//线索化后将中序遍历最后的结点指向头结点
pre->rchild = *p;
pre->rtag = Thread;
(*p)->rchild = pre;
}
}
//我们是使用中序方法来线索化二叉树,所以使用中序来遍历是最方便的
void InOrderTraverse(BThriTree T) //我们传入的是线索化带有头结点的树
{
BThriTree p;
p = T->lchild; //这是根节点
while (p != T) //可以直接按照双向链表来处理二叉树了
{
while (p->ltag == Link) //当我们找到了Thread时就是找到了最左边的结点,是双向链表的开始结点
{
p = p->lchild;
}
printf("%c", p->data);
p = p->rchild;
printf("%c", p->data);
p = p->rchild;
}
}
int main()
{
BThriTree T,P;
CreateBiThrTree(&T);
InOrderThreading(&P, T);
InOrderTraverse(P);
system("pause");
return 0;
}










