数据结构（四）树---二叉树实现

（一）顺序结构创建二叉树

#include <stdio.h>
#include <stdlib.h>
#include <math.h>

#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0

#define MAXSIZE 100    //存储空间初始分配量
#define MAX_TREE_SIZE 100    //二叉树的最大结点数

typedef char TElemType;
typedef int Status;

typedef TElemType SqBiTree[MAX_TREE_SIZE];    //定义顺序二叉树的结构

typedef struct
{
    int level, order;    //结点的层，本层的序号
}Position;

TElemType Nil = '^';    //设置结点以^为空

Status InitBiTree(SqBiTree T);    //构造空二叉树T，因为T是固定数组，不会改变，故不需要&
Status CreateBiTree(SqBiTree T);//按照层序次序输入二叉树中结点的值，构造顺序存储的二叉树
Status BiTreeEmpty(SqBiTree T);//判断二叉树是否为空
int BiTreeDepth(SqBiTree T);//获取二叉树的深度
Status Root(SqBiTree T, TElemType* e);//返回根节点数据
TElemType Value(SqBiTree T, Position e);//获取具体位置的结点值
Status Assign(SqBiTree T, Position e, TElemType value);//对某个叶子结点赋值
TElemType Parent(SqBiTree T, TElemType e);//根据元素，获取其双亲结点的值
TElemType LeftChild(SqBiTree T, TElemType e);//返回结点的左孩子
TElemType RightChild(SqBiTree T, TElemType e);//返回结点的右孩子
TElemType LeftSibling(SqBiTree T, TElemType e);//返回结点的左兄弟
TElemType RightSibling(SqBiTree T, TElemType e);//返回结点的右兄弟
void PreOrderTraverse(SqBiTree T, int e);//开始进行前序遍历
void InOrderTraverse(SqBiTree T, int e);//开始进行中序遍历
void PostOrderTraverse(SqBiTree T, int e);//开始进行后序遍历
void LevelOrderTraverse(SqBiTree T);//开始进行层序遍历

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <math.h>

#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0

#define MAXSIZE 100    //存储空间初始分配量
#define MAX_TREE_SIZE 100    //二叉树的最大结点数

typedef char TElemType;
typedef int Status;

typedef TElemType SqBiTree[MAX_TREE_SIZE];    //定义顺序二叉树的结构

typedef struct
{
    int level, order;    //结点的层，本层的序号
}Position;

TElemType Nil = '^';    //设置结点以^为空


//构造空二叉树T，因为T是固定数组，不会改变，故不需要&
Status InitBiTree(SqBiTree T)
{
    int i;
    for (i = 0; i < MAX_TREE_SIZE; i++)
        T[i] = Nil;
    return OK;
}

//按照层序次序输入二叉树中结点的值，构造顺序存储的二叉树T
Status CreateBiTree(SqBiTree T)
{
    int i = 0;
    char ch;
    printf("please enter value for node(^ is Nil,# exit) number must <= %d:\n",MAX_TREE_SIZE);
    scanf("%c", &ch);
    while (ch!='#')
    {
        T[i++] = ch;
        if (i != 0 && T[i] != Nil &&T[(i + 1) / 2 - 1] == Nil)    //不为根节点，自己又不为空，父节点又不存在，一定是错的
        {
            printf("exist a node not parents node:%c",T[i]);
            exit(ERROR);
        }
        scanf("%c", &ch);
    }
    //将后面的结点全部置为空：是为了防止使用时创建两次二叉树，出现数据冗余
    while (i<MAX_TREE_SIZE)
    {
        T[i++] = Nil;    //将空值赋给T后面的结点
    }
    return OK;
}

#define ClearBiTree InitBiTree    //在顺序存储结构中，两者是一致的

//判断二叉树是否为空
Status BiTreeEmpty(SqBiTree T)
{
    if (T[0] == Nil)
        return TRUE;
    return FALSE;
}

//获取二叉树的深度
int BiTreeDepth(SqBiTree T)
{
    int i, j=-1;
    for (i = MAX_TREE_SIZE-1; i >= 0; i--)    //获取最后一个结点
        if (T[i] != Nil)
            break;
    //根据pow判断深度
    i++;    //获取从1开始的二叉树，而不是以0开始，方便下面计算
    do 
    {
        j++;
    } while (i>=pow(2,j));
    return j;
}

//返回根节点数据
Status Root(SqBiTree T, TElemType* e)
{
    if (BiTreeEmpty(T))
        return ERROR;
    *e = T[0];
    return OK;
}

//获取具体位置的结点值
TElemType Value(SqBiTree T, Position e)
{
    return T[(int)pow(2,e.level-1)-2+e.order];
}

//对某个叶子结点赋值
Status Assign(SqBiTree T, Position e, TElemType value)
{
    //先将e转换Wie一维数组的下标
    int index = (int)pow(2, e.level - 1) - 2 + e.order;
    //判断其双亲是否存在
    if (index != 0 && T[(index + 1) / 2 - 1] == Nil)
        return ERROR;
    //若是我们赋值为空，但是其子节点存在，也返回空
    if (value == Nil && (T[index * 2 + 1] != Nil || T[index * 2 + 2] != Nil))
        return ERROR;
    T[index] = value;
    return OK;
}

//根据元素，获取其双亲结点的值
TElemType Parent(SqBiTree T, TElemType e)
{
    int i;
    //若是空树
    if (T[0] == Nil)
        return Nil;
    for (i = 1; i < MAX_TREE_SIZE; i++)    //注意这里从1开始，若是出现在头结点，会直接在下面返回Nil
        if (T[i] == e)    //找到该结点
            return T[(i + 1) / 2 - 1];
    return Nil;
}

//返回结点的左孩子
TElemType LeftChild(SqBiTree T, TElemType e)
{
    int i;
    //若是空树
    if (T[0] == Nil)
        return Nil;
    for (i = 1; i < MAX_TREE_SIZE; i++)    //注意这里从1开始，若是出现在头结点，会直接在下面返回Nil
        if (T[i] == e)    //找到该结点
            return T[2*i+1];
    return Nil;
}

//返回结点的右孩子
TElemType RightChild(SqBiTree T, TElemType e)
{
    int i;
    //若是空树
    if (T[0] == Nil)
        return Nil;
    for (i = 1; i < MAX_TREE_SIZE; i++)    //注意这里从1开始，若是出现在头结点，会直接在下面返回Nil
        if (T[i] == e)    //找到该结点
            return T[2 * i + 2];
    return Nil;
}

//返回结点的左兄弟
TElemType LeftSibling(SqBiTree T, TElemType e)
{
    int i;
    //若是空树
    if (T[0] == Nil)
        return Nil;
    for (i = 1; i < MAX_TREE_SIZE; i++)    //注意这里从1开始，若是出现在头结点，会直接在下面返回Nil
        if (T[i] == e&&i%2==0)    //找到右节点
            return T[i-1];
    return Nil;
}

//返回结点的右兄弟
TElemType RightSibling(SqBiTree T, TElemType e)
{
    int i;
    //若是空树
    if (T[0] == Nil)
        return Nil;
    for (i = 1; i < MAX_TREE_SIZE; i++)    //注意这里从1开始，若是出现在头结点，会直接在下面返回Nil
        if (T[i] == e&&i % 2 == 1)    //找到左节点
            return T[i + 1];
    return Nil;
}

//开始进行前序遍历
void PreOrderTraverse(SqBiTree T,int e)
{
    if (T&&e<MAX_TREE_SIZE)
    {
        if (T[e] != Nil)
            printf("%c", T[e]);
        PreOrderTraverse(T, 2 * e + 1);
        PreOrderTraverse(T, 2 * e + 2);
    }
}

//开始进行中序遍历
void InOrderTraverse(SqBiTree T, int e)
{
    if (T&&e<MAX_TREE_SIZE)
    {
        InOrderTraverse(T, 2 * e + 1);
        if (T[e] != Nil)
            printf("%c", T[e]);
        InOrderTraverse(T, 2 * e + 2);
    }
}

//开始进行后序遍历
void PostOrderTraverse(SqBiTree T, int e)
{
    if (T&&e<MAX_TREE_SIZE)
    {
        PostOrderTraverse(T, 2 * e + 1);
        PostOrderTraverse(T, 2 * e + 2);
        if (T[e]!=Nil)
            printf("%c", T[e]);
    }
}

//开始进行层序遍历
void LevelOrderTraverse(SqBiTree T)
{
    int i = MAX_TREE_SIZE - 1;
    int j;
    while (T[i] == Nil)
        i--;
    for (j = 0; j <= i; j++)
        if (T[j] != Nil)
            printf("%c", T[j]);    //值获取非空数据
}

int main()
{
    TElemType e;
    Status i;
    Position p; 
    SqBiTree T;
    printf("1.InitBiTree\n");
    InitBiTree(T);
    printf("2.CreateBiTree\n");
    CreateBiTree(T);
    printf("3.LevelOrderTraverse\n");
    LevelOrderTraverse(T);
    printf("\n");
    printf("4.PreOrderTraverse\n");
    PreOrderTraverse(T,0);
    printf("\n");
    printf("5.InOrderTraverse\n");
    InOrderTraverse(T,0);
    printf("\n");
    printf("6.PostOrderTraverse\n");
    PostOrderTraverse(T, 0);
    printf("\n");
    printf("7.PostOrderTraverse\n");
    if (Root(T, &e))
        printf("8.Root:%d\n", e);
    printf("9.PostOrderTraverse\n");
    printf("10.LeftChild for D --> %c\n", LeftChild(T, 'D'));
    printf("11.RightChild for D --> %c\n", RightChild(T, 'D'));
    printf("12.LeftSibling for H --> %c\n", LeftSibling(T, 'H'));
    printf("13.RightSibling for G --> %c\n", RightSibling(T, 'G'));
    printf("14.BiTreeDepth:%d\n", BiTreeDepth(T));
    p.level = 4;
    p.order = 2;
    printf("15.Value row4 col2:Z\n");
    Assign(T, p, 'Z');
    LevelOrderTraverse(T);

    system("pause");
    return 0;
}

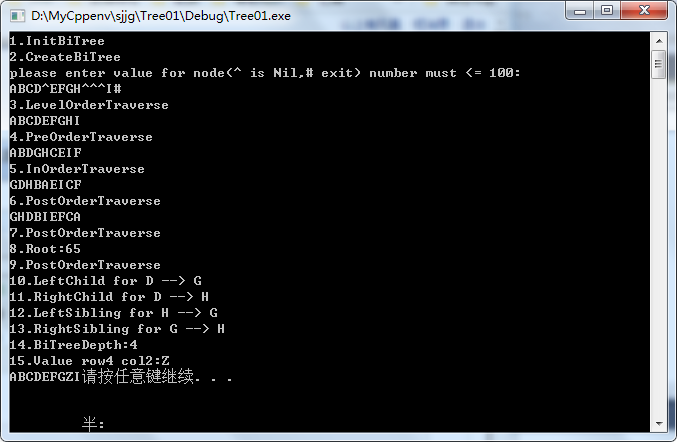
（二）链式结构创建二叉树

//按照前序输入二叉树中结点的值（一个字符）
//#表示空树，构造二叉树表表示二叉树T
void CreateBiTree(BiTree *T)
{
    TElemType ch;
    scanf("%c", &ch);
    if (ch == '#')
        *T = NULL;
    else
    {
        *T = (BiTree)malloc(sizeof(BiTNode));
        if (!*T)
            exit(ERROR);
        (*T)->data = ch;    //生成根节点数据
        CreateBiTree(&(*T)->lchild);    //构造左子树
        CreateBiTree(&(*T)->rchild);    //构造右子树
    }
}

（三）使用递归实现对二叉树的遍历

#include <stdio.h>
#include <stdlib.h>

#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0

#ifndef BINTREE_H
#define BINTREE_H
typedef char TElemType;
typedef int Status;

//二叉树的二叉链表结点结构定义
typedef struct BiTNode    //结点结构
{
    TElemType data;    //结点数据
    struct BiTNode *lchild, *rchild;    //左右孩子指针
}BiTNode, *BiTree;
#endif

#define _CRT_SECURE_NO_WARNINGS
#include "BinT.h"
void PreOrderTraverse(BiTree T, int level)
{
    if (T)
    {
        printf("%c in level %d\n", T->data,level + 1);
        PreOrderTraverse(T->lchild, level + 1);
        PreOrderTraverse(T->rchild, level + 1);
    }
}

void InOrderTraverse(BiTree T, int level)
{
    if (T)
    {
        InOrderTraverse(T->lchild, level + 1);
        printf("%c in level %d\n", T->data, level + 1);
        InOrderTraverse(T->rchild, level + 1);
    }
}


void PostOrderTraverse(BiTree T, int level)
{
    if (T)
    {
        PostOrderTraverse(T->lchild, level + 1);
        PostOrderTraverse(T->rchild, level + 1);
        printf("%c in level %d\n", T->data, level + 1);
    }
}


int main()
{
    BiTree T;
    printf("1.CreateBiTree\n");
    CreateBiTree(&T);
    printf("2.PreOrderTraverse\n");
    PreOrderTraverse(T, 0);
    printf("3.InOrderTraverse\n");
    InOrderTraverse(T, 0);
    printf("4.PostOrderTraverse\n");
    PostOrderTraverse(T, 0);
    
    system("pause");
    return 0;
}

（四）.使用栈实现非递归，遍历二叉树

#include <stdio.h>
#include <stdlib.h>
#include "BinT.h"

#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0

#define MAXSIZE 100

typedef BiTree ElemType;

typedef struct
{
    ElemType data[MAXSIZE];
    int top;
}sqStack;

Status InitStack(sqStack *s);    //初始化操作，建立一个空栈
Status ClearStack(sqStack *s);    //将栈清空
Status StackEmpty(sqStack s);    //若栈存在，返回true，否则返回false

Status Push(sqStack *s, ElemType e);    // 若是栈存在，则插入新的元素e到栈S中并成为栈顶元素
Status Pop(sqStack *s, ElemType *e);    //若是栈存在且非空，删除栈顶元素，并用e返回其值

#define _CRT_SECURE_NO_WARNINGS
#include "stack.h"

//初始化操作，建立一个空栈
Status InitStack(sqStack *s)
{
    if (!s)
        return ERROR;
    memset(s->data, 0, MAXSIZE*sizeof(ElemType));
    s->top = -1;
    return OK;
}

//将栈清空
Status ClearStack(sqStack *s)
{
    if (!s)
        return ERROR;
    s->top = -1;
    return OK;
}

//若栈存在，返回true，否则返回false
Status StackEmpty(sqStack s)
{
    if (s.top == -1)
        return OK;
    return ERROR;
}

// 若是栈存在，则插入新的元素e到栈S中并成为栈顶元素
Status Push(sqStack *s, ElemType e)
{
    if (s->top == MAXSIZE||!s)
        return ERROR;
    s->top++;
    s->data[s->top] = e;
    return OK;
}

//若是栈存在且非空，删除栈顶元素，并用e返回其值
Status Pop(sqStack *s, ElemType *e)
{
    if (!s || StackEmpty(*s) || !e)
        return ERROR;
    *e = s->data[s->top--];
    return OK;
}

void PreOrderTraverseByStack(BiTree BT)
{
    BiTree T = BT;
    sqStack s;
    InitStack(&s);
    while (T || !StackEmpty(s))
    {
        while (T)
        {
            printf("%c", T->data);
            Push(&s, T);
            T = T->lchild;
        }
        if (!StackEmpty(s))
        {
            Pop(&s, &T);
            T = T->rchild;
        }
    }
    printf("\n");
}

void InOrderTraverseByStack(BiTree BT)
{
    BiTree T = BT;
    sqStack s;
    InitStack(&s);
    while (T || !StackEmpty(s))
    {
        while (T)
        {
            Push(&s, T);
            T = T->lchild;
        }
        if (!StackEmpty(s))
        {
            Pop(&s, &T);
            printf("%c", T->data);
            T = T->rchild;
        }
    }
    printf("\n");
}
void PostOrderTraverseByStack(BiTree BT)
{
    BiTree T = BT;
    sqStack s;
    InitStack(&s);
    while (T||!StackEmpty(s))
    {
        while (T)
        {
            Push(&s, T);
            T = T->lchild;
        }
        if (!StackEmpty(s))
        {
            Pop(&s, &T);
            if (!T->rchild||T->first==2)
            {
                printf("%c", T->data);
                T = NULL;
            }
            else
            {
                T->first = 2;
                Push(&s,T);
                T = T->rchild;
            }
        }
    }
    printf("\n");
}

//二叉树的二叉链表结点结构定义
typedef struct BiTNode    //结点结构
{
    TElemType data;    //结点数据
    int first;    //对于非递归后序而言
    struct BiTNode *lchild, *rchild;    //左右孩子指针
}BiTNode, *BiTree;

int main()
{
    BiTree T;
    printf("1.CreateBiTree\n");
    CreateBiTree(&T);
    printf("2.PreOrderTraverse\n");
    PreOrderTraverse(T, 0);
    printf("3.InOrderTraverse\n");
    InOrderTraverse(T, 0);
    printf("4.PostOrderTraverse\n");
    PostOrderTraverse(T, 0);
    printf("5.PreOrderTraverseByStack\n");
    PreOrderTraverseByStack(T);
    printf("6.InOrderTraverseByStack\n");
    InOrderTraverseByStack(T);
    printf("7.PostOrderTraverseByStack\n");
    PostOrderTraverseByStack(T);
    
    system("pause");
    return 0;
}

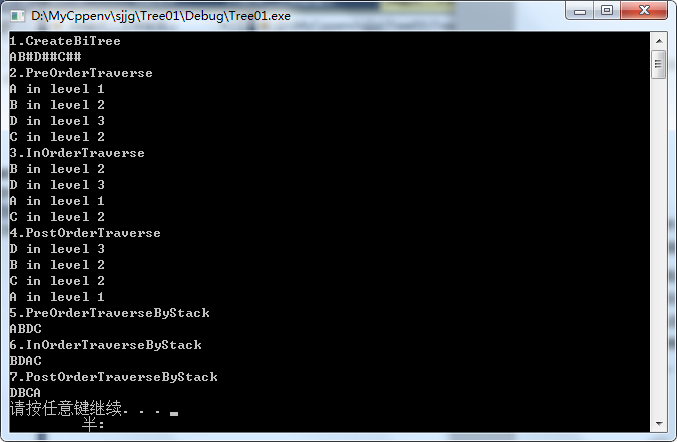
（五）使用队列完成层序遍历

#include <stdio.h>
#include <stdlib.h>
#include "BinT.h"

#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0

typedef BiTree ElemType;
typedef int Status;

//设置队列的数据结点
typedef struct QNode
{
    ElemType data;    //存放队列中的数据
    struct QNode* next;    //队列结点的指针域
}QNode, *QNodePtr;

//设置队列的结构体
typedef struct
{
    QNodePtr front, rear;    //队列头尾指针
}LinkQueue;

//四个基础操作
Status InitQueue(LinkQueue *Q);    //初始化操作，建立一个空队列Q
Status ClearQueue(LinkQueue *Q);//将队列清空
Status QueueEmpty(LinkQueue Q);    //若队列为空，返回true，否则返回false

Status EnQueue(LinkQueue *Q, ElemType e);    //若是队列存在，则插入新的元素e入队为队尾
Status DeQueue(LinkQueue *Q, ElemType *e);    //若是队列存在且非空，进行出队操作，用e接收数据

#include "queue.h"

//初始化操作，建立一个空队列Q
Status InitQueue(LinkQueue *Q)
{
    if (!Q)
        return ERROR;
    Q->front = Q->rear = (QNodePtr)malloc(sizeof(QNode));
    if (!Q->front)
        return ERROR;
    Q->front->next = Q->rear->next = NULL;
    return OK;
}


//将队列清空,保留头结点,注意队尾指针
Status ClearQueue(LinkQueue *Q)
{
    QNodePtr head = Q->front->next;    //获取开始结点
    QNodePtr cur;    //游标指针
    if (!Q)
        return ERROR;
    while (head)    //将数据全部释放
    {
        cur = head;
        head = head->next;
        free(cur);
    }
    Q->rear = Q->front;    //将队尾指向队头
    Q->rear->next = Q->front->next = NULL;    //记得：重点
    return OK;
}


//若队列为空，返回true，否则返回false
Status QueueEmpty(LinkQueue Q)
{
    if (!Q.front->next)
        return TRUE;
    return FALSE;
}


//若是队列存在，则插入新的元素e入队为队尾,注意还要考虑队尾指针
Status EnQueue(LinkQueue *Q, ElemType e)
{
    if (!Q)
        return ERROR;
    QNodePtr q = (QNodePtr)malloc(sizeof(QNode));
    if (!q)
        return ERROR;
    q->data = e;
    q->next = Q->rear->next;
    Q->rear->next = q;
    Q->rear = q;
    return OK;
}

//若是队列存在且非空，进行出队操作，用e接收数据,注意还要考虑队尾指针
Status DeQueue(LinkQueue *Q, ElemType *e)
{
    QNodePtr q;
    if (!Q || !e || QueueEmpty(*Q))
        return ERROR;
    q = Q->front->next;    //开始结点
    *e = q->data;
    Q->front->next = q->next;    //指针后移(这一步注意：重点，且易错)
    if (Q->rear == q)    //若是我们队列中只有一个结点，删除后需要修改队尾指针
        Q->rear = Q->front;
    free(q);    //释放结点
    return OK;
}

void LevelOrderTraverseByQueue(BiTree T)
{
    LinkQueue Q;
    BiTree Tmp;
    InitQueue(&Q);
    if (!T)
        return ;
    EnQueue(&Q, T);
    while (!QueueEmpty(Q))
    {
        DeQueue(&Q, &Tmp);
        printf("%c", Tmp->data);
        if (Tmp->lchild)
            EnQueue(&Q, Tmp->lchild);
        if (Tmp->rchild)
            EnQueue(&Q, Tmp->rchild);
    }
    printf("\n");
}