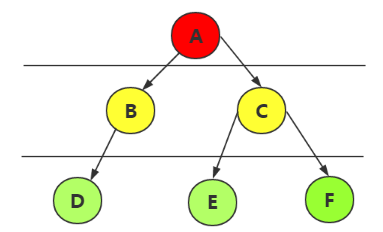
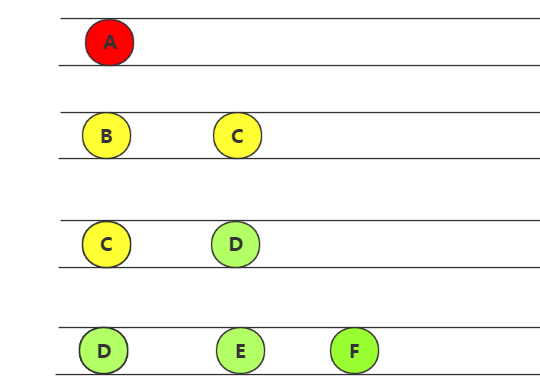
数据结构（四）树---二叉树的了解

（一）定义

二叉树(Binary Tree)是n(n>=0)个结点的有限集合,该集合或者为空集(称为空二叉树),或者有一个根节点和两颗互不相交的，方便称为根节点的左子树和右子树的二叉树组成

一般的树都可以使用孩子兄弟表示法转换为二叉树表示

（二）特殊的二叉树

1.斜二叉树

或者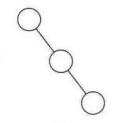

所有的结点都只有左子树的二叉树叫做左斜树
所有的结点都只有右子树的二叉树叫做右斜树
相当于链表，所以线性结构可以理解为是树的一种极其特殊的表现形式

2.满二叉树（完美二叉树）

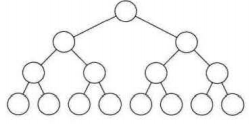
所有分支结点都存在左子树和右子树。
所有叶子结点都在同一层

3.完全二叉树

 

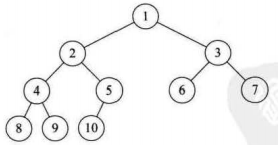
对树按照上->下，左->右，编号为i的与满二叉树中为i的位置相同

（三）二叉树的几个重要性质

性质一：第i层最大结点数位2^(i-1)个，（i>=1）

性质二：深度为k的二叉树至多有2^k-1个结点

性质三：叶结点n0与度为2的结点n2的个数关系n0=n2+1

设n1为度为1的非叶结点数
那么按照边来计算
n0+n1+n2-1    每个结点向上都有一条边指向双亲结点，除了根结点
n0*0+n1*1+n2*2    度为二，向下有2条边，度为1向下有一条边，度为0的叶子节点无下边。
两者边相等，所以得出：n0=n2+1

性质四：具有n个结点的完全二叉树的深度为[log2n]+1

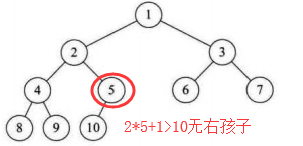
性质五：对一棵有n个结点的完全二叉树，从第一层到最大层，对任一结点i(1=<i<=n)有：

1.非根节点的父节点序号是[i/2]
2.结点（序号i）的左孩子为2i,若2i>n没有左孩子
2.结点（序号i）的右孩子为2i+1,若2i+1>n没有右孩子

（三）二叉树的存储结构

1.顺序存储（一般树很难用数组存储，但是完全二叉树可以）（从上->下，左->右顺序存储:层序存储）

使用性质五，可以快速获取双亲，左子结点，右子结点位置

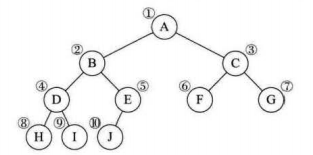
二叉树的顺序存储结构就是用一维数组存储二叉树中的结点，并且结点的存储位置，可以使用性质五来提现结点之间关系。这就是完全二叉树的优越性

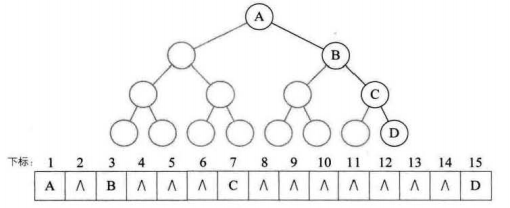
补充：对于一般二叉树也可以使用顺序存储（不过需要对空结点进行补全为^，变为一棵完全二叉树先）

我们需要结合数的结构来考虑，一棵普通的二叉树能否使用该方法。
如果是接近完全二叉树的二叉树，我们可以补全，
但是对于一棵类似于右斜二叉树，则完全没有必要，会大量浪费空间

2.二叉链表（顺序存储适用性不强，考虑使用链式存储结构）

 

//二叉树的二叉链表结点结构定义
typedef struct BiTNode    //结点结构
{
    TElemType data;    //结点数据
    struct BiTNode *lchild, *rchild;    //左右孩子指针
}BiTNode,*BiTree;

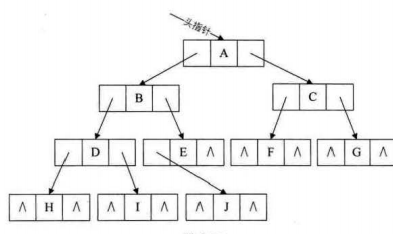
（四）二叉树的遍历（使用递归）

1.前序遍历PreOrderTraversal（根左右）

 

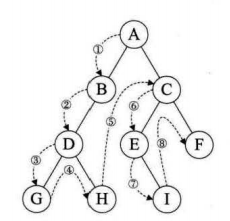
void PreOrderTraversal(BinTree BT)
{
    if (BT)
    {
        printf("%d", BT->data);
        PreOrderTraversal(BT->lchild);
        PreOrderTraversal(BT->rchild);
    }

}

2.中序遍历InOrderTraversal（左根右）

 

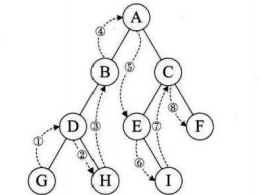
void InOrderTraversal(BinTree BT)
{
    if (BT)
    {
        InOrderTraversal(BT->lchild);
        printf("%d", BT->data);
        InOrderTraversal(BT->rchild);
    }
}

 3.后续遍历PostOrderTraversal（左右根）

 

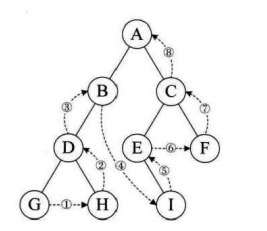
void PostOrderTraversal(BinTree BT)
{
    if (BT)
    {
        PostOrderTraversal(BT->lchild);
        PostOrderTraversal(BT->rchild);
        printf("%d", BT->data);
    }
}

4.层序遍历LevelOrderTraversal（使用顺序存储时，最便捷）

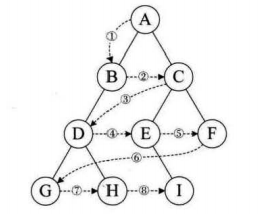
在链式二叉树中使用队列可以方便实现层序遍历

（五）二叉树的遍历（使用非递归，迭代完成）

 1.对于前，中，后序遍历，我们使用栈可以完成非递归遍历

void PreOrderTraversal(BinTree BT)
{
    BinTree T = BT;
    stack S = CreateStack(MAXSIZE);    //创建一个栈，栈空间为MAXSIZE
    while (T||!IsEmpty(S))    //当结点未遍历完，或者栈中数据未访问完
    {
        while (T)
        {
            Push(S, T);
            printf("%d", T->data);    //先将子树的最左链入栈
            T = T->lchild;
        }
        if (!IsEmpty(S))    //访问栈中节点的右子树
        {
            T = Pop(S);
            T = T->rchild;
        }
    }
}

其中中序和后序遍历只是改变打印顺序即可

2.对于层序遍历，我们使用队列来完成

void LevelOrderTraversal(BinTree BT)
{
    BinTree T = BT;
    Queue Q;
    if (!BT)
        return ERROR;
    Q = CreateQueue(MAXSIZE);    //创建一个队列，队列空间为MAXSIZE
    AddQ(Q, BT);    //将根节点先入队
    while (!IsEmpty(Q))    //当队列不为空时
    {
        T = DeleteQ(Q);    //出队一个结点
        printf("%d", T->data);    //访问数据
        if (T->lchild)
            AddQ(Q, T->lchild);    //将左孩子入队
        if (T->rchild)
            AddQ(Q, T->rchild);    //将右孩子入队
    }
}