数据结构（四）树---树的存储结构

前提

树中的某个结点的孩子可以有多个，所以仅仅使用简单的顺序结构或者链式结构是不能完全表示一整棵树的。
充分利用顺序存储结构和链式存储结构的特点，完全可以实现对树的存储结构的表示

我们表示一棵树的方法有：双亲表示法，孩子表示法，孩子兄弟表示法

补充

对于双亲表示法：我们先将双亲结点存入，我们每插入一个结点都是知道双亲结点位置的，数据可以直接插入。使用顺序存储结构更加方便
而对于孩子表示法，我们每次插入一个结点，对其子树的位置存放暂不确定，所有使用链式存储结构占主要

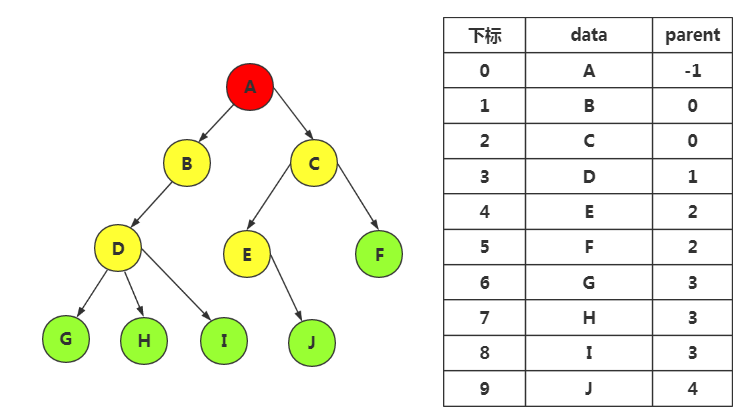
（一）双亲表示法

以双亲作为索引的关键词的一种存储方式
每个结点只有一个双亲，所以选择顺序存储占主要
以一组连续空间存储树的结点，同时在每个结点中，附设一个指示其双亲结点位置的指针域

1.结点结构 

2.结点结构定义

/*树的双亲表示法结点结构定义*/
#define MAX_TREE_SIZE 100

typedef int TElemType;

typedef struct PTNode    //结点结构
{
    TElemType data;    //结点数据
    int parent;        //双亲位置
}PTNode;

typedef struct //树结构
{
    PTNode nodes[MAX_TREE_SIZE];    //结点数组
    int r, n;    //r是根位置，n是结点数
}PTree;

 

3.优缺点分析

优点：parent指针域指向数组下标，所以找双亲结点的时间复杂度为O(1),向上一直找到根节点也快

缺点：由上向下找就十分慢，若要找结点的孩子或者兄弟，要遍历整个树

4.改进一：方便获取孩子结点

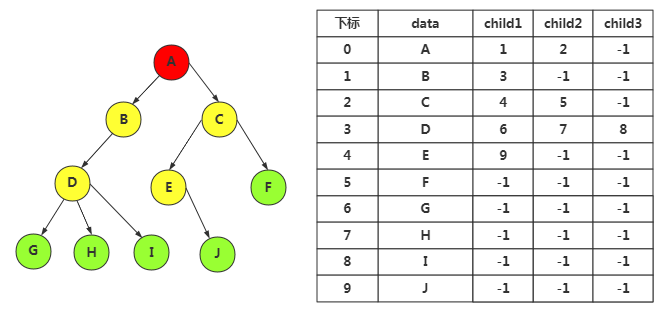
在双亲结点基础上加入孩子结点位置，由于可能一个结点有多个子树，所以我们要根据数的度来设置添加几个孩子结点的元素

 

 

树的度为3，所以我们在结点结构设置上添加3个指针域，指向孩子结点，若是孩子为空则位置为-1

/*树的双亲表示法结点结构定义*/
#define MAX_TREE_SIZE 100

typedef int TElemType;

typedef struct PTNode    //结点结构
{
    TElemType data;    //结点数据
    int parent;        //双亲位置
    int child1;        //孩子结点1
    int child2;        //孩子结点2
    int child3;        //孩子结点3
}PTNode;

typedef struct //树结构
{
    PTNode nodes[MAX_TREE_SIZE];    //结点数组
    int r, n;    //r是根位置，n是结点数
}PTree;

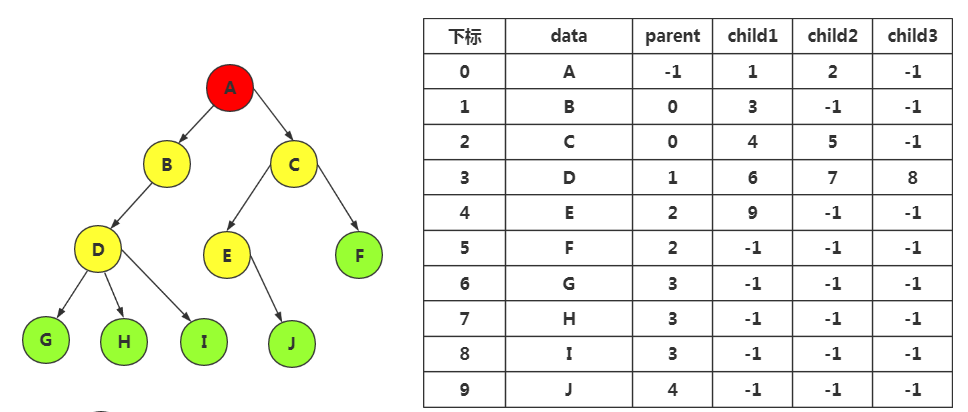
缺点：这样消耗了大量的空间，是不必要的，

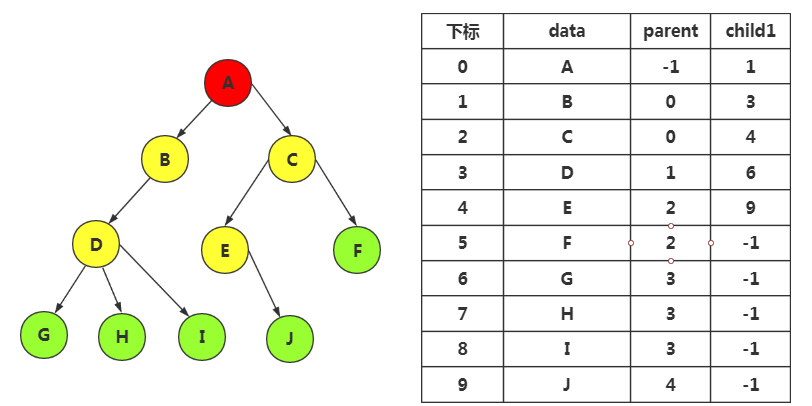
我们尽可能使用较小的空间，所以我们一般只添加一个长子域，可以获取到有0个或1个孩子结点，甚至两个子树都可以获取，但是对于较多的孩子我们若是非得使用顺序存储，就得使用上面方法。

注意：长子域是最左边孩子的域

/*树的双亲表示法结点结构定义*/
#define MAX_TREE_SIZE 100

typedef int TElemType;

typedef struct PTNode    //结点结构
{
    TElemType data;    //结点数据
    int parent;        //双亲位置
    int firstchild;    //长子域
}PTNode;

typedef struct //树结构
{
    PTNode nodes[MAX_TREE_SIZE];    //结点数组
    int r, n;    //r是根位置，n是结点数
}PTree;

 

5.改进二：方便获取各兄弟之间的关系

我们只需要增加一个有兄弟域，即可依次获取所有的兄弟结点

/*树的双亲表示法结点结构定义*/
#define MAX_TREE_SIZE 100

typedef int TElemType;

typedef struct PTNode    //结点结构
{
    TElemType data;    //结点数据
    int parent;        //双亲位置
    int rightsib;    //右兄弟结点
}PTNode;

typedef struct //树结构
{
    PTNode nodes[MAX_TREE_SIZE];    //结点数组
    int r, n;    //r是根位置，n是结点数
}PTree;

 

总结：

存储结构的设计是一个十分灵活的过程。一个存储结构设计是否合理，取决于基于该存储结构的运算是否合适，方便，时间复杂度好不好等。
例如若是我们既关注孩子又关注兄弟，而且对时间遍历要求高，那么我们可以扩展上面结构含有双亲域，长子域，右兄弟域

（二）孩子表示法（主要关注孩子结点）

由于每个结点可有多个子树（无法确定子树个数），可以考虑使用多重链表来实现。

根据树的度来设置孩子域的个数，例如本例中度为3，设置3个孩子域

/*树的孩子表示法结点结构定义*/
#define MAX_TREE_SIZE 100

typedef int TElemType;

typedef struct PTNode    //结点结构
{
    TElemType data;    //结点数据
    int child1;    //孩子1结点
    int child2;    //孩子2结点
    int child3;    //孩子3结点
}PTNode;

typedef struct //树结构
{
    PTNode nodes[MAX_TREE_SIZE];    //结点数组
    int r, n;    //r是根位置，n是结点数
}PTree;

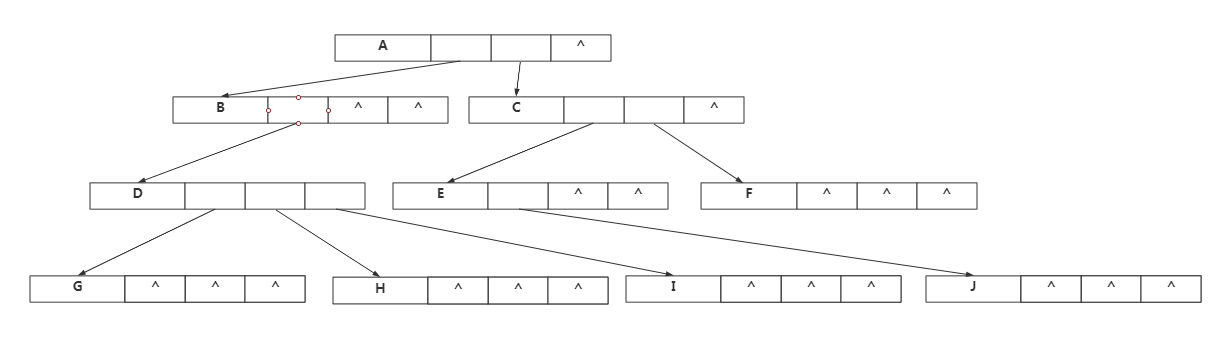
 缺点：占用了大量不必要的孩子域空指针

以其为标准：需要3n个指针域，实际上有用n-1个（除了根节点，其他n-1个都向上需要一条边），则有2n+1个无用，浪费

改进一：为每个结点添加一个结点度域，方便控制指针域的个数

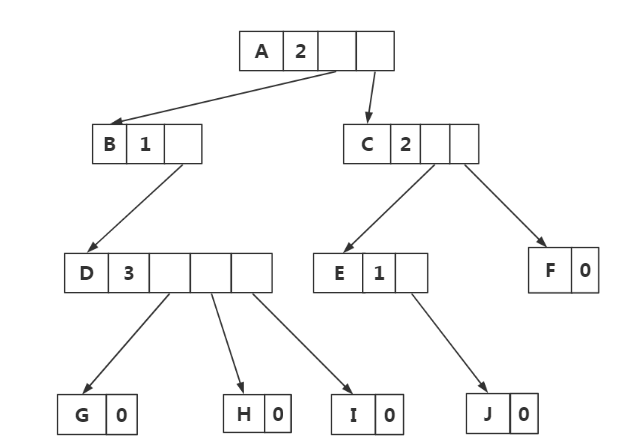
缺点：维护困难，不易实现

改进三：结合顺序结构和链式结构

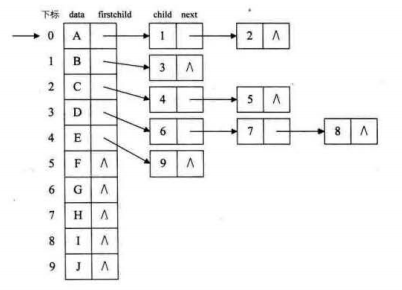
/*树的孩子表示法结点结构定义*/
#define MAX_TREE_SIZE 100

typedef int TElemType;

typedef struct CTNode    //孩子结点
{
    int child;
    struct CTNode* next;
}*ChildPtr;

typedef struct    //表头结构 
{
    TElemType data;
    ChildPtr firstChild;　　//这里只是一个头指针，指向第一个结点
}CTBox;

typedef struct //树结构
{
    CTBox nodes[MAX_TREE_SIZE];    //结点数组
    int r, n;    //r是根位置，n是结点数
}CTree;

改进四：添加双亲域，方便查找双亲结点（双亲孩子表示法）

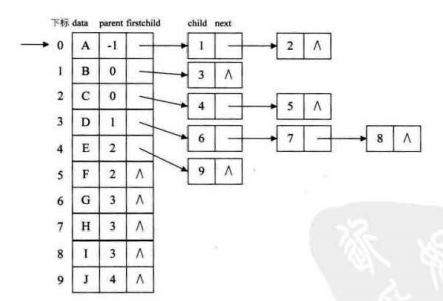
/*树的孩子表示法结点结构定义*/
#define MAX_TREE_SIZE 100

typedef int TElemType;

typedef struct CTNode    //孩子结点
{
    int child;
    struct CTNode* next;
}*ChildPtr;

typedef struct    //表头结构 
{
    TElemType data;
    int parent;
    ChildPtr firstChild;    //指向第一个孩子的指针
}CTBox;

typedef struct //树结构
{
    CTBox nodes[MAX_TREE_SIZE];    //结点数组
    int r, n;    //r是根位置，n是结点数
}CTree;

（三）孩子兄弟表示法

上面从双亲，孩子角度研究树的结构，下面我们从树的结点的兄弟角度来研究

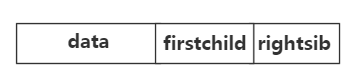
任意一棵树，他的结点的第一个孩子如果存在就是唯一结点，他的右兄弟如果存在，也是唯一的，因此，我们设置两个指针，分别指向该结点的第一个孩子和该结点的右兄弟

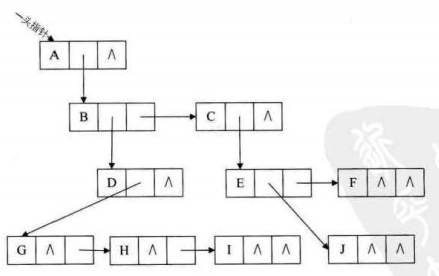
n个结点，有2n个指针域，有n-1条边，空n+1个指针域

typedef int TElemType;

typedef struct CSNode
{
    TElemType data;
    struct CSNode* firstchild, *rightsib;
}CSNode,*CSTree;

若有需要，可以再加入一个双亲域，但是上面的结构以及转换为二叉树，我们可以使用二叉树的一系列方法，来解决问题