数据结构（三）串---KMP模式匹配算法之获取next数组

（一）获取模式串T的next数组值

1.回顾

我们所知道的KMP算法next数组的作用

next[j]表示当前模式串T的j下标对目标串S的i值失配时，我们应该使用模式串的下标为next[j]接着去和目标串失配的i值进行匹配

而KMP算法的next求值函数

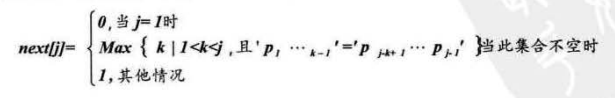
我们可以知道next除了j=1时，next[1]为0，其他情况都是比较前缀和后缀串的相似度（第三种情况是当相似度为0时，next值为0+1=1）

next数组，是用来评判前后缀的相识度，而next值，则是等于相似度加一

2.思考

虽然我们知道是比较前后缀的相似度，但是我们如何确定前后缀位置来获取next值。---->pj的next值取决于 前缀p1p2....pk-1　后缀pj-k+1.....pj-1  的相似度，next值是相似度加一

pj的next值取决于 前缀p1p2....pk-1　后缀pj-k+1.....pj-1  的相似度，是相似度加一。
我们将k-1=m,其中m就是相似度，k就是next数组值-->Max{K}
pj的next值取决于 前缀p1p2....pm　后缀pj-m.....pj-1  的相似度，是相似度加一。
那么我们现在的任务，就由找k-1变为找m，找相似度

 

例如：
虽然我们可以直接看出abab的相似度是2，
也可以编写函数获取到其相似度,
而且当我们求下一个next值时，串变为ababa，这时我们也可以看出相似度为3，使用同一个函数可以实现获取到相似度。
但是我们这个函数大概就是从头或尾开始索引，进行判断。
每次我们获取到了子串都要交给这个函数从头到尾去索引获取相似度，似乎不划算，我们是不是应该有更好的方法增加程序的性能？

 

3.下面我们尝试获取下面的T串的所有next值，从中找到关联

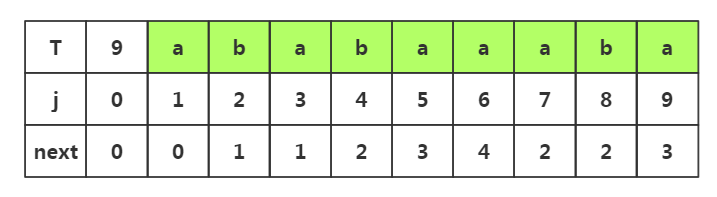
步骤一：由上一篇博文可以知道前j1,j2前两个的next是固定值为0，1

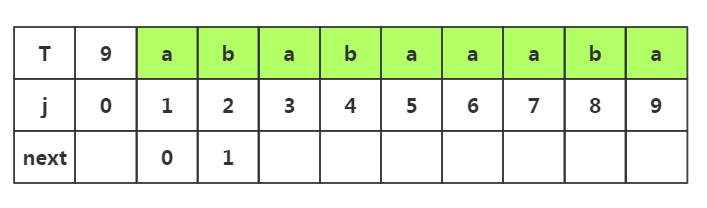
步骤二：获取j=3时的next，此时子串只有'ab'，所以子串的前缀只能选择'a',后缀只能选择'b';下面我们对前后缀进行匹配

next数组，是用来评判前后缀的相识度，而next值，则是等于相似度加一

next[j]表示当前模式串T的j下标对目标串S的i值失配时，我们应该使用模式串的下标为next[j]接着去和目标串失配的i值进行匹配

 

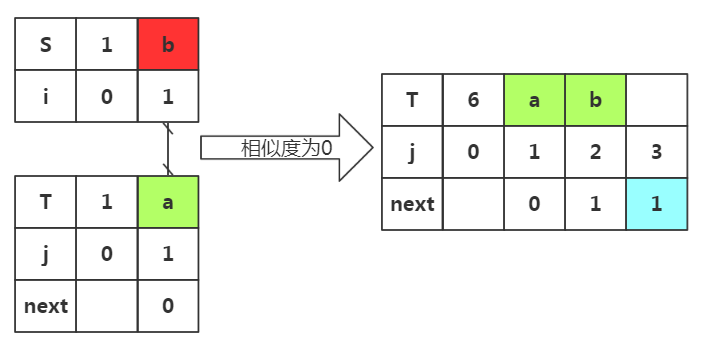
注意：匹配完毕后后缀会向下加一

步骤三：获取j=4时的next值，此时子串为'aba'，子串中前缀是p1..pm,后缀是pm+1..pj-1，若是m取一，此时子串的前缀可以选择p1，后缀选择p2;若是m=2前缀选择p1p2后缀选择p2p3;那么具体如何选择这个m值呢？

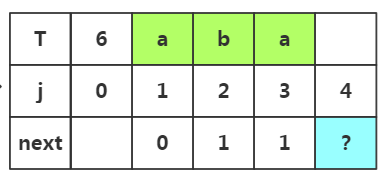
重点：这个m值取决于上次失配时的next[]值，即上次j=3是失配了，所有m=next[3]=1,所以我们选取的前缀为p1='a',后缀为pj-1是'a'

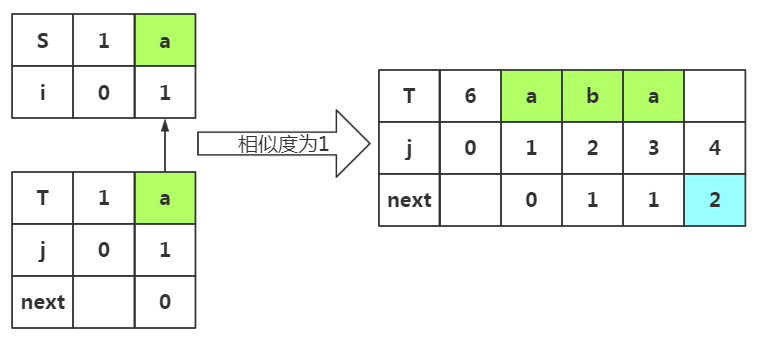
根据匹配处的相似度或者下标J=1都可以得出next[4]=2

步骤四：获取j=5时的next值，此时子串为'abab'，子串中前缀是p1..pm,后缀是pm+1..pj-1，若是m取一，此时子串的前缀可以选择p1，后缀选择p2;若是m=2前缀选择p1p2后缀选择p2p3,若m取3，前缀为p1p2p3后缀为p2p3p4;那么具体如何选择这个m值呢？

 

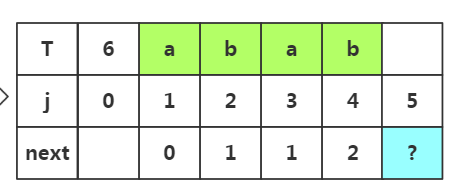
重点：若是上次匹配成功。并未失配，那么我们的m值在上一次的基础上加1。所以这次m=2,我们选取前缀p1p2和后缀p3p4

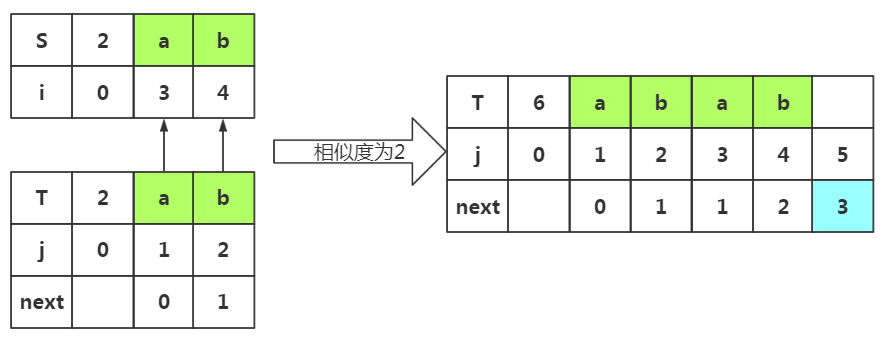
根据匹配处的相似度或者下标J=2都可以得出next[5]=3

步骤五：获取j=6时的next值，此时子串为'ababa'，子串中前缀是p1..pm,后缀是pm+1..pj-1，因为前面匹配成功，所有m++,m=3所以前缀为p1p2p3,后缀为p3p4p5

 

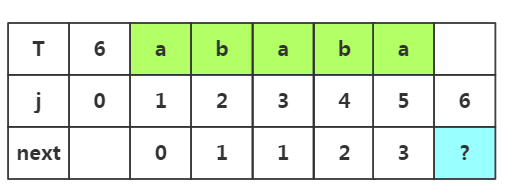
因为前面匹配成功，所有m++,m=3所以前缀为p1p2p3,后缀为p3p4p5

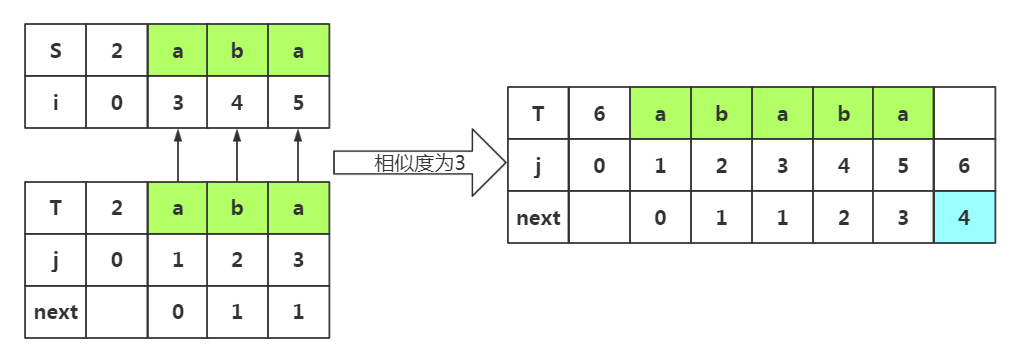
根据匹配处的相似度或者下标J=3都可以得出next[6]=4

步骤六：获取j=7时的next值，此时子串为'ababaa'，子串中前缀是p1..pm,后缀是pm+1..pj-1，因为前面匹配成功，所有m++,m=4所以前缀为p1p2p3p4,后缀为p3p4p5p6

 

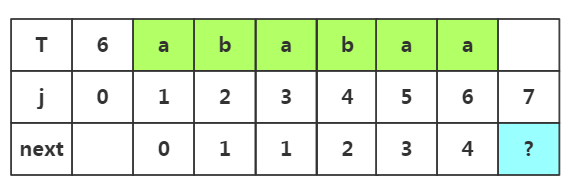
根据匹配处的相似度或者下标J=1都可以得出next[7]=2

步骤七：获取j=8时的next值，此时子串为'ababaaa'，由于上面失配了，所以m=next[7]=2,所以我们前缀为p1p2,后缀为p6p7

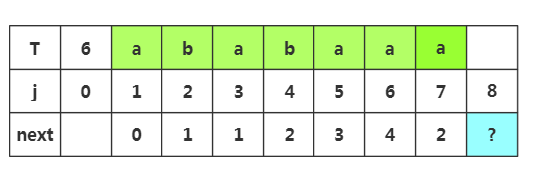
由于上面失配了，所以m=next[7]=2,匹配前缀p1p2,和后缀p6p7

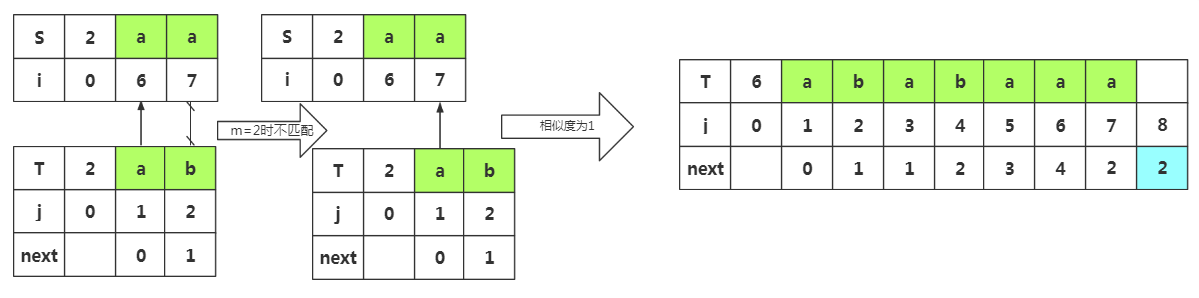
根据匹配处的相似度或者下标J=1都可以得出next[8]=2

步骤七：获取j=9时的next值，此时子串为'ababaaab'，由于上面失配了，所以m=next[8]=2,所以我们前缀为p1p2,后缀为p7p8

 

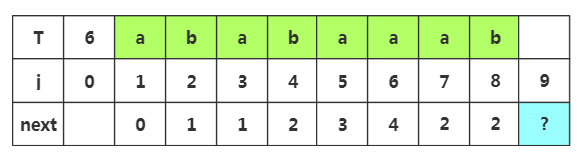
由于上面失配了，所以m=next[8]=2,所以我们前缀为p1p2,后缀为p7p8

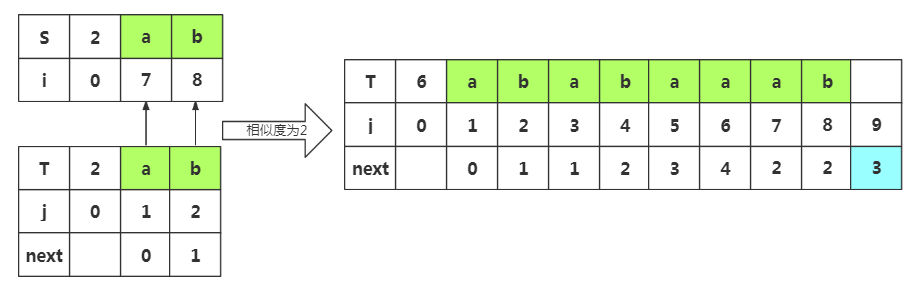
根据匹配处的相似度或者下标J=2都可以得出next[9]=3

另一种方案：是直接看匹配位置的j值即可，将j值加一即可，这个是实现程序的时候的使用思路

注意：有可能模式串只有一个字符进行匹配，那么我们之前说的next[2]=1也需要我们去匹配一遍，而不是直接获取结果

重点补充：为什么我们可以使用下标值j来表示相似度？

我们以上图为例：
相似度是指前缀串和后缀串之间的相似程度，通过看图，我们不难发现相似度和最后匹配的下标使一样的。
这是因为前缀始终是以下标为一的字符开始匹配，所以匹配到下标为多少，那他的相似度就是多少

4.代码实现

//通过计算返回子串T的next数组
void get_next(String T, int* next)
{
    int m, j;
    j = 1;    //j是后缀的末尾下标　　　　　　pj-m...pj-1　　其实j-1就是后缀的下标，而j就是我们要求的next数组下标
    m = 0;    //m代表的是前缀结束时的下标，也就是相似度，是等价的　　p1p2...pm
    next[1] = 0;
    while (j < T[0])　　//T[0]是表示串T的长度
    {
　　　　 //这个if,我们只需要考虑，如果我<后缀最后下标>前面匹配成功，现在我T[j]==T[m]也匹配成功，那么我对应的next<++j>数组值是多少？
        if (m == 0 || T[m] == T[j])    //T[m]表示前缀的最末尾字符，T[j]是后缀的最末尾字符
        {
            ++m;
            ++j;
            next[j] = m;　　//++j后获取的才是我们要的next[j]下标，我们要获取next[j]处的值，就是获取他前一个匹配时的相似度，也就是前一个匹配的下标+1
        }
        else　　//else是匹配失败的情况，就要进行回溯
            m = next[m];    //若是字符不相同，则m回溯
    }
}

5.测试结果

int main()
{
    int i;
    String s1;
    int next[MAXSIZE] = { 0 };
    char *str = (char*)malloc(sizeof(char) * 40);
    memset(str, 0, 40);
    printf("enter s1:");
    scanf("%s", str);
    if (!StrAssign(s1, str))
        printf("1.string length is gt %d\n", MAXSIZE);
    else
        printf("1.string StrAssign success\n");

    get_next(s1, next);

    for (i = 1; i <= StringLength(s1); i++)
        printf("%d ", next[i]);
    system("pause");
    return 0;
}