(一)汉罗塔的了解
大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。
(二)拆分小块,分治思想
只有3个圆盘时



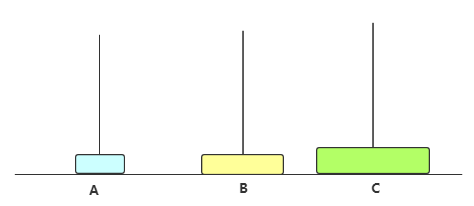
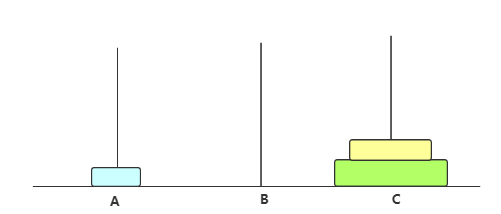
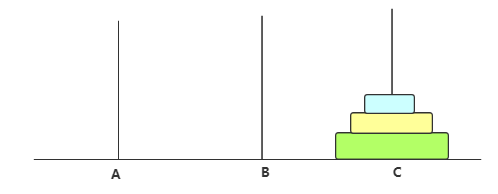
步骤总结
Hanoi(n,A,B,C)将n个圆盘从A移动到C,经过B
最开始:需要移动的圆盘n都在A柱上
1.将A柱的碍事圆盘n-1个经过C,移动到B Hanoi(n-1,A,C,B)
2.将A中唯一最大圆盘移动到C move(n,A,C)
3.将B中的所有圆盘使用同样的方法移动到C中 Hanoi(n-1,B,A,C)
一次操作,将所有需要移动的圆盘n-1放到B柱上 同样将
所有我们可以进行下一次递归了
(三)代码实现
int count;
void move(int n, char q, char p)
{
count++;
printf("%d times Move %d: Move from %c to %c\n", count, n, q, p);
}
void Hanoi(int n, char a, char b, char c) //函数定义:将n个圆盘,由柱a经过柱b移动到目标柱c
{
if (n == 1)
move(n, a, c); //若是只有一个圆盘,直接移动到目标柱中
else
{
Hanoi(n - 1, a, c, b); //将a上面的n-1个圆盘经过c移动到b中
move(n, a, c); //将剩下的一个最大圆盘从a移动到c
Hanoi(n - 1, b, a, c); //同样的想法将b中的n-1个圆盘移动到c中
}
}
int main()
{
int n = 3;
Hanoi(n, 'X', 'Y', 'Z');
system("pause");
return 0;
}
int main()
{
int n = 3;
Hanoi(n, 'X', 'Y', 'Z');
system("pause");
return 0;
}

int main()
{
int n = 4;
Hanoi(n, 'X', 'Y', 'Z');
system("pause");
return 0;
}

(四)解析
1.假设移动n个圆盘从A柱到B柱的次数为H(n)
2.先把n-1个盘子从A柱移动到B柱,则需要移动的次数为H(n-1)
3.再把最大的那个圆盘从A柱移动到C柱需要一次
4.再把n-1个圆盘从B柱移动到C柱需要H(n-1)
5.由此可以得出
当n=1时,H(1)=1;
当n>1时,H(n)=2*H(n-1)+1;
6.由5得出H(n)=2^n-1 (n>0)
(五)总结
递归写起来简单,想起来有点烧脑....
汉罗塔移动:
1.柱A中有n个圆盘需要移动到目标柱C中
2.将柱A上的n-1个圆盘移动到目标柱B中
3.将柱A中最后1个圆盘移动到目标柱C中
4.将柱B中的n-1个圆盘移动到目标柱C中
注:目标柱在函数中是会变的,不过我们调用的最终目标柱是C
由上面四个步骤可以知道,移动到目标柱的规律是一样的。所以我们定义一个函数用来将所有需要移动的圆盘移动到目标柱上
void Hanoi(int n, char a, char b, char c)
现在使用函数来说明步骤
1.Hanoi(n, 'X', 'Y', 'Z'); 将n个圆盘由a=X柱移动到c=Z柱
2.Hanoi(n - 1, a, c, b); 将柱A上的n-1个圆盘移动到目标柱B中
3.move(n, a, c); 将柱A中最后1个圆盘移动到目标柱C中
4.Hanoi(n - 1, b, a, c) 将柱B中的n-1个圆盘移动到目标柱C中
move(n, a, c); //是不是真正移动了某个圆盘,我们只是去打印出来










