数据结构(二)栈与队列---栈的应用(递归和分治思想)
(一)递归定义
我们把一个直接调用自己活着通过一系列的调用语句间接的调用自己的函数,称做递归函数。
一般,若是我们知道循环的次数,就不要使用递归,使用迭代同样可以实现。而且递归效率太低。使用不多。
另外:递归实现要比迭代简单明了。
(二)斐波那契数列实现
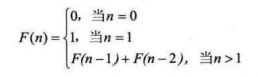

#define _CRT_SECURE_NO_WARNINGS #include <stdio.h> #include <stdlib.h> int main() { int i; int a[40]; a[0] = 0; a[1] = 1; printf("%d ", a[0]); printf("%d ", a[1]); for (i = 2; i < 40;i++) { a[i] = a[i - 1] + a[i - 2]; printf("%d ", a[i]); } system("pause"); return 0; }
#define _CRT_SECURE_NO_WARNINGS #include <stdio.h> #include <stdlib.h> int Fbi(int i) { if (i<2) return i == 0 ? 0 : 1; return Fbi(i - 1) + Fbi(i - 2); } int main() { int i; for (i = 0; i < 40; i++) printf("%d ", Fbi(i)); system("pause"); return 0; }
(三)递归和迭代性能比较
通过上面斐波那契数列,当我们的求取的数越大,发现使用递归获取结果的时间越长。而对于迭代影响几乎不计
迭代
for (i = 2; i < 40;i++) { a[i] = a[i - 1] + a[i - 2]; printf("%d ", a[i]); }
对于迭代的时间复杂度是O(n)----->当n小的时候几乎速度可以达到O(1)十分快
递归
int Fbi(int i) { if (i<2) //每个递归必须定义至少一个条件,当满足这个条件不再进行 return i == 0 ? 0 : 1; return Fbi(i - 1) + Fbi(i - 2); }
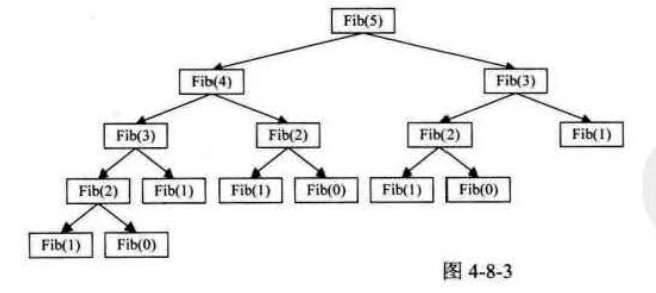
所用的时间复杂度几乎是O(2^n),而且还不含出栈入栈等操作消耗的时间,已经是一个十分恐怖的耗时操作
(四)实例体现递归的简单性-----将输入的任意长字符串反向输出
可以使用栈:但是太麻烦,不如递归简单
void printStr() { char a; scanf("%c", &a); if (a == '#') return printf("%c", a); printStr(); printf("%c", a); }
(五)分治思想(分而治之)
分治思想在算法中非常常见,当一个问题规模较大且不易求解时,就可以考虑将问题分为几个较小的模块。逐一解决。
分治思想和递归是相同的,因为采用分治思想处理问题,其各个小模块通常具有与大问题相同的结构,这种特性也使递归技术有了用武之地
折半查找算法的递归实现(二分查找)
折半查找法,是一种常用的查找方法,该方法通过不断缩小一半查找的范围,直到达到目的,所以效率比较高
前提:针对有序数组(元素从小到大或从大到小)
优点:查询速度较快,时间复杂度为

缺点:有硬性条件的限制,而且即使查到后,插入与删除困难。
下面查找27这个数
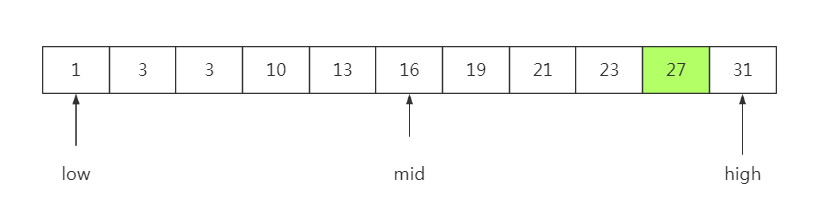
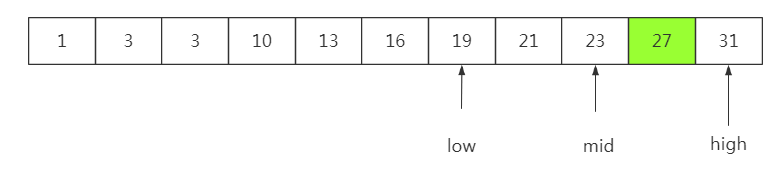

迭代
int main() { int a[11] = { 1, 3, 3, 10, 13, 16, 19, 21, 23, 27, 31 }; int left, mid, right,num; left = 0; right = 10; num = 27; while (left <= right) { mid = (left + right) / 2; if (a[mid] > num) right = mid - 1; else if (a[mid] < num) left = mid + 1; else break; } printf("index:%d", mid); system("pause"); return 0; }

递归
int binary_search(int arr[], int left, int right,int ele) { int mid = (left + right) / 2; if (arr[mid] > ele) right = mid - 1; else if (arr[mid] < ele) left = mid + 1; else return mid; return binary_search(arr, left, right, ele); } int main() { int a[11] = { 1, 3, 3, 10, 13, 16, 19, 21, 23, 27, 31 }; int left, right, num, index; left = 0; right = 10; num = 27; index = binary_search(a, left, right, num); printf("index:%d", index); system("pause"); return 0; }





