数据结构(二)栈与队列---栈的应用:四则运算实现
栈的应用:四则运算实现
注:我们这里使用链栈来实现,当然前面的顺序栈同样可以实现,而且更加容易理解。这里我们使用链栈来练习
(一)预备知识
前缀、中缀、后缀表达式(逆波兰表达式)
union联合体使用详解
前缀表达式、中缀表达式、后缀表达式都是四则运算的表达方式,用以四则运算表达式求值
中缀表达式
中缀表达式就是常见的运算表达式,如(3+4)×5-6
前缀表达式
前缀表达式又称波兰式,前缀表达式的运算符位于操作数之前
比如:- × + 3 4 5 6
后缀表达式(逆波兰表达式)<这是我们使用的>
后缀表达式又称逆波兰表达式,与前缀表达式相似,只是运算符位于操作数之后
比如:3 4 + 5 × 6 -
(二)中缀转后缀
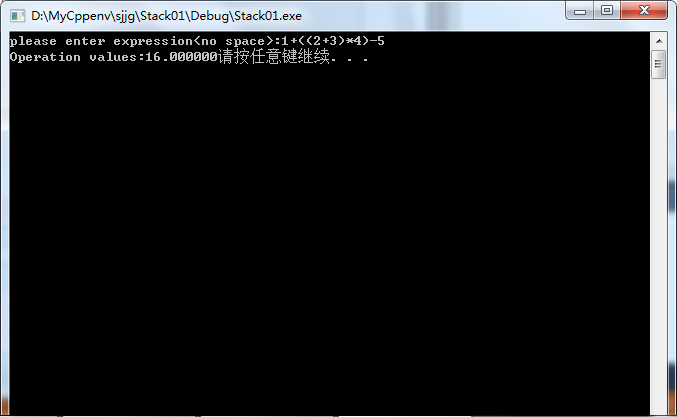
例如,将中缀表达式“1+((2+3)×4)-5”转换为后缀表达式的过程如下:
| 扫描到的元素 | s2(栈底->栈顶) | s1 (栈底->栈顶) | 说明 |
|---|---|---|---|
| 1 | 1 | 空 | 数字,直接入栈 |
| + | 1 | + | s1为空,运算符直接入栈 |
| ( | 1 | + ( | 左括号,直接入栈 |
| ( | 1 | + ( ( | 同上 |
| 2 | 1 2 | + ( ( | 数字 |
| + | 1 2 | + ( ( + | s1栈顶为左括号,运算符直接入栈 |
| 3 | 1 2 3 | + ( ( + | 数字 |
| ) | 1 2 3 + | + ( | 右括号,弹出运算符直至遇到左括号 |
| × | 1 2 3 + | + ( × | s1栈顶为左括号,运算符直接入栈 |
| 4 | 1 2 3 + 4 | + ( × | 数字 |
| ) | 1 2 3 + 4 × | + | 右括号,弹出运算符直至遇到左括号 |
| - | 1 2 3 + 4 × + | - | -与+优先级相同,因此弹出+,再压入- |
| 5 | 1 2 3 + 4 × + 5 | - | 数字 |
| 到达最右端 | 1 2 3 + 4 × + 5 - | 空 | s1中剩余的运算符 |
因此结果为“1 2 3 + 4 × + 5 -”
步骤:
- 初始化两个栈:运算符栈s1和储存中间结果的栈s2;
- 从左至右扫描中缀表达式;
- 遇到操作数时,将其压s2;
- 遇到运算符时,比较其与s1栈顶运算符的优先级:
- 如果s1为空,或栈顶运算符为左括号“(”,则直接将此运算符入栈;
- 否则,若优先级比栈顶运算符的高,也将运算符压入s1(注意转换为前缀表达式时是优先级较高或相同,而这里则不包括相同的情况);
- 否则,将s1栈顶的运算符弹出并压入到s2中,再次转到(4-1)与s1中新的栈顶运算符相比较;
- 遇到括号时:
- 如果是左括号“(”,则直接压入s1;
- 如果是右括号“)”,则依次弹出s1栈顶的运算符,并压入s2,直到遇到左括号为止,此时将这一对括号丢弃;
- 重复步骤2至5,直到表达式的最右边;
- 将s1中剩余的运算符依次弹出并压入s2;
- 依次弹出s2中的元素并输出,结果的逆序即为中缀表达式对应的后缀表达式(转换为前缀表达式时不用逆序)
(三)计算后缀表达式结果
从左至右扫描表达式,遇到数字时,将数字压入堆栈,遇到运算符时,弹出栈顶的两个数,用运算符对它们做相应的计算(次顶元素 op 栈顶元素),并将结果入栈;重复上述过程直到表达式最右端,最后运算得出的值即为表达式的结果
例如后缀表达式“3 4 + 5 × 6 -”:
- 从左至右扫描,将3和4压入堆栈;
- 遇到+运算符,因此弹出4和3(4为栈顶元素,3为次顶元素,注意与前缀表达式做比较),计算出3+4的值,得7,再将7入栈;
- 将5入栈;
- 接下来是×运算符,因此弹出5和7,计算出7×5=35,将35入栈;
- 将6入栈;
- 最后是-运算符,计算出35-6的值,即29,由此得出最终结果。
(四)代码实现
//栈中数据类型 typedef struct Data { int flag; //1为字符,2为浮点数 union { double num; char sign; }number; }data;

#define _CRT_SECURE_NO_WARNINGS #include <stdio.h> #include <stdlib.h> #define OK 1 #define ERROR 0 #define TRUE 1 #define FALSE 0 #define STACK_INIT_SIZE 100 //定义栈的初始大小 #define STACK_INCR_SIZE 10 //定义栈的增长大小 #define MAXSIZE 100 //中缀表达式的长度 typedef struct Data { int flag; //1为字符,2为浮点数 union { double num; char sign; }number; }data; typedef data ElemType; typedef int Status; typedef struct { ElemType *base; //栈底指针 ElemType *top; //栈顶指针 int stackSize; //最大容量,这是可修改的 }sqStack; //四个基础操作 Status InitStack(sqStack *s); //初始化操作,建立一个空栈 Status ClearStack(sqStack *s); //将栈清空 Status StackEmpty(sqStack s); //若栈存在,返回true,否则返回false int StackLength(sqStack s); //返回栈S的元素个数 Status GetTop(sqStack s, ElemType *e); //若是栈存在且非空,用e返回S的栈顶元素 Status Push(sqStack *s, ElemType e); // 若是栈存在,则插入新的元素e到栈S中并成为栈顶元素 Status Pop(sqStack *s, ElemType *e); //若是栈存在且非空,删除栈顶元素,并用e返回其值 Status DestroyStack(sqStack *s); //若是栈存在,则销毁他 void PrintStack(sqStack s); //打印所有数据,测试用,会依次将数据出栈 //初始化操作,建立一个空栈 Status InitStack(sqStack *s) { s->base = (ElemType *)malloc(STACK_INIT_SIZE*sizeof(ElemType)); if (!s->base) return ERROR; s->top = s->base; //最开始,栈顶就是栈底 s->stackSize = STACK_INIT_SIZE; return OK; } //将栈清空,将栈顶指针移动到栈底即可,容量大小不要修改,数据不需要清空,数据入栈会覆盖 Status ClearStack(sqStack *s) { if (s == NULL) return ERROR; s->top = s->base; return OK; } //若栈存在,返回true,否则返回false Status StackEmpty(sqStack s) { if (s.base == s.top) return TRUE; return FALSE; } //返回栈S的元素个数 int StackLength(sqStack s) { int length = s.top - s.base; //指针之间运算,是按照其中数据大小字节来算的 return length; } //若是栈存在且非空,用e返回S的栈顶元素,注意:只是获取栈顶数据,不出栈 Status GetTop(sqStack s, ElemType *e) { if (!e || StackEmpty(s) || !s.base) return ERROR; *e = *(s.top - 1); return OK; } //入栈操作:若是栈存在,则插入新的元素e到栈S中并成为栈顶元素 Status Push(sqStack *s, ElemType e) { ElemType* newStack; if (!s->base) return ERROR; if (s->top-s->base>=s->stackSize) //栈满,需要再分配 { newStack = (ElemType *)realloc(s->base, (s->stackSize + STACK_INCR_SIZE)*sizeof(ElemType)); //重新分配大小 if (!newStack) //若是分配失败,会返回NULL { free(s->base); exit(0); //分配失败,直接退出 } s->base = newStack; //分配后需要将栈顶指针进行移动到新的位置 s->top = s->base + s->stackSize; } *(s->top) = e; s->top++; return OK; } //若是栈存在且非空,删除栈顶元素(只需要将栈顶指针下移即可),并用e返回其值 Status Pop(sqStack *s, ElemType *e) { if (!s->base || !e || StackEmpty(*s)) return ERROR; *e = *(--s->top); return OK; } //若是栈存在,则销毁他(直接将栈底指针释放即可,置为空) Status DestroyStack(sqStack *s) { if (!s->base) //若是栈存在 { s->stackSize = 0; free(s->base); s->base = s->top = NULL; } return OK; } //打印数据 void PrintStack(sqStack s) { data d; int len = StackLength(s); for (int i = 0; i < len;i++) { Pop(&s, &d); if (d.flag == 1) printf("%c", d.number.sign); else printf("%lf", d.number.num); } }
//四则运算需要的函数 Status MatchBrack(char* str); //匹配括号是否正确 Status RotateStack(sqStack* s); //将栈中的数据翻转 Status GetMidStack(sqStack *s, char* str); //获取中缀表达式,将字符串转换到栈中 Status GetBackStack(sqStack *s); //获取后缀表达式 Status GetBackValue(sqStack *s, double* val); //获取后缀表达式计算出来的结果
//括号匹配 Status MatchBrack(char* str) { char *cur = str; sqStack BrkSK; data d; char ch; Status sta = OK;; if (!str || !InitStack(&BrkSK)) return ERROR; while (*cur!='\0') { if (*cur=='('||*cur=='['||*cur=='{') { d.flag = 1; d.number.sign = *cur; Push(&BrkSK,d); } else if (*cur == ')' || *cur == ']' || *cur == '}' ) { if (!GetTop(BrkSK, &d)) { sta = ERROR; break; } ch = d.number.sign; if ((*cur == ')'&&ch == '(') || (*cur == ']'&&ch == '[') || (*cur == '}'&&ch == '{')) Pop(&BrkSK, &d); else { sta = ERROR; break; } } cur++; } DestroyStack(&BrkSK); return sta; } //获取中缀表达式 Status GetMidStack(sqStack *s, char* str) { char* cur, *start, *end; cur = start = end = str; char fnum[10] = { 0 }; data d; if (!s || !str) return ERROR; while (*cur != '\0') { if (!isdigit(*cur) && *cur != '.') { if (cur > str&&isdigit(*(cur - 1))) { end = cur; memset(fnum, 0, 10); memcpy(fnum, start, (end - start)); d.flag = 2; d.number.num = atof(fnum); Push(s, d); } d.flag = 1; d.number.sign = *cur; if (isdigit(*(cur + 1))) start = cur + 1; Push(s, d); } cur++; } if (start > end) //最后以数字结尾,需要再进行判断 { end = cur; memset(fnum, 0, 10); memcpy(fnum, start, (end - start)); d.flag = 2; d.number.num = atof(fnum); Push(s, d); } return OK; } //将栈中的数据翻转 Status RotateStack(sqStack* s) { sqStack tempSk, *freeSk; if (!InitStack(&tempSk) || !s) return ERROR; data d; int length = StackLength(*s); for (int i = 0; i < length; i++) { Pop(s, &d); Push(&tempSk, d); } freeSk = s; *s = tempSk; DestroyStack(freeSk); } //获取后缀表达式 Status GetBackStack(sqStack *s) { sqStack OperaSk, ResSk, *tempSk; OperaSk.base = ResSk.base = NULL; data d, top; char pc; //存储单个运算符 int length = StackLength(*s); if (!s) return ERROR; if (!InitStack(&OperaSk) || !InitStack(&ResSk)) { DestroyStack(&OperaSk); DestroyStack(&ResSk); return ERROR; } for (int i = 0; i < length; i++) { Pop(s, &d); if (d.flag == 2) Push(&ResSk, d); if (d.flag == 1) { if (GetTop(OperaSk, &top)) pc = top.number.sign; if (d.number.sign == ')') { //将'('之上的运算符全部弹出到ResSk while (pc != '(') { Pop(&OperaSk, &d); Push(&ResSk, d); GetTop(OperaSk, &top); pc = top.number.sign; } Pop(&OperaSk, &d); //将(一起弹出 continue; } if (StackEmpty(OperaSk) || pc == '(' || d.number.sign == '(') //若是OperaSk为空或者栈顶为(或者获取的运算符为(,我们直接将这个运算符压栈 Push(&OperaSk, d); else if ((pc == '-' || pc == '+') && (d.number.sign == '*' || d.number.sign == '/')) //若是栈顶的优先级低,也压栈,但是要先将栈顶的 Push(&OperaSk, d); else if (pc == d.number.sign || (pc == '-'&&d.number.sign == '+') || (pc == '+'&&d.number.sign == '-') || (pc == '*'&&d.number.sign == '/') || (pc == '/'&&d.number.sign == '*')) //当栈顶优先级和当前运算符一致,先弹出到ResSk,在进行压栈 { Pop(&OperaSk, &top); Push(&ResSk, top); Push(&OperaSk, d); } else //当获取的运算符优先级低于栈顶优先级,先将栈顶运算符移栈到ResSk,然后再将当前运算符与下一次进行比较,压栈到OperaSK栈 { Pop(&OperaSk, &top); //获取OperaSK栈顶数据 Push(&ResSk, top); //将数据放入ResSK栈 Push(s, d); //由于当前数据没有完成入栈,我们将它放回原来栈中,再次进行比较 length++; } } } while (!StackEmpty(OperaSk)) //将运算符栈中的剩余的数据全部移到结果栈 { Pop(&OperaSk, &d); Push(&ResSk, d); } tempSk = s; *s = ResSk; DestroyStack(tempSk); DestroyStack(&OperaSk); return OK; } //获取后缀表达式计算出来的结果 Status GetBackValue(sqStack *s, double* val) { sqStack OpValSk; //获取运算结果的栈 int length = StackLength(*s); double op1, op2, value = 0; data d, top; if (!s || !InitStack(&OpValSk)) return ERROR; for (int i = 0; i < length; i++) { Pop(s, &d); if (d.flag == 2) //数字 Push(&OpValSk, d); else //运算符,取两个数运算后,放回栈中 { Pop(&OpValSk, &top); op2 = top.number.num; Pop(&OpValSk, &top); op1 = top.number.num; switch (d.number.sign) { case '+': value = op1 + op2; break; case '-': value = op1 - op2; break; case '*': value = op1 * op2; break; case '/': value = op1 / op2; break; default: break; } d.flag = 2; d.number.num = value; Push(&OpValSk, d); } } *val = value; DestroyStack(&OpValSk); return OK; }
int main() { sqStack sk; double value; ElemType e; char str[MAXSIZE] = { 0 }; sk.base = sk.top = NULL; //用于判断是否存在 //初始化空栈 InitStack(&sk); //接收输入的中缀表达式 printf("please enter expression<no space>:"); scanf("%s", str); //先进行括号匹配 if (!MatchBrack(str)) return 0; //将字符串中的中缀表达式分割,转换为中缀表达式存放在栈中'1+2+3'--->3.0 + 2.0 + 1.0每一个都是一个栈空间数据 GetMidStack(&sk, str); //将上面的中缀表达式翻转,变为正常的 RotateStack(&sk); //下面将中缀表达式转后缀表达式 GetBackStack(&sk); //将上面的后缀表达式翻转,变为正常的 RotateStack(&sk); //获取后缀表达式结果 GetBackValue(&sk, &value); //PrintStack(sk); printf("Operation values:%lf", value); //PrintStack(sk); DestroyStack(&sk); system("pause"); return 0; }
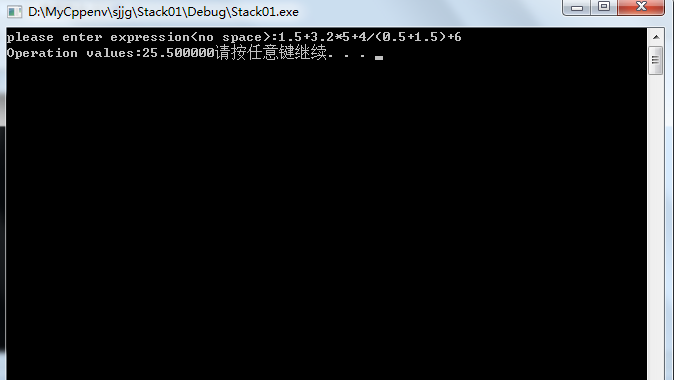
(五)结果演示
(六)反思
实现了小数运算,但是不足的是对方法不熟悉,导致耗费太多时间



