(一)前提
通常我们使用栈的顺序存储结构来存储,栈的链式存储我们了解思想即可,进行扩展
栈因为只是栈顶来做插入和删除操作,所以比较好的方法就是将栈顶放在单链表的头部,栈顶指针和单链表的头指针合二为一
(二)链式存储结构
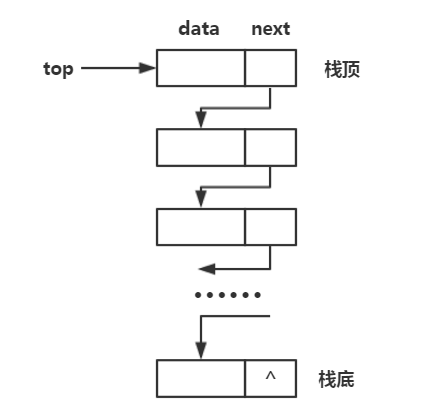
注意:由于栈顶是在开始结点,会一直变化,我们不需要设置头结点
(三)链栈的结构体
//设置链栈的结点
typedef struct StackNode
{
ElemType data; //存放栈中的数据
struct StackNode* next; //单链表的指针域
}StackNode,*LinkStackPtr;
//设置栈的结构体
typedef struct
{
LinkStackPtr top; //top指针,始终与头指针保持一致
int count; //栈元素计数器
}LinkStack;
(四)链栈的代码实现
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define STACK_INIT_SIZE 100 //定义栈的初始大小
#define STACK_INCR_SIZE 10 //定义栈的增长大小
typedef int ElemType;
typedef int Status;
//设置链栈的结点
typedef struct StackNode
{
ElemType data; //存放栈中的数据
struct StackNode* next; //单链表的指针域
}StackNode,*LinkStackPtr;
//设置栈的结构体
typedef struct
{
LinkStackPtr top; //top指针,始终与头指针保持一致
int count; //栈元素计数器
}LinkStack;
//四个基础操作
Status InitStack(LinkStack *s); //初始化操作,建立一个空栈
Status ClearStack(LinkStack *s); //将栈清空
Status StackEmpty(LinkStack s); //若栈存在,返回true,否则返回false
int StackLength(LinkStack s); //返回栈S的元素个数
Status GetTop(LinkStack s, ElemType *e); //若是栈存在且非空,用e返回S的栈顶元素
Status Push(LinkStack *s, ElemType e); // 若是栈存在,则插入新的元素e到栈S中并成为栈顶元素
Status Pop(LinkStack *s, ElemType *e); //若是栈存在且非空,删除栈顶元素,并用e返回其值
Status DestroyStack(LinkStack *s); //若是栈存在,则销毁他
int main()
{
LinkStack sk;
ElemType e;
int i;
//初始化空栈,用于存放()[]{}''""这几个数据,的左半边进行匹配
InitStack(&sk);
printf("2.Push 1-5\n");
for (i = 1; i <= 5; i++)
Push(&sk, i);
printf("3.Pop number for three times\n");
for (i = 1; i <= 3;i++)
{
Pop(&sk, &e);
printf("Pop %d: %d\n",i, e);
}
GetTop(sk, &e);
printf("4.Get Top:%d\n",e);
printf("5.Push 6-10\n");
for (i = 6; i <= 10; i++)
Push(&sk, i);
printf("6.Get stack length:%d\n", StackLength(sk));
printf("7.Pop number for six times\n");
for (i = 1; i <= 6; i++)
{
Pop(&sk, &e);
printf("Pop %d: %d\n",i, e);
}
if (!StackEmpty(sk))
{
printf("8.Stack is not Empty\n");
ClearStack(&sk);
printf("9.Stack is Clear\n");
}
printf("10.Stack Empty:%d\n",StackEmpty(sk));
printf("11.destroy Stack");
DestroyStack(&sk);
system("pause");
return 0;
}
//初始化操作,建立一个空栈
Status InitStack(LinkStack *s)
{
if (!s)
return ERROR;
s->count = 0;
s->top = NULL;
return OK;
}
//将栈清空,循环释放掉栈中的结点
Status ClearStack(LinkStack *s)
{
LinkStackPtr p, q; //结点指针
if (s == NULL)
return ERROR;
p = s->top;
while (p)
{
q = p;
p = p->next;
free(q);
}
s->count = 0;
s->top=NULL;
return OK;
}
//若栈存在,返回true,否则返回false
Status StackEmpty(LinkStack s)
{
if (s.count==0)
return TRUE;
return FALSE;
}
//返回栈S的元素个数
int StackLength(LinkStack s)
{
return s.count;
}
//若是栈存在且非空,用e返回S的栈顶元素,注意:只是获取栈顶数据,不出栈
Status GetTop(LinkStack s, ElemType *e)
{
if (!e || !s.top)
return ERROR;
*e = s.top->data;
return OK;
}
//入栈操作:若是栈存在,则插入新的元素e到栈S中并成为栈顶元素
Status Push(LinkStack *s, ElemType e)
{
if (!s)
return ERROR;
LinkStackPtr ns = (LinkStackPtr)malloc(sizeof(StackNode)); //生成一个结点去存放数据
ns->data = e;
ns->next = s->top;
s->top = ns;
s->count++;
return OK;
}
//若是栈存在且非空,删除栈顶元素(只需要将栈顶指针下移即可),并用e返回其值
Status Pop(LinkStack *s, ElemType *e)
{
LinkStackPtr p;
if (!s || !e||StackEmpty(*s))
return ERROR;
p = s->top;
s->top = p->next;
*e = p->data;
free(p);
s->count--;
return OK;
}
//若是栈存在,则销毁他(直接将栈底指针释放即可,置为空)
Status DestroyStack(LinkStack *s)
{
if (!StackEmpty(*s)) //若是栈存在
ClearStack(s);
return OK;
}

(五)总结:和顺序栈之间的对比
对于顺序栈和链栈,其进栈和出栈的时间复杂度都是O(1).
对于空间性能,顺序栈需要事先确定一个固定长度(虽然后面可以扩展),若是这个初始长度过大,可能造成内存空间的浪费。但是他的优势是存取时定位较方便。
而链栈则需要每个元素都有指针域,这样同时也增加了一些内存开销,但是对于栈的长度无限制。
使用情况选择
如果栈的使用过程中元素变化不可预料,有时小,有时大变化频繁,那么最好是使用链栈。
若是他的变化在可控范围内,建议使用顺序栈。
注:虽然我们实现顺序栈可以扩展空间,但是当扩展后的空间无法被充分利用时,会造成空间浪费




