数据结构（二）栈与队列---栈的了解和栈的顺序存储结构和实现

（一）栈的定义

栈是一种重要的线性结构。是我们前面讲过的线性表的一种具体形式

栈是限定仅在表尾进行插入和删除操作的线性表

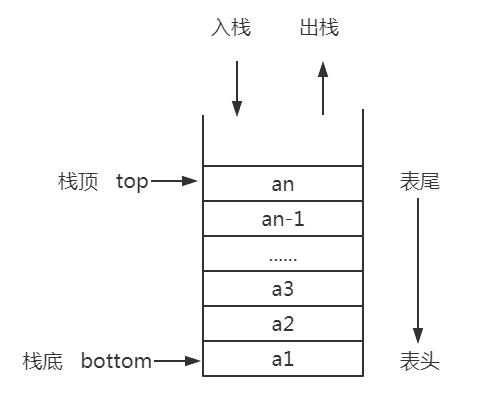
我们把允许插入和删除的一端称为栈顶top,另一端称为栈底bottom,不含任何元素的栈称为空栈。栈又称为后进先出（Last In First Out）的线性表，简称LIFO

栈的插入操作，叫做进栈，也称为压栈，入栈
栈的删除操作，叫做出栈，也称为弹栈

（二）栈的抽象数据类型

ADT 栈(stack)
Data
    同线性表。元素具有相同的类型，相邻元素具有前驱和后继的关系。

Operation
    InitStack( *s): 初始化操作，建立一个空栈
    ClearStack( *s): 将栈清空
    StackEmpty( s): 若栈存在，返回true，否则返回false
    StackLength( s): 返回栈S的元素个数

    GetTop( s, *e): 若是栈存在且非空，用e返回S的栈顶元素
    Push( *s, e):若是栈存在，则插入新的元素e到栈S中并成为栈顶元素
    Pop( *s, *e):若是栈存在且非空，删除栈顶元素，并用e返回其值
    DestroyStack( *s): 若是栈存在，则销毁他
endADT

注意：

由于栈本身就是一个线性表，那么我们讲的线性表的顺序存储和链式存储，对于栈来说，都是适用的。

（三）栈的顺序存储结构

typedef struct
{
    ElemType *base;    //栈底指针
    ElemType *top;    //栈顶指针
    int stackSize;    //最大容量，这是可修改的
}sqStack;

（四）实现栈之前的预备知识

（1）malloc函数获取的内存，内存空间上是连续的

malloc出来的空间，只是在虚拟内存中是连续的。而从实际的物理空间到虚拟内存空间还有一个映射的关系。
这个映射是由操作系统来控制的，一般情况下，从虚拟地址无法反查到物理地址。对于连续的虚拟地址空间，也就无法得知是否物理连续。
但由于映射的不确定性，当申请一段内存空间，尤其是比较大的内存长度情况下，物理地址不连续的可能性还是相当大的。
事实上，大多数的编程不需要关注物理空间是否连续。

（2）不同类型指针的步长增长问题

对于不同类型的指针，虽然指针在内存中的大小都是4字节，
但是他们的增长的地址步长与指针本身大小无关，而是与内部储存数据类型大小有关。
例如：
int *a=(int*)malloc(100*size(int))
int b,c;
b=a;
c=a++;
b=4236536 //这是10进制下的地址
c=4236540 //增长了一个int字节大小的步长

char *base = (char *)malloc(sizeof(char) * 100);
addr1 = base;
addr2 = base+1;
------------------
addr1=5350647
addr2=5350648　　//这里增长了一个char类型字节大小的步长

int *base, *top;
base = (int *)malloc(sizeof(int) * 100);
top = base + 100;
printf("size:%d\n",top - base)　　//重点：两个指针之间相减，所得到的不是地址大小之差，而是其中含有的元素个数，是100，若是我们想要知道地址之差，可以使用int强制转换十六进制地址为一个十进制数进行减法运算，结果是400

（3）指针和所指向的数据中间的关系

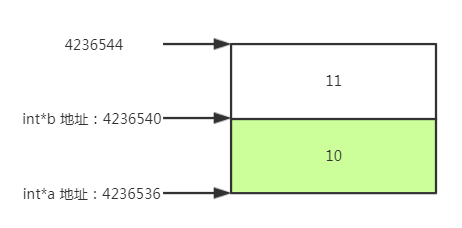
我们存储的数据在指针所指向的位置开始，占用了相关大小的字节去存放数据。
所以当我们创建栈的时候，我们的栈顶指针是不能直接读取，我们往往需要先将他降一，然后才能读取那块内存空间获取数据

例如：我们要获取栈顶数据11，我们就需要先将栈顶退一，然后才能读取到数据

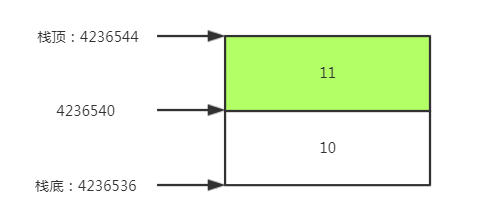
（4）realloc函数，再分配空间。用法和误区 

realloc 
       原型：extern void *realloc(void *mem_address, unsigned int newsize); 
       用法：#include <stdlib.h> 有些编译器需要#include <alloc.h> 
       功能：改变mem_address所指内存区域的大小为newsize长度。 
       说明：如果重新分配成功则返回指向被分配内存的指针，否则返回空指针NULL。 
                 当内存不再使用时，应使用free()函数将内存块释放。 
       注意：这里原始内存中的数据还是保持不变的。 

1、如果有足够空间用于扩大mem_address指向的内存块，则分配额外内存，并返回mem_address 
这里说的是“扩大”，我们知道，realloc是从堆上分配内存的，当扩大一块内存空间时， realloc()试图直接从堆上现存的数据后面的那些字节中获得附加的字节，如果能够满足，自然天下太平。也就是说，如果原先的内存大小后面还有足够的空闲空间用来分配，加上原来的空间大小＝ newsize。那么就ok。得到的是一块连续的内存。 
2、如果原先的内存大小后面没有足够的空闲空间用来分配，那么从堆中另外找一块newsize大小的内存。 
并把原来大小内存空间中的内容复制到newsize中。返回新的mem_address指针。（数据被移动了）。 
老块被放回堆上。 

注意：

1、返回值可能与ptr的值不同，如果是不同的话，那么realloc函数完成后，ptr指向的旧内存已被free掉了，会自动为我们释放，所以我们不需要关心。只需要释放新的内存地址即可
2、如果返回NULL值，则分配不成功，而原来的ptr指向的内存还没有被free掉，要求程序显式free.

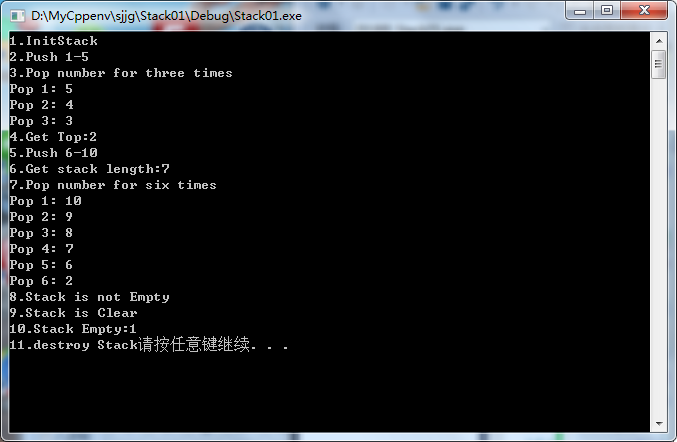
（五）栈的顺序存储结构实现

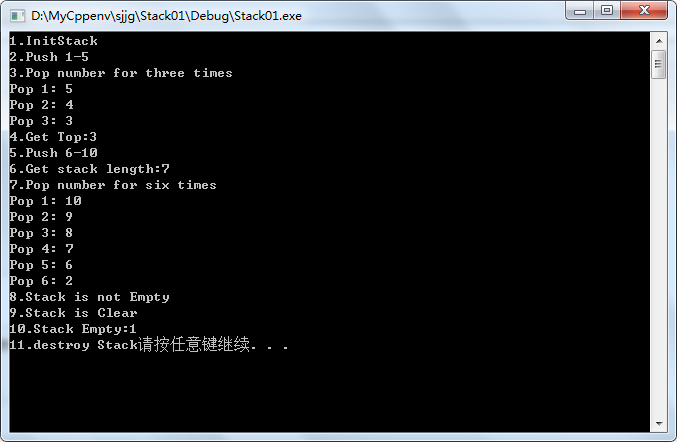
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>

#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0

#define STACK_INIT_SIZE 100    //定义栈的初始大小
#define STACK_INCR_SIZE 10    //定义栈的增长大小

typedef int ElemType;
typedef int Status;

typedef struct
{
    ElemType *base;    //栈底指针
    ElemType *top;    //栈顶指针
    int stackSize;    //最大容量，这是可修改的
}sqStack;

//四个基础操作
Status InitStack(sqStack *s);    //初始化操作，建立一个空栈
Status ClearStack(sqStack *s);    //将栈清空
Status StackEmpty(sqStack s);    //若栈存在，返回true，否则返回false
int StackLength(sqStack s);        //返回栈S的元素个数

Status GetTop(sqStack s, ElemType *e);    //若是栈存在且非空，用e返回S的栈顶元素
Status Push(sqStack *s, ElemType e);    // 若是栈存在，则插入新的元素e到栈S中并成为栈顶元素
Status Pop(sqStack *s, ElemType *e);    //若是栈存在且非空，删除栈顶元素，并用e返回其值
Status DestroyStack(sqStack *s);        //若是栈存在，则销毁他

int main()
{
    sqStack sk;
    int i;
    ElemType e;
    sk.base = sk.top = NULL;    //用于判断是否存在
    //初始化空栈
    printf("1.InitStack\n");
    InitStack(&sk);
    printf("2.Push 1-5\n");
    for (i = 1; i <= 5; i++)
        Push(&sk, i);
    printf("3.Pop number for three times\n");
    for (i = 1; i <= 3;i++)
    {
        Pop(&sk, &e);
        printf("Pop %d: %d\n",i, e);
    }
    GetTop(sk, &e);
    printf("4.Get Top:%d\n",e);
    printf("5.Push 6-10\n");
    for (i = 6; i <= 10; i++)
        Push(&sk, i);
    printf("6.Get stack length:%d\n", StackLength(sk));
    printf("7.Pop number for six times\n");
    for (i = 1; i <= 6; i++)
    {
        Pop(&sk, &e);
        printf("Pop %d: %d\n",i, e);
    }
    if (!StackEmpty(sk))
    {
        printf("8.Stack is not Empty\n");
        ClearStack(&sk);
        printf("9.Stack is Clear\n");
    }
    printf("10.Stack Empty:%d\n",StackEmpty(sk));
    printf("11.destroy Stack");
    DestroyStack(&sk);

    system("pause");
    return 0;
}

//初始化操作，建立一个空栈
Status InitStack(sqStack *s)
{
    s->base = (ElemType *)malloc(STACK_INIT_SIZE*sizeof(ElemType));
    if (!s->base)
        return ERROR;
    s->top = s->base;    //最开始，栈顶就是栈底
    s->stackSize = STACK_INIT_SIZE;
    return OK;
}

//将栈清空,将栈顶指针移动到栈底即可，容量大小不要修改，数据不需要清空，数据入栈会覆盖
Status ClearStack(sqStack *s)
{
    if (s == NULL)
        return ERROR;
    s->top = s->base;
    return OK;
}

//若栈存在，返回true，否则返回false
Status StackEmpty(sqStack s)
{
    if (s.base == s.top)
        return TRUE;
    return FALSE;
}

//返回栈S的元素个数
int StackLength(sqStack s)
{
    int length = s.top - s.base;    //指针之间运算，是按照其中数据大小字节来算的
    return length;
}

//若是栈存在且非空，用e返回S的栈顶元素,注意：只是获取栈顶数据，不出栈
Status GetTop(sqStack s, ElemType *e)
{
    if (!e || StackEmpty(s) || !s.base)
        return ERROR;
    *e = *(s.top - 1);
    return OK;
}

//入栈操作：若是栈存在，则插入新的元素e到栈S中并成为栈顶元素
Status Push(sqStack *s, ElemType e)
{
    ElemType* newStack;
    if (!s->base)
        return ERROR;

    if (s->top-s->base>=s->stackSize)    //栈满，需要再分配
    {
        newStack = (ElemType *)realloc(s->base, (s->stackSize + STACK_INCR_SIZE)*sizeof(ElemType));    //重新分配大小
        if (!newStack)    //若是分配失败，会返回NULL
        {
            free(s->base);
            exit(0);    //分配失败，直接退出
        }
        s->base = newStack;
        //分配后需要将栈顶指针进行移动到新的位置
        s->top = s->base + s->stackSize;
    }
    *(s->top) = e;
    s->top++;
    return OK;
}

//若是栈存在且非空，删除栈顶元素（只需要将栈顶指针下移即可），并用e返回其值
Status Pop(sqStack *s, ElemType *e)
{
    if (!s->base || !e || StackEmpty(*s))
        return ERROR;
    *e = *(--s->top);
    return OK;
}

//若是栈存在，则销毁他（直接将栈底指针释放即可，置为空）
Status DestroyStack(sqStack *s)
{
    if (!s->base)    //若是栈存在
    {
        s->stackSize = 0;
        free(s->base);
        s->base = s->top = NULL;
    }
    return OK;
}

（六）应用：进制转换

Status Bin2Dec(sqStack* s,int *val);    //二进制转十进制
Status Bin2Oct(sqStack* s, sqStack* sv);    //二进制转八进制
Status Bin2Hex(sqStack* s, sqStack* sv);    //二进制转十六进制

int main()
{
    sqStack sk;
    sqStack valsk;　　//接收转换为8进制或者16进制的数，需要再使用一个栈
    int dec;　　//接收转换为10进制数值
    char ch;
    ElemType e;
    sk.base = sk.top = NULL;    //用于存放二进制字符串
    valsk.base = valsk.top = NULL;    //用于存放八进制和十六进制值
    //初始化空栈
    InitStack(&sk);
    InitStack(&valsk);
    scanf("%c", &ch);
    while (ch!='#')
    {
        Push(&sk, ch);
        scanf("%c", &ch);
    }
    getchar();    //消除键盘缓冲区中的回车符

　　 //这里修改后可以测试其他进制转换，注意：转换10进制不需要用到第二个栈
    if (Bin2Hex(&sk, &valsk))
        while (!StackEmpty(valsk))
        {
            Pop(&valsk, &ch);
            printf("%c", ch);
        }

　　  DestroyStack(&sk);
　　  DestroyStack(&valsk);

    system("pause");
    return 0;
}

//二进制转十进制
Status Bin2Dec(sqStack* s, int *val)
{
    int i,key,length,v=0;
    char ch;

    if (!val || StackEmpty(*s))
        return ERROR;

    length = StackLength(*s);

    for (i = 0; i < length;i++)
    {
        Pop(s, &ch);
        key = ch - 48;
        v += key*pow(2, i);
    }
    *val = v;
    return OK;
}

//二进制转八进制
Status Bin2Oct(sqStack* s, sqStack* sv)
{
    char ord[3] = { 0 };
    char ch;
    int i,length,val;

    if (!s || !sv)
        return ERROR;

    if (!StackEmpty(*sv))
        ClearStack(sv);

    while (!StackEmpty(*s))
    {
        memset(ord, '0', 3);
        val = 0;
        length = StackLength(*s);
        if (length >= 3)
            for (i = 2; i >= 0; i--)
                Pop(s, &ord[i]);
        else
            for (i = 2; i >= 3 - length; i--)
                Pop(s, &ord[i]);

        for (i = 0; i < 3;i++)
            val += (ord[2 - i] - 48)*pow(2, i);
        Push(sv, (char)(val+48));
    }
    return OK;
}

//二进制转十六进制
Status Bin2Hex(sqStack* s, sqStack* sv)
{
    char hex[4] = { 0 };
    char ch;
    int i, length, val;

    if (!s || !sv)
        return ERROR;

    if (!StackEmpty(*sv))
        ClearStack(sv);

    while (!StackEmpty(*s))
    {
        memset(hex, '0', 4);
        val = 0;
        length = StackLength(*s);
        if (length >= 4)
            for (i = 3; i >= 0; i--)
                Pop(s, &hex[i]);
        else
            for (i = 3; i >= 4 - length; i--)
                Pop(s, &hex[i]);

        for (i = 0; i < 4; i++)
            val += (hex[3 - i] - 48)*pow(2, i);
        if (val < 10)
            Push(sv, (char)(val + 48));
        else
            Push(sv, 'A' + val - 10);

    }
    return OK;
}

（七）栈的顺序存储实现另法：使用数组

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>

#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0

#define MAXSIZE 100

typedef int ElemType;
typedef int Status;

typedef struct
{
    ElemType data[MAXSIZE];
    int top;
}sqStack;

//四个基础操作
Status InitStack(sqStack *s);    //初始化操作，建立一个空栈
Status ClearStack(sqStack *s);    //将栈清空
Status StackEmpty(sqStack s);    //若栈存在，返回true，否则返回false
int StackLength(sqStack s);        //返回栈S的元素个数

Status GetTop(sqStack s, ElemType *e);    //若是栈存在且非空，用e返回S的栈顶元素
Status Push(sqStack *s, ElemType e);    // 若是栈存在，则插入新的元素e到栈S中并成为栈顶元素
Status Pop(sqStack *s, ElemType *e);    //若是栈存在且非空，删除栈顶元素，并用e返回其值
Status DestroyStack(sqStack *s);        //若是栈存在，则销毁他

int main()
{
    sqStack sk;
    int i;
    ElemType e;

    //初始化空栈
    printf("1.InitStack\n");
    InitStack(&sk);
    printf("2.Push 1-5\n");
    for (i = 1; i <= 5; i++)
        Push(&sk, i);
    printf("3.Pop number for three times\n");
    for (i = 1; i <= 3;i++)
    {
        Pop(&sk, &e);
        printf("Pop %d: %d\n",i, e);
    }
    GetTop(sk, &e);
    printf("4.Get Top:%d\n",e);
    printf("5.Push 6-10\n");
    for (i = 6; i <= 10; i++)
        Push(&sk, i);
    printf("6.Get stack length:%d\n", StackLength(sk));
    printf("7.Pop number for six times\n");
    for (i = 1; i <= 6; i++)
    {
        Pop(&sk, &e);
        printf("Pop %d: %d\n",i, e);
    }
    if (!StackEmpty(sk))
    {
        printf("8.Stack is not Empty\n");
        ClearStack(&sk);
        printf("9.Stack is Clear\n");
    }
    printf("10.Stack Empty:%d\n",StackEmpty(sk));
    printf("11.destroy Stack");
    DestroyStack(&sk);

    system("pause");
    return 0;
}

//初始化操作，建立一个空栈
Status InitStack(sqStack *s)
{
    if (!s)
        return ERROR;
    memset(s->data, 0, MAXSIZE*sizeof(ElemType));
    s->top = -1;
    return OK;
}

//将栈清空,将栈顶指针移动到栈底即可，数据不需要清空，数据入栈会覆盖
Status ClearStack(sqStack *s)
{
    if (!s)
        return ERROR;
    s->top = -1;
    return OK;
}

//若栈存在，返回true，否则返回false
Status StackEmpty(sqStack s)
{
    if (s.top == -1)
        return OK;
    return FALSE;
}

//返回栈S的元素个数
int StackLength(sqStack s)
{
    return s.top+1;
}

//若是栈存在且非空，用e返回S的栈顶元素,注意：只是获取栈顶数据，不出栈
Status GetTop(sqStack s, ElemType *e)
{
    if (s.top = -1||!e)
        return ERROR;
    *e = s.data[s.top];
    return OK;
}

//入栈操作：若是栈存在，则插入新的元素e到栈S中并成为栈顶元素
Status Push(sqStack *s, ElemType e)
{
    if (s->top + 1 == MAXSIZE||!s)
        return ERROR;
    s->top++;
    s->data[s->top] = e;
    return OK;
}

//若是栈存在且非空，删除栈顶元素（只需要将栈顶指针下移即可），并用e返回其值
Status Pop(sqStack *s, ElemType *e)
{
    if (s->top == -1||!s||!e)
        return ERROR;
    *e = s->data[s->top];
    s->top--;
    return OK;
}

//若是栈存在，则销毁他,数据清空
Status DestroyStack(sqStack *s)
{
    if (!s)
        return ERROR;
    memset(s->data, 0, MAXSIZE*sizeof(ElemType));
    s->top = -1;
    return OK;
}

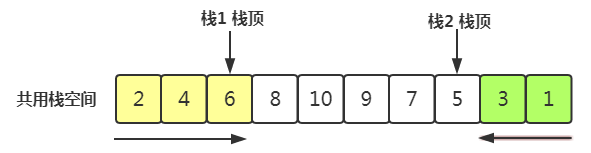
引申：两栈共享空间

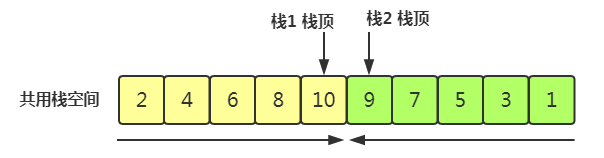
对于我们使用数组来构造顺序栈，有一个很大的缺陷，就是需要事先确定数组的存储空间大小，不够的话扩容不方便，太多了又过于浪费空间。
于是设计出来合适的大小数组，将他的空间从两头分别当做一个栈。就可以最大限度的利用数组空间。

例如：一个栈需要的空间大概为50-150，多数情况是在100以下，有少数情况会超过100。
那么当我们使用两个栈时，若是声明两个150空间的数组。则空间浪费较多。
不如一次声明200空间大小供两个栈共同使用。虽然有满栈的情况，不过出现情况不大。而且会最大程度利用了栈的空间。

 

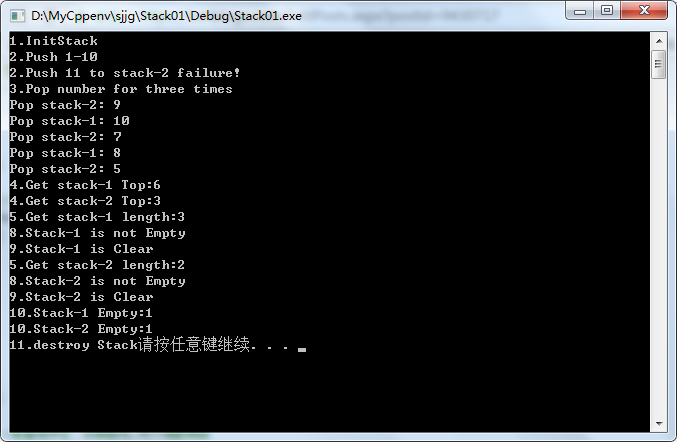
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>

#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0

#define MAXSIZE 10

typedef int ElemType;
typedef int Status;

//两栈共享空间结构
typedef struct
{
    ElemType data[MAXSIZE];
    int top1;    //栈1 栈顶指针 指向数组开始 从做向右
    int top2;    //栈2 栈顶指针 指向数组结尾 从右向左
}sqDoubleStack;

//四个基础操作
Status InitStack(sqDoubleStack *s);    //初始化操作，建立一个空栈
Status ClearStack(sqDoubleStack *s, int stackNumber);    //将栈清空
Status StackEmpty(sqDoubleStack s, int stackNumber);    //若栈存在，返回true，否则返回false
int StackLength(sqDoubleStack s, int stackNumber);        //返回栈S的元素个数

Status GetTop(sqDoubleStack s, ElemType *e, int stackNumber);    //若是栈存在且非空，用e返回S的栈顶元素
Status Push(sqDoubleStack *s, ElemType e, int stackNumber);    // 若是栈存在，则插入新的元素e到栈S中并成为栈顶元素
Status Pop(sqDoubleStack *s, ElemType *e, int stackNumber);    //若是栈存在且非空，删除栈顶元素，并用e返回其值
Status DestroyStack(sqDoubleStack *s);        //若是栈存在，则销毁他

int main()
{
    sqDoubleStack sk;
    int i;
    Status st;
    ElemType e;

    //初始化空栈
    printf("1.InitStack\n");
    InitStack(&sk);
    printf("2.Push 1-10\n");
    for (i = 1; i <= 11; i++)
    {
        st=Push(&sk, i, i % 2 + 1);
        if (st == ERROR)
            printf("2.Push %d to stack-%d failure!\n", i, i % 2 + 1);
    }
    printf("3.Pop number for three times\n");
    for (i = 1; i <= 5; i++)
    {
        Pop(&sk, &e,i%2+1);
        printf("Pop stack-%d: %d\n", i%2+1, e);
    }
    GetTop(sk, &e,1);
    printf("4.Get stack-1 Top:%d\n", e);
    GetTop(sk, &e, 2);
    printf("4.Get stack-2 Top:%d\n", e);

    printf("5.Get stack-1 length:%d\n", StackLength(sk,1));
    if (!StackEmpty(sk,1))
    {
        printf("8.Stack-1 is not Empty\n");
        ClearStack(&sk,1);
        printf("9.Stack-1 is Clear\n");
    }

    printf("5.Get stack-2 length:%d\n", StackLength(sk, 2));
    if (!StackEmpty(sk, 2))
    {
        printf("8.Stack-2 is not Empty\n");
        ClearStack(&sk, 2);
        printf("9.Stack-2 is Clear\n");
    }
    
    printf("10.Stack-1 Empty:%d\n", StackEmpty(sk,1));
    printf("10.Stack-2 Empty:%d\n", StackEmpty(sk, 2));
    printf("11.destroy Stack");
    DestroyStack(&sk);

    system("pause");
    return 0;
}

//初始化操作，建立一个空栈
Status InitStack(sqDoubleStack *s)
{
    if (!s)
        return ERROR;
    memset(s->data, 0, MAXSIZE*sizeof(ElemType));
    s->top1 = -1;
    s->top2 = MAXSIZE;
    return OK;
}

//将栈清空,stackNumber为0，两个都清空，为1清空栈1,2清空栈2
Status ClearStack(sqDoubleStack *s, int stackNumber)
{
    if (!s)
        return ERROR;
    if (stackNumber == 0)
    {
        s->top1 = -1;
        s->top2 = MAXSIZE;
    }
    else if (stackNumber==1)
    {
        s->top1 = -1;
    }
    else if (stackNumber==2)
    {
        s->top2 = MAXSIZE;
    }
    return OK;
}

//若两个栈都不存在，返回true，否则返回false
Status StackEmpty(sqDoubleStack s, int stackNumber)
{
    if (stackNumber == 0)
    {
        if (s.top1 == -1 && s.top2 == MAXSIZE)
            return OK;
    }
    else if (stackNumber == 1)
    {
        if (s.top1 == -1)
            return OK;
    }
    else if (stackNumber == 2)
    {
        if (s.top2 == MAXSIZE)
            return OK;
    }
    return FALSE;
}

//返回栈S的元素个数,是指两个栈的总长
int StackLength(sqDoubleStack s,int stackNumber)
{
    int length = 0;
    if (stackNumber == 0)
        length=(s.top1 + 1) + (MAXSIZE - s.top2);
    else if (stackNumber == 1)
        length = s.top1 + 1;
    else if (stackNumber == 2)
        length = MAXSIZE - s.top2;
    return length;
}

//若是栈存在且非空，用e返回S的栈顶元素,注意：只是获取栈顶数据，不出栈
Status GetTop(sqDoubleStack s, ElemType *e,int stackNumber)
{
    if (!e)
        return ERROR;
    if (stackNumber == 1)
        if (s.top1 == -1)
            return ERROR;
        else
            *e = s.data[s.top1];
    else if (stackNumber == 2)
        if (s.top2 == MAXSIZE)
            return ERROR;
        else
            *e = s.data[s.top2];
    return OK;
}

//入栈操作：若是栈存在，则插入新的元素e到栈S中并成为栈顶元素
Status Push(sqDoubleStack *s, ElemType e, int stackNumber)
{
    if (!s)
        return ERROR;
    if (s->top1 + 1 == s->top2)    //栈满，不允许插入
        return ERROR;
    
    if (stackNumber == 1)
        s->data[++s->top1] = e;
    else if (stackNumber==2)
        s->data[--s->top2] = e;
    
    return OK;
}

//若是栈存在且非空，删除栈顶元素（只需要将栈顶指针下移即可），并用e返回其值
Status Pop(sqDoubleStack *s, ElemType *e, int stackNumber)
{
    if (StackEmpty(*s, stackNumber)||!s || !e)
        return ERROR;
    
    if (stackNumber == 1)
        *e = s->data[s->top1--];
    else if (stackNumber==2)
        *e = s->data[s->top2++];
    return OK;
}

//若是栈存在，则销毁他,两个栈都销毁
Status DestroyStack(sqDoubleStack *s)
{
    if (!s)
        return ERROR;
    memset(s->data, 0, MAXSIZE*sizeof(ElemType));
    s->top1 = -1;
    s->top2 = MAXSIZE;
    return OK;
}

（八）两种顺序结构栈的比较

方法一的空间是malloc出来的一块连续空间，操作稍微复杂些。但是当栈满时，可以进行扩展。
方法二除了使用简单，对于栈的扩展方面欠缺。
推荐第一种，了解第二种即可

（九）栈的应用：括号匹配

对于()[]{}都是正确的[),{],(}都是匹配失败的，注意：对于引号里面的括号不进行匹配,()[]'(]'()是正确的

int main()
{
    sqStack sk;
    ElemType e;
    char ch;
    sk.base = sk.top = NULL;    //用于判断是否存在
    //初始化空栈,用于存放()[]{}''""这几个数据，的左半边进行匹配
    InitStack(&sk);
    scanf("%c", &ch);
    while (ch!='#')
    {
        if (GetTop(sk, &e))
        {
            if ((e == '"'&&ch != '"') || (e == '\''&&ch != '\''))    //若是在单双引号之间的括号全部舍去
                goto GS;
            if ((e == '"'&&ch == '"') || (e == '\''&&ch == '\''))    //匹配单双引号，优先级是最高的
            {
                Pop(&sk, &e);    //弹出单双引号
                goto GS;
            }
            if ((e == '('&&ch == ')') || (e == '['&&ch == ']') || (e == '{'&&ch == '}'))
            {
                Pop(&sk, &e);    //弹出匹配好的括号
                goto GS;
            }
            if ((ch == ')'&&e != '(') || (ch == ']'&&e != '[') || (ch == '}'&&e != '{'))    //这是当我们获取的右半边括号与栈顶不匹配时，直接退出,退出时栈不为空
                break;
        }
        else   //没有栈顶元素
        {
            if (ch == ')' || ch == ']' || ch == '}')    //没有栈顶元素时，若是我们获取的括号是右半边直接匹配失败
            {
                Push(&sk, ch);    //这里必须放一个东西入栈，以保证不为空，为一会判断做准备，至于入栈的数据随意
                break;
            }
        }
        if (ch == '('||ch=='['||ch=='{'||ch=='\'' || ch == '"')
            Push(&sk, ch);
    GS:
        scanf("%c", &ch);
    }
    getchar();
    
    if (StackEmpty(sk))
        printf("match success!");
    else
        printf("match failure!");
    system("pause");
    return 0;
}