数据结构(一)线性表链式存储实现
(一)前提
在前面的线性表顺序存储结构,最大的缺点是插入和删除需要移动大量的元素,需要耗费较多的时间。
原因:在相邻两个元素的存储位置也具有邻居关系,他们在内存中的位置是紧挨着的,中间没有间隙,当然无法快速插入和删除。
为了解决这个为题,出现了链式存储结构
(二)链式线性表两种结构(带有头结点和不带头结点)
不带头结点:
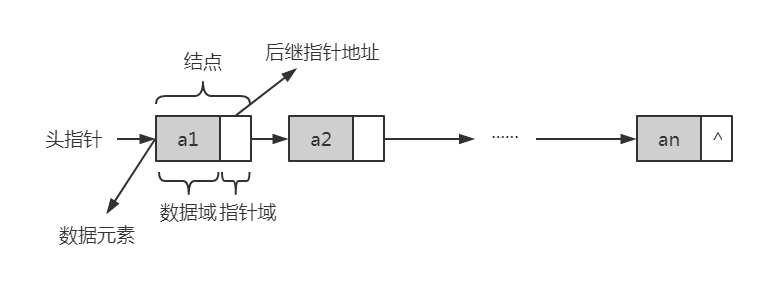
空链表:

带有头结点:

空链表:
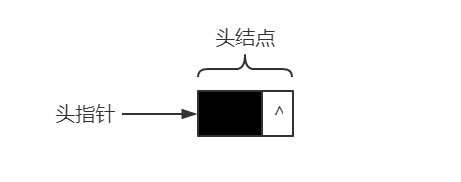
(三)头结点和头指针的区别
头指针:
1.头指针是指向第一个结点的指针,若是链表中只有头结点,则是指向头结点的指针 2.头指针具有标识作用,所以常常以头指针冠以链表的名字(指针变量名) 3.无论链表是否为空,头结点均不为空 4.头指针是链表必要元素
头结点:
1.头结点是为了操作统一和方便而设立的,放在第一个元素结点之前,其数据域一般无意义(也可以存放表长度) 2.有了头结点,对第一个元素结点的插入,删除,其操作和其他结点操作统一了 3.头结点不一定是链表的必要元素
(四)带头结点的单链表实现
#define _CRT_SECURE_NO_WARNINGS #include <stdio.h> #include <stdlib.h> #define OK 1 #define ERROR 0 #define TRUE 1 #define FALSE 0 typedef int ElemType; typedef int Status; typedef struct Node { ElemType data; struct Node* next; }Node; typedef struct Node* LinkList; //四个基本操作,初始,清空,判断是否为空,获取长度 Status InitList(LinkList* L); Status ClearList(LinkList* L); Status ListEmpty(LinkList L); int ListLength(LinkList L); //四个元素操作,插入,删除,两种查找 Status GetElem(LinkList L, int i, ElemType* e); int LocateElem(LinkList L, ElemType e); Status ListInsert(LinkList* L, int i, ElemType e); Status ListDelete(LinkList* L, int i, ElemType* e); //用来打印链表 void PrintList(LinkList L); int main() { LinkList L; ElemType e; Status ret; int i; printf("1.InitList\n"); InitList(&L); printf("2.1 Insert range of 5 elements by head\n"); for (i = 1; i <= 5;i++) { ListInsert(&L, 1, i); } printf("2.2 Insert range of 5 elements by end\n"); for (; i <= 10; i++) { ListInsert(&L, ListLength(L)+1, i); } PrintList(L); printf("3. list length:%d\n", ListLength(L)); printf("4.find element by element:%d get index:%d\n",8, LocateElem(L, 8)); GetElem(L, 6, &e); printf("5.find element by index:%d get element:%d\n",6,e); ListDelete(&L, 3, &e); printf("6.delete element by index:%d get element:%d\n",3,e); PrintList(L); printf("7.Clear\n"); ClearList(&L); printf("8.is empty:%d\n", ListEmpty(L)); system("pause"); return 0; } //四个基本操作,初始,清空,判断是否为空,获取长度 //初始化带有头结点的链表 Status InitList(LinkList* L) { *L = (LinkList)malloc(sizeof(Node)); //使头指针指向头结点 if (*L == NULL) //内存分配失败 return ERROR; (*L)->next = NULL; //指针域为空 (*L)->data = 0; //头结点数据域用来存放链表长度 return OK; } //清空链表(不会清除头结点) Status ClearList(LinkList* L) { LinkList q, p; q = (*L)->next; //是q指向第一个结点 while (q) { p = q; q = q->next; free(p); } (*L)->next = NULL; return OK; } //判断链表是否为空 Status ListEmpty(LinkList L) { if (L->next) return FALSE; return TRUE; } //获取列表长度 int ListLength(LinkList L) { /* int length=0; LinkList q=L; while (q=q->next) length++; return length; */ return L->data; } //四个元素操作,插入,删除,两种查找 //按照索引查找,获取元素 Status GetElem(LinkList L, int i, ElemType* e) { int j=1; LinkList q = L->next; while (q&&j<i) { q = q->next; j++; } if (!q || j>i) //对结果进行判断!q是没有找到数据,已经到达尾结点,j>i是针对函数输入进行判断,例如输入i=0,就不会走上面循环但是p!=null,这时节点也没有找到,就需要我们进行判断,针对这个,我们也可以在函数开始就进行长度校验,更加容易理解 return ERROR; *e = q->data; return OK; } //按照元素进行查找,获取索引 int LocateElem(LinkList L, ElemType e) { int j=0; LinkList q = L->next; while (q) { j++; if (q->data == e) break; q = q->next; } return j; } //按照索引进行插入数据 Status ListInsert(LinkList* L, int i, ElemType e) { if (L == NULL && i > (*L)->data+1) return ERROR; int j = 1; LinkList q = *L; while (q&&j<i) { q = q->next; j++; } if (i < j) return ERROR; //新建节点,加入链表 LinkList n = (LinkList)malloc(sizeof(Node)); n->data = e; n->next = q->next; q->next = n; (*L)->data++; //长度自加 return OK; } //进行元素删除 Status ListDelete(LinkList* L, int i, ElemType* e) { if (L == NULL || i>(*L)->data) return ERROR; int j=1; LinkList q, p; q = *L; while (q->next&&j<i) //这是去找指定索引元素的直接前驱 { q = q->next; j++; } if (!(q->next) || j>i) return ERROR; p = q->next; //这才是我们要删除的 *e = p->data; q->next = p->next; free(p); (*L)->data--; return OK; } //用来打印链表 void PrintList(LinkList L) { printf("begin print data:\n"); LinkList q = L->next; while (q) { printf("%d ", q->data); q = q->next; } printf("\nend print data\n"); }

1.InitList 2.1 Insert range of 5 elements by head 2.2 Insert range of 5 elements by end begin print data: 5 4 3 2 1 6 7 8 9 10 end print data 3. list length:10 4.find element by element:8 get index:8 5.find element by index:6 get element:6 6.delete element by index:3 get element:3 begin print data: 5 4 2 1 6 7 8 9 10 end print data 7.Clear 8.is empty:1 请按任意键继续. . .
注意:对于元素的插入和删除注意索引的正确与否
补充:使用头插法和尾插法创建单链表
//头插法和尾插法创建单链表 void CreateListHead(LinkList* L, int n); void CreateListEnd(LinkList* L, int n); //头插法 void CreateListHead(LinkList* L, int n) { LinkList q; //创建头结点 *L = (LinkList)malloc(sizeof(Node)); (*L)->next = NULL; (*L)->data = 0; srand(time(0)); for (int i = 0; i < n;i++) { q = (LinkList)malloc(sizeof(Node)); //创建一个新节点 q->data = rand() % 100 + 1; q->next = (*L)->next; (*L)->next = q; (*L)->data++; } } //尾插法 void CreateListEnd(LinkList* L, int n) { LinkList q, p; //创建头结点 *L = (LinkList)malloc(sizeof(Node)); (*L)->next = NULL; (*L)->data = 0; p = *L; srand(time(0)); //创建随机种子 for (int i = 0; i < n; i++) { q = (LinkList)malloc(sizeof(Node)); //创建一个新节点 q->data = rand() % 10 + 1; //进行指针交换 q->next = p->next; //这一步可以省去,但是需要在for循环后面加上p->next=NULL; p->next = q; //将p指针始终指向最后元素 p = q; //头结点数据域自增记录链表长度 (*L)->data++; } }
(五)时间复杂度的分析
单链表的查找性能为O(n)---->顺序存储结构为O(1) 单链表的插入和删除,在计算出某位置的指针后,插入和删除性能为O(1)----->顺序存储结构为O(n)
(六)空间性能分析
顺序存储结构需要预分配存储空间。
单链表不需要分配存储空间,元素限制不受控制
(七)总结
若线性表需要频繁查找,很少进行插入和删除操作,应该选择顺序存储结构。
当线性表中元素个数变化较大或者根本不知道有多大时,最好使用单链表结构,不需要考虑存储空间大小问题



