科学计算三维可视化---Mlab基础(数据可视化)
推文:科学计算三维可视化---TVTK库可视化实例
使用相关函数:科学计算三维可视化---Mlab基础(管线控制函数)
一:mlab.pipeline中标量数据可视化
通过持续实例,来感受mlab对数据可视化的方便性
(一)生成标量数据
等值面:(外层会覆盖内层)
import numpy as np from mayavi import mlab x,y,z = np.ogrid[-10:10:20j,-10:10:20j,-10:10:20j] s = np.sin(x*y*z)/(x*y*z) mlab.contour3d(s) #等值面绘制 mlab.show()

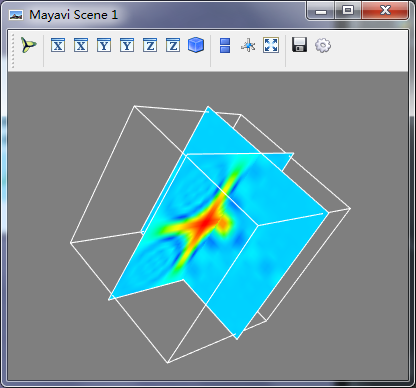
切平面:
import numpy as np from mayavi import mlab x,y,z = np.ogrid[-10:10:20j,-10:10:20j,-10:10:20j] s = np.sin(x*y*z)/(x*y*z) #绘制两个方向的切平面 mlab.pipeline.image_plane_widget(mlab.pipeline.scalar_field(s), #scalar_field获得数据的标量数据场 plane_orientation="x_axes", #设置切平面的方向 slice_index=10 ) mlab.pipeline.image_plane_widget(mlab.pipeline.scalar_field(s), plane_orientation="y_axes", slice_index=10 ) #为这个数据绘制外框 mlab.outline() mlab.show()
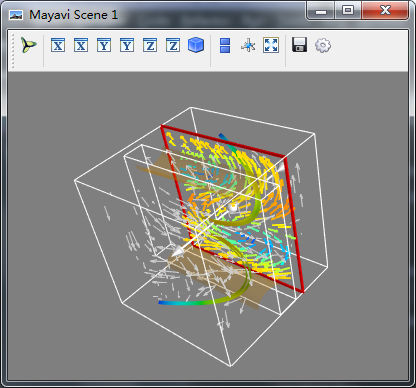
复合观测方法
import numpy as np from mayavi import mlab x,y,z = np.ogrid[-10:10:20j,-10:10:20j,-10:10:20j] s = np.sin(x*y*z)/(x*y*z) src = mlab.pipeline.scalar_field(s) #建立标量场数据 mlab.pipeline.iso_surface(src,contours=[s.min()+0.1*s.ptp(),],opacity=0.1) #iso_surface对输入体绘制其等值面,记得设置透明度,否则内部数据将被外部遮挡 mlab.pipeline.iso_surface(src,contours=[s.max()-0.1*s.ptp(),]) #也可以使用等值面iso_surface,来观察一定范围内的数据 #绘制切平面 mlab.pipeline.image_plane_widget(src, #使用切平面来观察某一平面的数据细节 plane_orientation="z_axes", #设置切平面的方向 slice_index=10 ) mlab.show()

二:mlab.pipeline中矢量数据可视化
import numpy as np from mayavi import mlab x,y,z = np.mgrid[0:1:20j,0:1:20j,0:1:20j] #u,v,w是在点x,y,z处的矢量数据 u = np.sin(np.pi*x)*np.cos(np.pi*z) v = -2*np.sin(np.pi*x)*np.cos(2*np.pi*z) w = np.cos(np.pi*x)*np.sin(np.pi*z) + np.cos(np.pi*y)*np.sin(2*np.pi*z) mlab.quiver3d(u,v,w) #quiver3d可以在数据点处画出箭头 mlab.outline() mlab.show()

上面数据过于密集:可以使用降采样:科学计算三维可视化---TVTK库可视化实例


import numpy as np from mayavi import mlab x,y,z = np.mgrid[0:1:20j,0:1:20j,0:1:20j] #u,v,w是在点x,y,z处的矢量数据 u = np.sin(np.pi*x)*np.cos(np.pi*z) v = -2*np.sin(np.pi*x)*np.cos(2*np.pi*z) w = np.cos(np.pi*x)*np.sin(np.pi*z) + np.cos(np.pi*y)*np.sin(2*np.pi*z) src = mlab.pipeline.vector_field(u,v,w) #pipeline的vectors构建了矢量域 mlab.pipeline.vectors(src,mask_points=10,scale_factor=2.0) #mask_points没10个数据点选取一个,scale_factor放缩比率2.0 mlab.show()
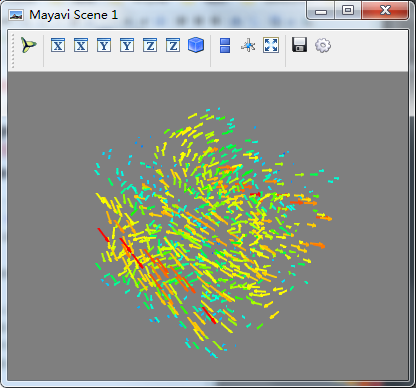
切面观察矢量数据
import numpy as np from mayavi import mlab x,y,z = np.mgrid[0:1:20j,0:1:20j,0:1:20j] #u,v,w是在点x,y,z处的矢量数据 u = np.sin(np.pi*x)*np.cos(np.pi*z) v = -2*np.sin(np.pi*x)*np.cos(2*np.pi*z) w = np.cos(np.pi*x)*np.sin(np.pi*z) + np.cos(np.pi*y)*np.sin(2*np.pi*z) src = mlab.pipeline.vector_field(u,v,w) #pipeline的vectors构建了矢量域 mlab.pipeline.vector_cut_plane(src,mask_points=10,scale_factor=2.0) #mask_points没10个数据点选取一个,scale_factor放缩比率2.0 mlab.show()
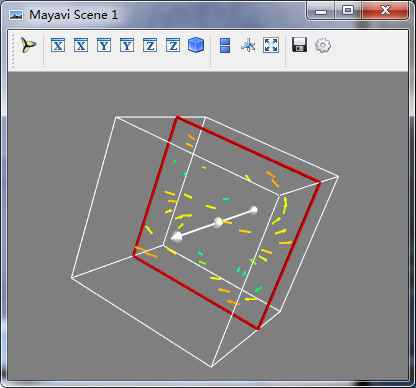
另一个矢量数据重要显示方法:级数的等值面
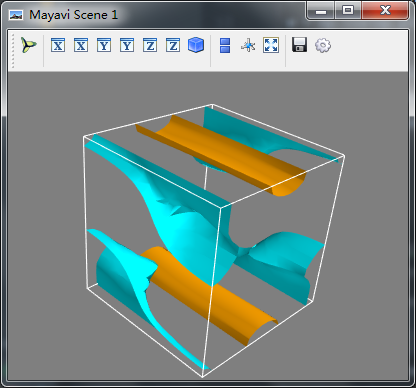
级数是矢量域中的重要参数,他可以显示数量的法线等值面,我们通过计算矢量法向得到一个标量域
import numpy as np from mayavi import mlab x,y,z = np.mgrid[0:1:20j,0:1:20j,0:1:20j] #u,v,w是在点x,y,z处的矢量数据 u = np.sin(np.pi*x)*np.cos(np.pi*z) v = -2*np.sin(np.pi*x)*np.cos(2*np.pi*z) w = np.cos(np.pi*x)*np.sin(np.pi*z) + np.cos(np.pi*y)*np.sin(2*np.pi*z) src = mlab.pipeline.vector_field(u,v,w) magnitude = mlab.pipeline.extract_vector_norm(src) #extract_vector_norm通过计算矢量法向得到一个标量域 mlab.pipeline.iso_surface(magnitude,contours=[2.0,0.5]) #构建等值面 mlab.outline() mlab.show()
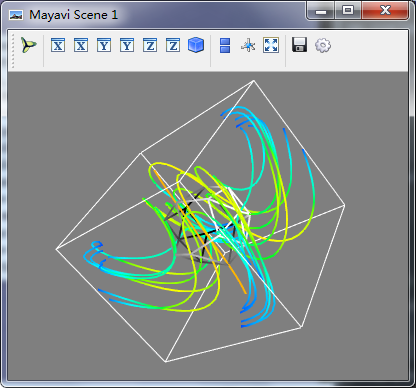
流线的可视化对矢量数据也非常有意义,在很多应用中,他可以表示流体力学的轨迹,有可以表示电磁场线
import numpy as np from mayavi import mlab x,y,z = np.mgrid[0:1:20j,0:1:20j,0:1:20j] #u,v,w是在点x,y,z处的矢量数据 u = np.sin(np.pi*x)*np.cos(np.pi*z) v = -2*np.sin(np.pi*x)*np.cos(2*np.pi*z) w = np.cos(np.pi*x)*np.sin(np.pi*z) + np.cos(np.pi*y)*np.sin(2*np.pi*z) flow = mlab.flow(u,v,w,seed_scale=1, seed_resolution=5, integration_direction="both") mlab.outline() mlab.show()
复合观测方法
为矢量场数据给出有意义的矢量观测是比较有困难的工作,因此通常我们需要使用不同的根据,对矢量数据进行可视化
#等值面 iso = mlab.pipeline.iso_surface(magnitude,contours=[2.0,],opacity=0.3) #构建等值面 #矢量场 vec = mlab.pipeline.vectors(magnitude,mask_points=40,line_width=1, color=(0.8,0.8,0.8), scale_factor=4.) #矢量场流线 flow = mlab.pipeline.streamline(magnitude,seedtype="plane", seed_visible=False, seed_scale=0.5, seed_resolution=1, linetype="ribbon") #矢量场切平面 vcp = mlab.pipeline.vector_cut_plane(magnitude,mask_points=2, scale_factor=4, colormap="jet", plane_orientation="x_axes")