参数随机初始化

转载自：https://zhuanlan.zhihu.com/p/148034113

一：参数初始化类别

参数初始化分为：固定值初始化、预训练初始化和随机初始化。

固定初始化：

是指将模型参数初始化为一个固定的常数，这意味着所有单元具有相同的初始化状态，所有的神经元都具有相同的输出和更新梯度，并进行完全相同的更新，这种初始化方法使得神经元间不存在非对称性，从而使得模型效果大打折扣。

预训练初始化：

是神经网络初始化的有效方式，比较早期的方法是使用 greedy layerwise auto-encoder 做无监督学习的预训练，经典代表为 Deep Belief Network；而现在更为常见的是有监督的预训练+模型微调。

随机初始化：

是指随机进行参数初始化，但如果不考虑随机初始化的分布则会导致梯度爆炸和梯度消失的问题。

我们这里主要关注随机初始化的分布状态。

二：Naive Initialization

先介绍两个用的比较多的初始化方法：高斯分布和均匀分布。

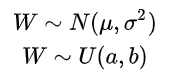
以均匀分布为例，通常情况下我们会将参数初始化为 $W\sim U(-\frac{1}{\sqrt{n}},\frac{1}{\sqrt{n}})$ ，我们来看下效果：

class MLP(nn.Module):
    def __init__(self, neurals, layers):
        super(MLP, self).__init__()
        self.linears = nn.ModuleList(
            [nn.Linear(neurals, neurals, bias=False) for i in range(layers)])
        self.neurals = neurals

    def forward(self, x):
        for (i, linear) in enumerate(self.linears):
            x = linear(x)
            print("layer:{}, std:{}".format(i+1, x.std()))
            if torch.isnan(x.std()):
                break
        return x
    
    def initialize(self):
        for m in self.modules():
            if isinstance(m, nn.Linear):
                a = np.sqrt(1/self.neurals)
                nn.init.uniform_(m.weight.data, -a, a)

neural_nums=256
layers_nums=100
batch_size=16

net = MLP(neural_nums, layers_nums)
net.initialize()

inputs = torch.randn((batch_size, neural_nums))  
output = net(inputs)

输出为：

layer:0, std:0.5743116140365601
layer:1, std:0.3258207142353058
layer:2, std:0.18501722812652588
layer:3, std:0.10656329244375229
... ...
layer:95, std:9.287707510161138e-24
layer:96, std:5.310323679717446e-24
layer:97, std:3.170952429065466e-24
layer:98, std:1.7578611563776362e-24
layer:99, std:9.757115839154053e-25

我们可以看到，随着网络层数加深，权重的方差越来越小，直到最后超出精度范围。

我们先通过数学推导来解释一下这个现象，以第一层隐藏层的第一个单元为例。

首先，我们是没有激活函数的线性网络：

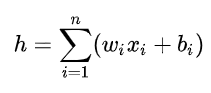
其中，n 为输入层神经元个数。

通过方差公式我们有：（x、w、b相互独立。各层的权重 w 独立同分布。且偏置项b方差为0，一般设置为常数）

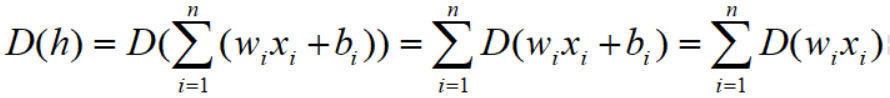
因为：

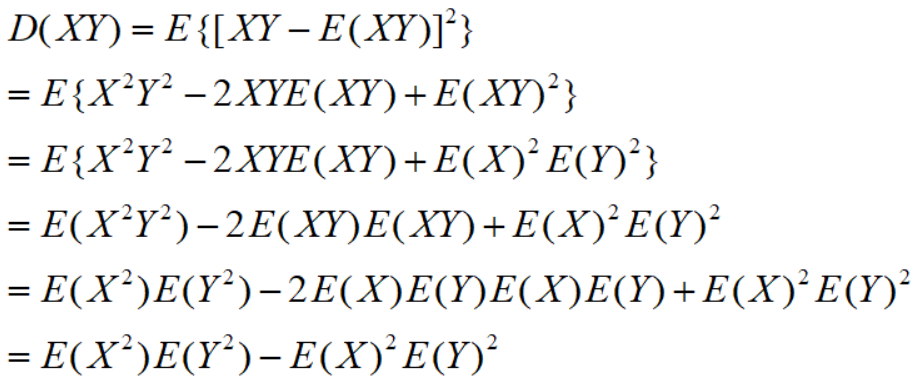
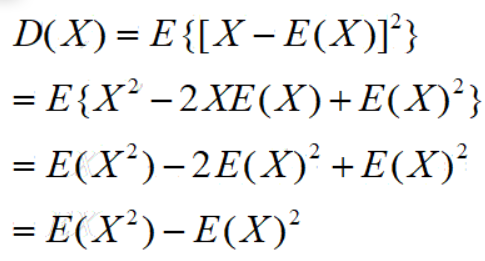
所以：

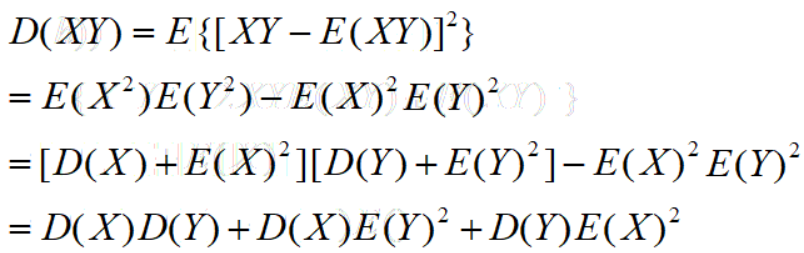
最终，方差公式有：

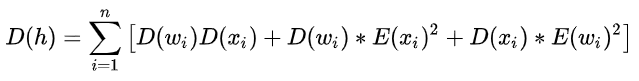
这里，我们的输入样本x均值为0，方差为1。权重w(前面提及均匀分布）的均值为0，方差为 $\frac{1}{3n}$ 。所以：

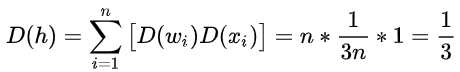
此时，神经元的标准差为 $1/\sqrt{3} \approx 0.5773$ 。

通过上式进行计算，每一层神经元的标准差都将会是前一层神经元的 $1/\sqrt{3}$ 倍。

我们可以看一下上面打印的输出，是不是正好验证了这个规律。

而这种初始化方式合理吗？有没有更好的初始化方法？

三：Xavier Initialization

Xavier Glorot 认为：优秀的初始化应该使得各层的激活值和状态梯度在传播过程中的方差保持一致。即方差一致性。

所以我们需要同时考虑正向传播和反向传播的输入输出的方差相同。

在开始推导之前，我们先引入一些必要的假设：

x、w、b 相同独立；
各层的权重 w 独立同分布，且均值为 0；
偏置项 b 独立同分布，且方差为 0；
输入项 x 独立同分布，且均值为 0；

（一）前向传播

考虑前向传播：

$h^{k} = \sum_{i=1}^{n_{k-1}} w_{i}^{k}h_i^{k-1} + b_i^{k} \\ \\$

我们令输入的方差等于输出得到方差：

$D(h^{k}) = n_{k-1} D(w^{k})D(h^{k-1}) \\$

则有：

$D(w^{k}) = 1/n_{k-1} \\ \\$

（二）反向传播

此外，我们还要考虑反向传播的梯度状态。

反向传播：

$\frac{\partial(cost)}{\partial(h^{k-1})} = \sum_{i=1}^{n_{k}}{w_i^{k}} \frac{\partial(cost)}{\partial(h_i^{k})} \\ \\$

我们也可以得到下一层的方差：

$D(w^{k}) = 1/n_{k} \\ \\$

我们取其平均，得到权重的方差为：

$D(w^{k}) = \frac{2}{n_k+n_{k-1}} \\ \\$

此时，均匀分布为：（方差逆推均匀分布）

$W\sim U(-\sqrt{\frac{6}{n_k+n_{k-1}}},\sqrt{\frac{6}{n_k+n_{k-1}}}) \\ \\$

我们来看下实验部分，只需修改类里面的初始化函数：

class MLP(nn.Module):
   ...
    def initialize(self):
        a = np.sqrt(3/self.neurals)
        for m in self.modules():
            if isinstance(m, nn.Linear):
                nn.init.uniform_(m.weight.data, -a, a)

输出结果：

layer:0, std:0.9798752665519714
layer:1, std:0.9927620887756348
layer:2, std:0.9769216179847717
layer:3, std:0.9821343421936035
...
layer:97, std:0.9224138855934143
layer:98, std:0.9622119069099426
layer:99, std:0.9693211317062378

这便达到了我们的目的，即输入和输出的方差保持一致。

（三）使用激活函数

但在实际过程中，我们还会使用激活函数，所以我们在 forward 中加入 sigmoid 函数：

class MLP(nn.Module):
  ...
    def forward(self, x):
        for (i, linear) in enumerate(self.linears):
            x = linear(x)
            x = torch.sigmoid(x)
            print("layer:{}, std:{}".format(i, x.std()))
            if torch.isnan(x.std()):
                break
        return x
    ...

再看下输出结果：（良好）

layer:0, std:0.21153637766838074
layer:1, std:0.13094832003116608
layer:2, std:0.11587061733007431
...
layer:97, std:0.11739246547222137
layer:98, std:0.11711347848176956
layer:99, std:0.11028502136468887

好像还不错，也没有出现方差爆炸的问题。

不知道大家看到这个结果会不会有些疑问：为什么方差不是 1 了？

这是因为 sigmoid 的输出都为正数，所以会影响到均值的分布，所以会导致下一层的输入不满足均值为 0 的条件。我们将均值和方差一并打出：

layer:0, mean:0.5062727928161621
layer:0, std:0.20512282848358154
layer:1, mean:0.47972571849823
layer:1, std:0.12843772768974304
...
layer:98, mean:0.5053208470344543
layer:98, std:0.11949671059846878
layer:99, mean:0.49752169847488403
layer:99, std:0.1192963495850563

可以看到，第一层隐藏层（layer 0）的均值就已经变成了 0.5。

这又会出现什么问题呢？

答案是出现 “zigzag” 现象(只有正数输出（不是zero-centered）)。https://www.zhihu.com/question/50396271?from=profile_question_card

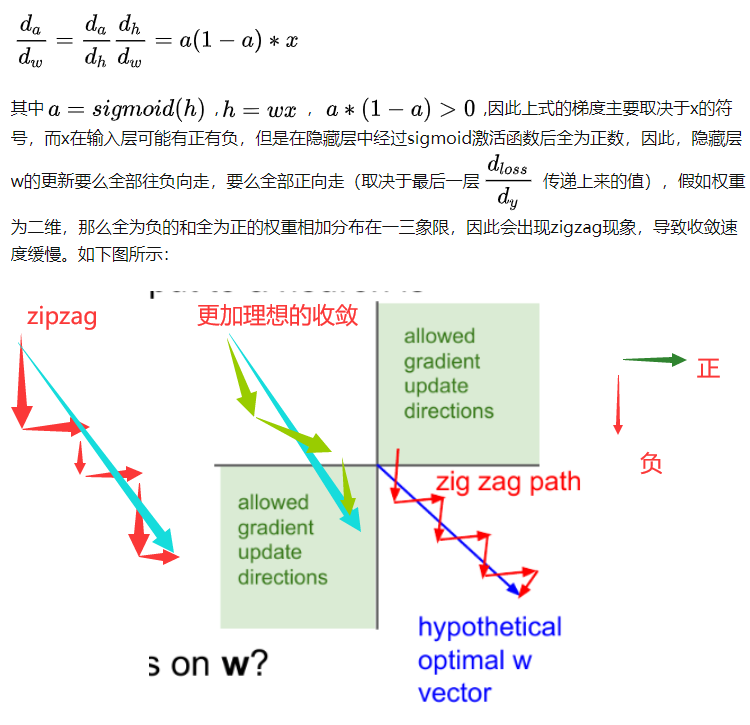
补充：对w的理解！！！

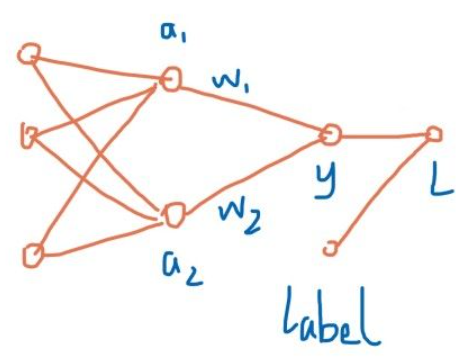
其中因为激活函数使用 sigmoid， a1>0, a2>0，对上图应用链式法则求 w1、w2偏导：

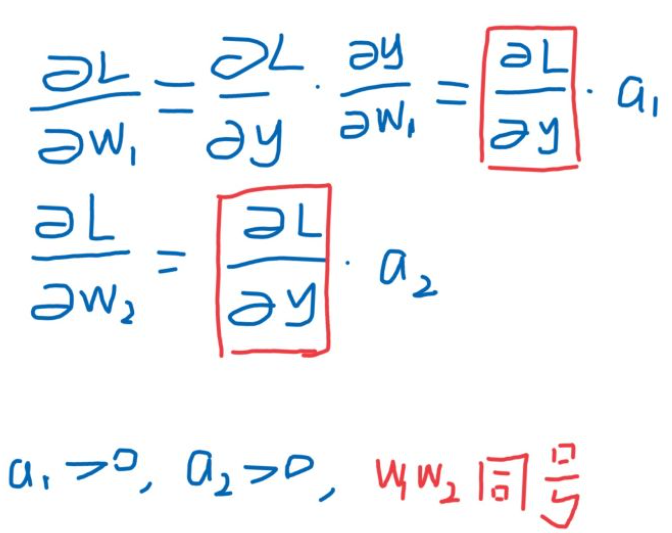
得出结论，w1、w2的梯度方向均取决于同一个值，意味着，(w1，w2）梯度必须在第一和第三象限方向移动，如果生不逢时，初始值没那么幸运，优化路径容易出现zigzag现象，汇总到 cs231 的一张ppt里，就是这样：

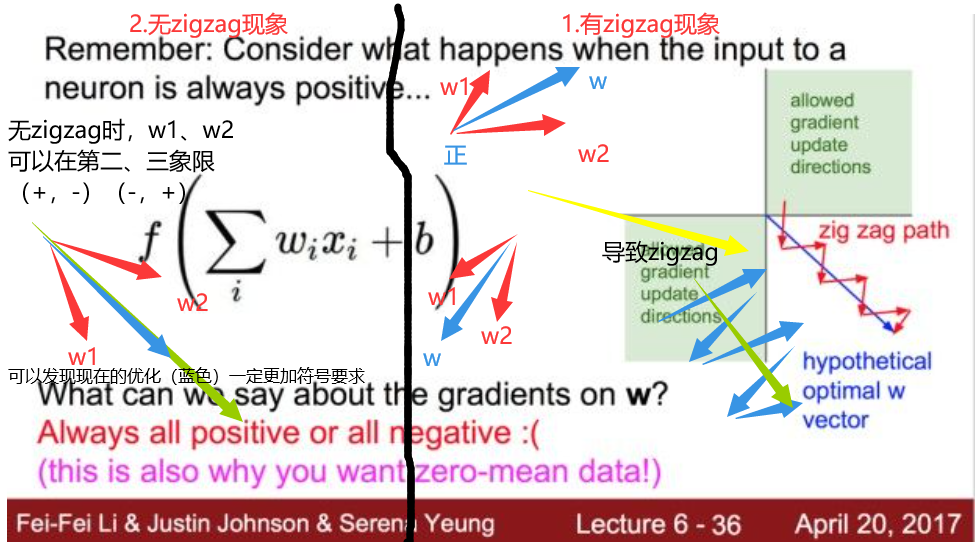
而零均值能避免 zigzag，能提高网络的训练效率。因此sigmoid 函数再效率上不如零均值的 tanh函数。

为此，我们可以使用，改变 sigmoid 的尺度与范围，改用 tanh：

$\text{tanh}(x)=2 \text{sigmoid} (2x)-1 \\ \\ \\$

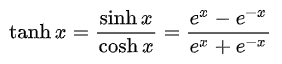
tanh 的收敛速度要比 sigmoid 快，这是因为 tanh 的均值更加接近 0，SGD 会更加接近 natural gradient，从而降低所需的迭代次数。

我们使用 tanh 做一下实验，看下输出结果：

layer:0, mean:-0.011172479018568993
layer:0, std:0.6305743455886841
layer:1, mean:0.0025750682689249516
layer:1, std:0.4874609708786011
...
layer:98, mean:0.0003803471918217838
layer:98, std:0.06665021181106567
layer:99, mean:0.0013235544320195913
layer:99, std:0.06700969487428665

可以看到，在前向传播过程中，均值没有出问题，但是方差一直在减小。

这是因为，输出的数据经过 tanh 后标准差发生了变换，所以在实际初始化过程中我们还需要考虑激活函数的计算增益：

class MLP(nn.Module):
   ...
    def initialize(self):
        for m in self.modules():
            if isinstance(m, nn.Linear):
                tanh_gain = nn.init.calculate_gain('tanh')
                a = np.sqrt(3/self.neurals)
                a *= tanh_gain
                nn.init.uniform_(m.weight.data, -a, a)

输出为：

layer:0, std:0.7603299617767334
layer:1, std:0.6884239315986633
layer:2, std:0.6604527831077576
...
layer:97, std:0.6512776613235474
layer:98, std:0.643700897693634
layer:99, std:0.6490980386734009

此时，方差就被修正过来了。

当然，在实际过程中我们也不需要自己写，可以直接调用现成的函数：

class MLP(nn.Module):
   ...
    def initialize(self):
        a = np.sqrt(3/self.neurals)
        for m in self.modules():
            if isinstance(m, nn.Linear):
                tanh_gain = nn.init.calculate_gain('tanh')
                nn.init.xavier_uniform_(m.weight.data, gain=tanh_gain)

在这里，不知道同学们会不会有一个疑问，为什么 sigmoid 不会出现 tanh 的情况呢？

这是因为 sigmoid 的信息增益为 1，而 tanh 的信息增益为 5/3。----待解决？？

tanh 和 sigmoid 有两大缺点：

需要进行指数运算；
有软饱和区域，导致梯度更新速度很慢。

所以我们经常会用到 ReLU，所以我们试一下效果：

class MLP(nn.Module):
    def __init__(self, neurals, layers):
        super(MLP, self).__init__()
        self.linears = nn.ModuleList(
            [nn.Linear(neurals, neurals, bias=False) for i in range(layers)])
        self.neurals = neurals

    def forward(self, x):
        for (i, linear) in enumerate(self.linears):
            x = linear(x)
            x = torch.relu(x)
            print("layer:{}, std:{}".format(i, x.std()))
        return x
    
    def initialize(self):
        for m in self.modules():
            if isinstance(m, nn.Linear):
                tanh_gain = nn.init.calculate_gain('relu')
                a = np.sqrt(3/self.neurals)
                a *= tanh_gain
                nn.init.uniform_(m.weight.data, -a, a)

输出为：

layer:0, std:1.4423831701278687
layer:1, std:2.3559958934783936
layer:2, std:4.320342540740967
...
layer:97, std:1.3732810130782195e+23
layer:98, std:2.3027095847369547e+23
layer:99, std:4.05964954791109e+23

为什么 Xavier 突然失灵了呢？

这是因为 Xavier 只能针对类似 sigmoid 和 tanh 之类的饱和激活函数，而无法应用于 ReLU 之类的非饱和激活函数。

针对这一问题，何凯明于 2015 年发表了一篇论文《Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification》，给出了解决方案。

在介绍 kaiming 初始化之前，这里补充下饱和激活函数的概念。

x 趋于正无穷时，激活函数的导数趋于 0，则我们称之为右饱和；
x 趋于负无穷时，激活函数的导数趋于 0，则我们称之为左饱和；
当一个函数既满足右饱和又满足左饱和时，我们称之为饱和激活函数，代表有 sigmoid，tanh；
存在常数 c，当 x>c 时，激活函数的导数恒为 0，我们称之为右硬饱和，同理左硬饱和。两者同时满足时，我们称之为硬饱和激活函数，ReLU 则为左硬饱和激活函数；
存在常数 c，当 x>c 时，激活函数的导数趋于 0，我们称之为右软饱和，同理左软饱和。两者同时满足时，我们称之为软饱和激活函数，sigmoid，tanh 则为软饱和激活函数；

四：Kaiming Initialization

同样遵循方差一致性原则。

激活函数为 $\text{ReLU}:f(x)=\text{max}(0,x)$ ，所以输入值的均值就不为 0 了，所以：

$\begin{aligned} D(h) &= n \big[ D(w_{})D(x) + D(w)*E(x)^2 + D(x)*E(w)^2 \big] \\ &= n D(w)\big[E(x)^2 + D(x) \big] \\ &= n D(w) E(x^2) \\ \end{aligned} \\ \\$

注意：这里是使用kaiming均匀分布初始化，所以E(w)=0,第一步中可以消去最后项

其中：

$\begin{aligned} E(x^{2}) &=\int_{-\infty}^{+\infty} \max (0, h)^{2} p(h) d h \\ &=\int_{0}^{+\infty} h^{2} p(h) d h \\ &=\frac{1}{2} \int_{-\infty}^{+\infty} h^{2} p(h) d h \\ &=\frac{1}{2} E\left[(h-E[h])^{2}\right] \\ &=\frac{1}{2} D(h) \end{aligned} \\ \\$

我们将其带入，可以得到：

$D(h) = n D(w) \frac{1}{2}D(h) \\ \Rightarrow D(w) = \frac{2}{n} \\ \\$

所以参数服从 $W\sim U(-\sqrt{\frac{6}{n}}, \sqrt{\frac{6}{n}})$ 。（这里注意，凯明初始化的时候，默认是使用输入的神经元个数）

我们试一下结果：

class MLP(nn.Module):
   ...    
    def initialize(self):
        a = np.sqrt(3/self.neurals)
        for m in self.modules():
            if isinstance(m, nn.Linear):
                a = np.sqrt(6 / self.neurals)
                nn.init.uniform_(m.weight.data, -a, a)

输出为：

layer:0, std:0.8505409955978394
layer:1, std:0.8492708802223206
layer:2, std:0.8718656301498413
...
layer:97, std:0.8371583223342896
layer:98, std:0.7432138919830322
layer:99, std:0.6938706636428833

可以看到，结果要好很多。

再试一下凯明均匀分布：

class MLP(nn.Module):
   ...    
    def initialize(self):
        a = np.sqrt(3/self.neurals)
        for m in self.modules():
            if isinstance(m, nn.Linear):
                nn.init.kaiming_uniform_(m.weight.data)

输出为：

layer:0, std:0.8123029470443726
layer:1, std:0.802753210067749
layer:2, std:0.758887529373169
...
layer:97, std:0.2888352870941162
layer:98, std:0.26769548654556274
layer:99, std:0.2554236054420471

那如果激活函数是 ReLU 的变种怎么办呢？

这里直接给结论：

$D(w) = \frac{2}{(1+a^2)n} \\ \\$

我们上述介绍的都是以均匀分布为例，而正态分布也是一样的。均值 0，方差也计算出来了，所服从的分布自然可知。

补充： ReLU 函数和 sigmoid 函数一样，也是非零均值的，为什么可以提高效率？

的确，使用 tanh 代替 sigmoid 就是为了提高其迭代效率，可是虽然 ReLU 也是非零均值函数，但是 ReLU 不需要求自然指数呀，因此其计算复杂度要远远小于 tanh，就算非零均值，小计算量也可以帮助 ReLU 的梯度快速收敛。总而言之，瑕不掩瑜。

不过，ReLU 函数有一个问题——在负数区硬饱和。当输入落在小于零的区间时，ReLU 函数将直接输出零，这种现象被称作Dead ReLU，但这一特性也被列入 ReLU 的优势：类似于DropOut正则化。（可以使用变种Relu)

如果不想在初始化上下功夫，可以使用Normalization，使得每一层的方差标准化。

posted @ 2020-12-17 14:34 山上有风景阅读(1205) 评论(0) 编辑收藏举报

刷新页面返回顶部

山上有风景

周围的人都比你厉害，你才会慢慢变强

参数随机初始化

转载自：https://zhuanlan.zhihu.com/p/148034113

一：参数初始化类别

参数初始化分为：固定值初始化、预训练初始化和随机初始化。

固定初始化：

预训练初始化：

随机初始化：

二：Naive Initialization

因为：

所以：

最终，方差公式有：

这里，我们的输入样本x均值为0，方差为1。权重w(前面提及均匀分布）的均值为0，方差为 $\frac{1}{3n}$ 。所以：

而这种初始化方式合理吗？有没有更好的初始化方法？

三：Xavier Initialization

（一）前向传播

（二）反向传播

此时，均匀分布为：（方差逆推均匀分布）

（三）使用激活函数

补充：对w的理解！！！

而零均值能避免 zigzag，能提高网络的训练效率。因此sigmoid 函数再效率上不如零均值的 tanh函数。

四：Kaiming Initialization

补充： ReLU 函数和 sigmoid 函数一样，也是非零均值的，为什么可以提高效率？

如果不想在初始化上下功夫，可以使用Normalization，使得每一层的方差标准化。

公告

山上有风景

周围的人都比你厉害，你才会慢慢变强

参数随机初始化

转载自：https://zhuanlan.zhihu.com/p/148034113

一：参数初始化类别

参数初始化分为：固定值初始化、预训练初始化和随机初始化。

固定初始化：

预训练初始化：

随机初始化：

二：Naive Initialization

因为：

所以：

最终，方差公式有：

这里，我们的输入样本x均值为0，方差为1。权重w(前面提及均匀分布）的均值为0，方差为 。所以：

而这种初始化方式合理吗？有没有更好的初始化方法？

三：Xavier Initialization

（一）前向传播

（二）反向传播

此时，均匀分布为：（方差逆推均匀分布）

（三）使用激活函数

补充：对w的理解！！！

而零均值能避免 zigzag，能提高网络的训练效率。因此sigmoid 函数再效率上不如零均值的 tanh函数。

四：Kaiming Initialization

补充： ReLU 函数和 sigmoid 函数一样，也是非零均值的，为什么可以提高效率？

如果不想在初始化上下功夫，可以使用Normalization，使得每一层的方差标准化。

公告

这里，我们的输入样本x均值为0，方差为1。权重w(前面提及均匀分布）的均值为0，方差为 $\frac{1}{3n}$ 。所以：